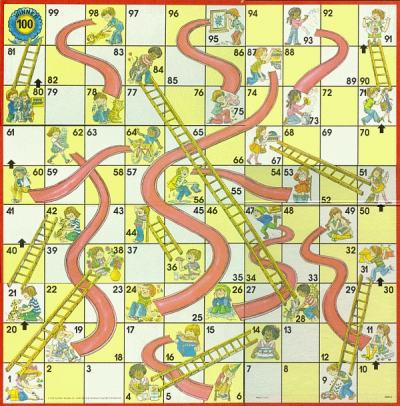
Glijbanen en ladders is een klassiek bordspel voor kinderen. Het wordt gespeeld met twee of meer spelers op een bord met 100 vakjes. De vakjes zijn genummerd van 1 tot en met 100, en zijn gerangschikt in een vierkant $$10 \times 10$$ rooster met 10 rijen en 10 kolommen. Op sommige vakjes staan glijbanen opgesteld, die een vakje verbinden met een ander vakje met een lager nummer. Op andere vakjes zijn dan weer ladders opgesteld, die een vakje verbinden met een ander vakje met een hoger nummer.
Alle spelers beginnen op het denkbeeldige vakje naast het vakje met nummer één (we zouden dit vakje 0 kunnen noemen), en gooien om de beurt met de dobbelsteen. De pion van de speler die aan de beurt is, wordt vooruit verplaatst overeenkomstig het aantal ogen op de dobbelsteen. Belandt de speler op een vakje aan de bovenkant van een glijbaan, dan glijdt de speler automatisch omlaag naar vakje aan de onderkant van de glijbaan. Komt de speler op een vakje aan de onderkant van een ladder, dan klimt de speler automatisch omhoog naar het vakje aan de bovenkant van de ladder. Als de pion na het gooien van de dobbelsteen voorbij vakje 100 zou belanden, dan blijft de pion gewoon staan en gaat de beurt naar de volgende speler. De winnaar van het spel is de speler die als eerste zijn pion op vakje 100 laat belanden.
Opgave
In deze opgave stellen we de opstelling van de glijbanen en de ladders voor als dictionaries, waarbij het nummer van het vakje aan de bovenkant van de glijbaan of aan de onderkant van de ladder als sleutel gebruikt wordt. De corresponderende waarde is telkens het number van het overeenkomstige vakje aan het andere uiteinde van de glijbaan of de ladder. Een worp met een dobbelsteen wordt aangegeven door een natuurlijk getal, dat het aantal ogen aan de bovenkant van de dobbelsteen aangeeft. Gevraagd wordt:
-
Schrijf een functie samenvoegen waaraan twee argumenten moeten doorgegeven worden, die respectievelijk de opstelling van de glijbanen en de opstelling van de ladders op het spelbord aangeven. De functie moet een nieuwe dictionary teruggeven waarvan de sleutels gevormd worden door de nummers van alle vakjes aan de bovenkant van een glijbaan of aan de onderkant van een ladder. Elke sleutel moet afgebeeld worden op een geheel getal dat aangeeft hoeveel vakjes de pion vooruit (in het geval van een ladder) of achteruit (in het geval van een glijbaan) moet gezet worden vanaf het vakje dat genummerd werd met de sleutel.
-
Gebruik de functie samenvoegen om een functie vakjes te schrijven waaraan drie argumenten moeten doorgegeven worden: i) een reeks (een lijst of een tuple) worpen, ii) de opstelling van de glijbanen op het spelbord en iii) de opstelling van de ladders op het spelbord. De functie moet een lijst teruggeven met de nummers van de vakjes waarop de pion belandt op het einde van elke beurt, als de speler de gegeven reeks van worpen gooit met de dobbelsteen. Hierbij gaan we ervan uit dat de pion zich bij aanvang bevindt op het denkbeeldige vakje naast het vakje met nummer één.
Bij de opstelling van de glijbanen en de ladders op het spelbord moeten de volgende regels in acht genomen worden:
-
een vakje mag niet tegelijkertijd het vertrekpunt zijn van een glijbaan en een ladder
-
de verplaatsing van een glijbaan moet altijd eindigen op een vakje met een lager nummer
-
de verplaatsing van een ladder moet altijd eindigen op een vakje met een hoger nummer
Indien de opstellingen van de glijbanen en de ladders die worden doorgegeven aan de functies samenvoegen en vakjes niet voldoen aan deze regels, dan moeten de functies een AssertionError opwerpen met de boodschap ongeldige opstelling. Merk op dat het dus wel toegelaten is dat een glijbaan of een ladder eindigt op een vakje waar een andere glijbaan of ladder begint. Als gevolg daarvan kan het dus zijn dat een speler zich in één beurt via meerdere glijbanen en/of ladders moet verplaatsen.
Voorbeeld
>>> glijbanen = {98: 78, 95: 75, 93: 73, 87: 24, 64: 60, 62: 19, 56: 53, 49: 11, 47: 26, 16: 6}
>>> ladders = {1: 38, 4: 14, 9: 31, 21: 42, 28: 84, 36: 44, 51: 67, 71: 91, 80: 100}
>>> samenvoegen(glijbanen, ladders)
{64: -4, 1: 37, 4: 10, 71: 20, 9: 22, 16: -10, 21: 21, 87: -63, 28: 56, 93: -20, 95: -20, 80: 20, 98: -20, 36: 8, 47: -21, 49: -38, 51: 16, 56: -3, 62: -43}
>>> glijbanen
{98: 78, 95: 75, 93: 73, 87: 24, 64: 60, 62: 19, 56: 53, 49: 11, 47: 26, 16: 6}
>>> ladders
{1: 38, 4: 14, 9: 31, 21: 42, 28: 84, 36: 44, 51: 67, 71: 91, 80: 100}
>>> samenvoegen({23: 32}, {44: 44})
Traceback (most recent call last):
AssertionError: ongeldige opstelling
>>> vakjes([1, 4, 5], glijbanen, ladders)
[38, 42, 26]
>>> vakjes([2, 4, 1, 4, 5, 5, 4, 2], glijbanen, ladders)
[2, 6, 7, 11, 6, 11, 15, 17]
>>> vakjes([5] * 16, glijbanen, ladders)
[5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 100]
>>> vakjes([6] * 14, glijbanen, ladders)
[6, 12, 18, 24, 30, 44, 50, 53, 59, 65, 91, 97, 97, 97]
>>> vakjes([4, 2, 5, 6], {23: 32}, {44: 44})
Traceback (most recent call last):
AssertionError: ongeldige opstelling
Epiloog
Het spel vindt zijn oorsprong in India, waar glijbanen in de originele versies werden voorgesteld door slangen. In het hindoeïsme staat een slang immers voor een slechte eigenschap en een ladder voor een goede eigenschap.

Het spel slangen en ladders roept heel wat interessante vragen op. Bijvoorbeeld, wat het is het minimaal aantal worpen die een speler nodig heeft om zijn pion op vakje 100 te laten belanden? Wat is het gemiddeld aantal worpen die een speler nodig heeft om zijn pion op vakje 100 te laten belanden. Of, als er $$k \geq 2$$ spelers zijn, wat is dan het gemiddeld aantal worpen die nodig zijn voordat één van de spelers vakje 100 bereikt en het spel wint? S.C. Althoen, L. King en K. Schilling bestudeerden deze en andere vragen in hun artikel "How long is a game of snakes and ladders?".