Door een catastrofale blunder in zijn boekhouding, ontdekt de paashaas pas in de vroege uurtjes van paaszondag dat hij nog snel 25 paaseieren moet gaan oprapen die verspreid liggen zoals in onderstaande rooster.
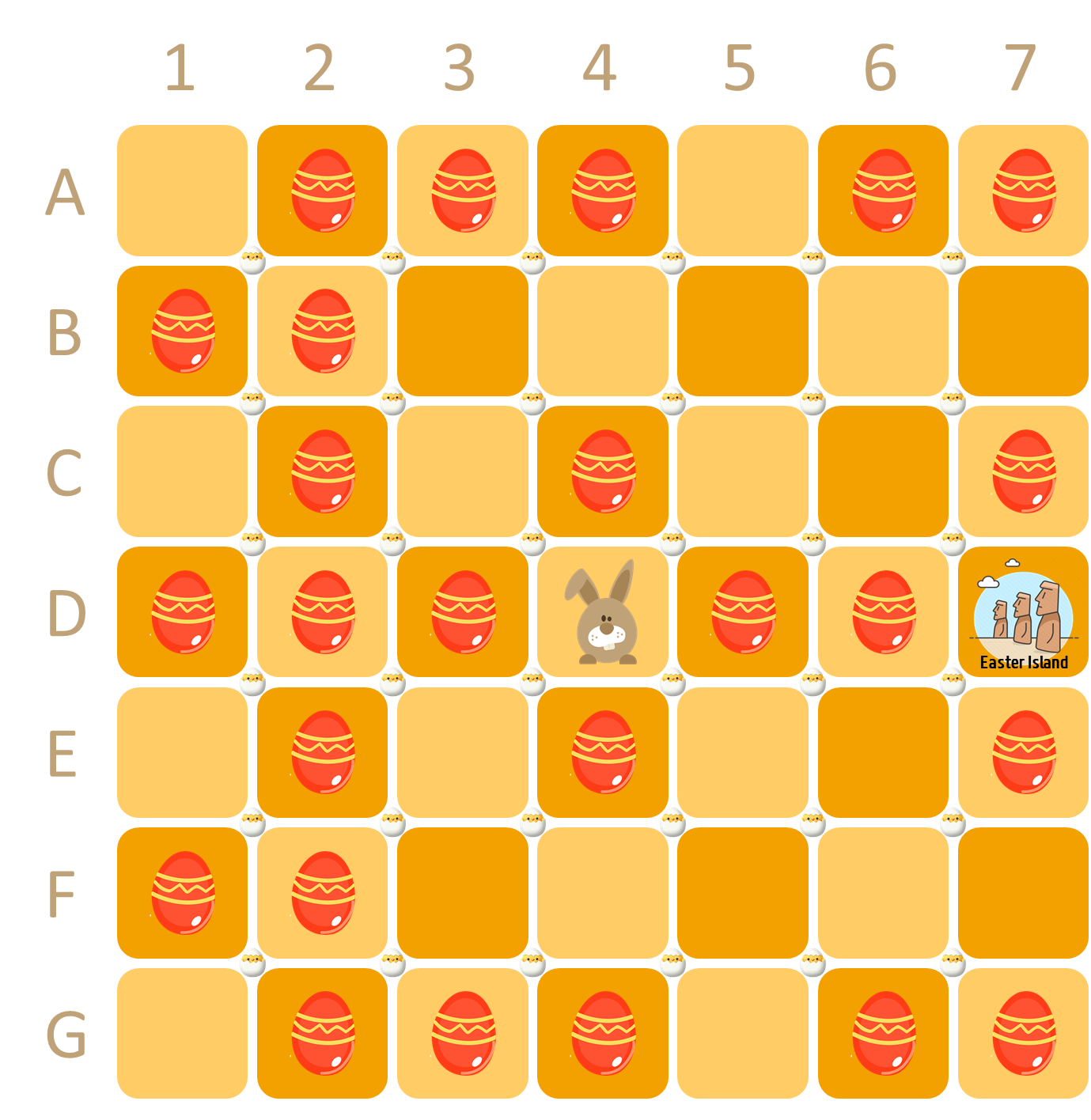
De paashaas staat aanvankelijk op positie D4. Bij elke zet moet hij naar een andere positie in het rooster springen, ofwel zoals bij een paardensprong in het schaakspel (één stap horizontaal of verticaal en twee stappen in de andere richting) of naar een positie op dezelfde rij ten oosten (rechts) van zijn huidige positie. Met andere woorden, vanaf zijn startpositie D4 (hieronder links) kan de paashaas naar elf andere posities springen: B3, B5, C2, C6, E2, E6, F3, F5, D5, D6 of D7. Als de paashaas op positie A6 stond (hieronder rechts), dan zou hij naar B4, C5, C7 of A7 kunnen springen.
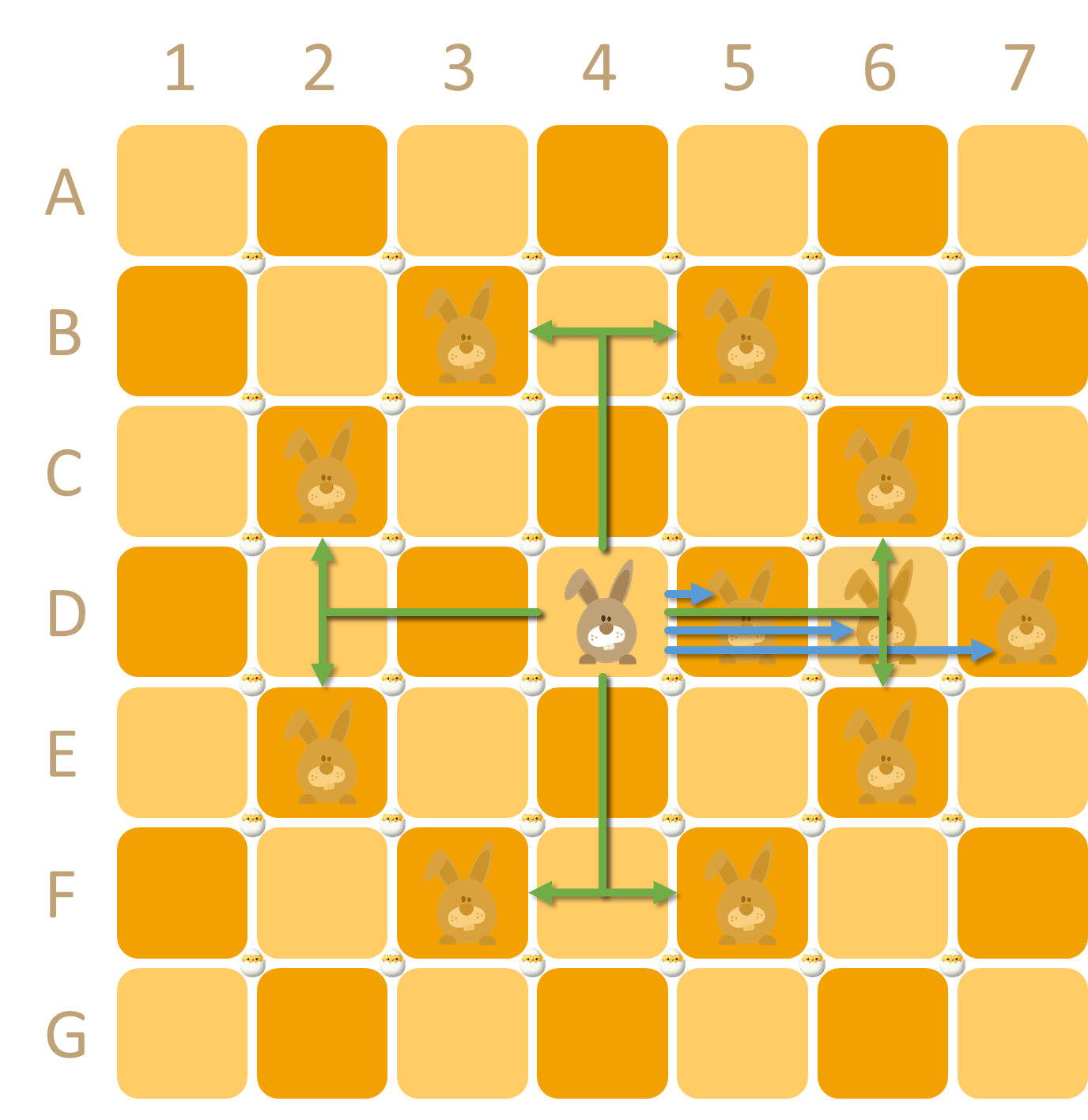
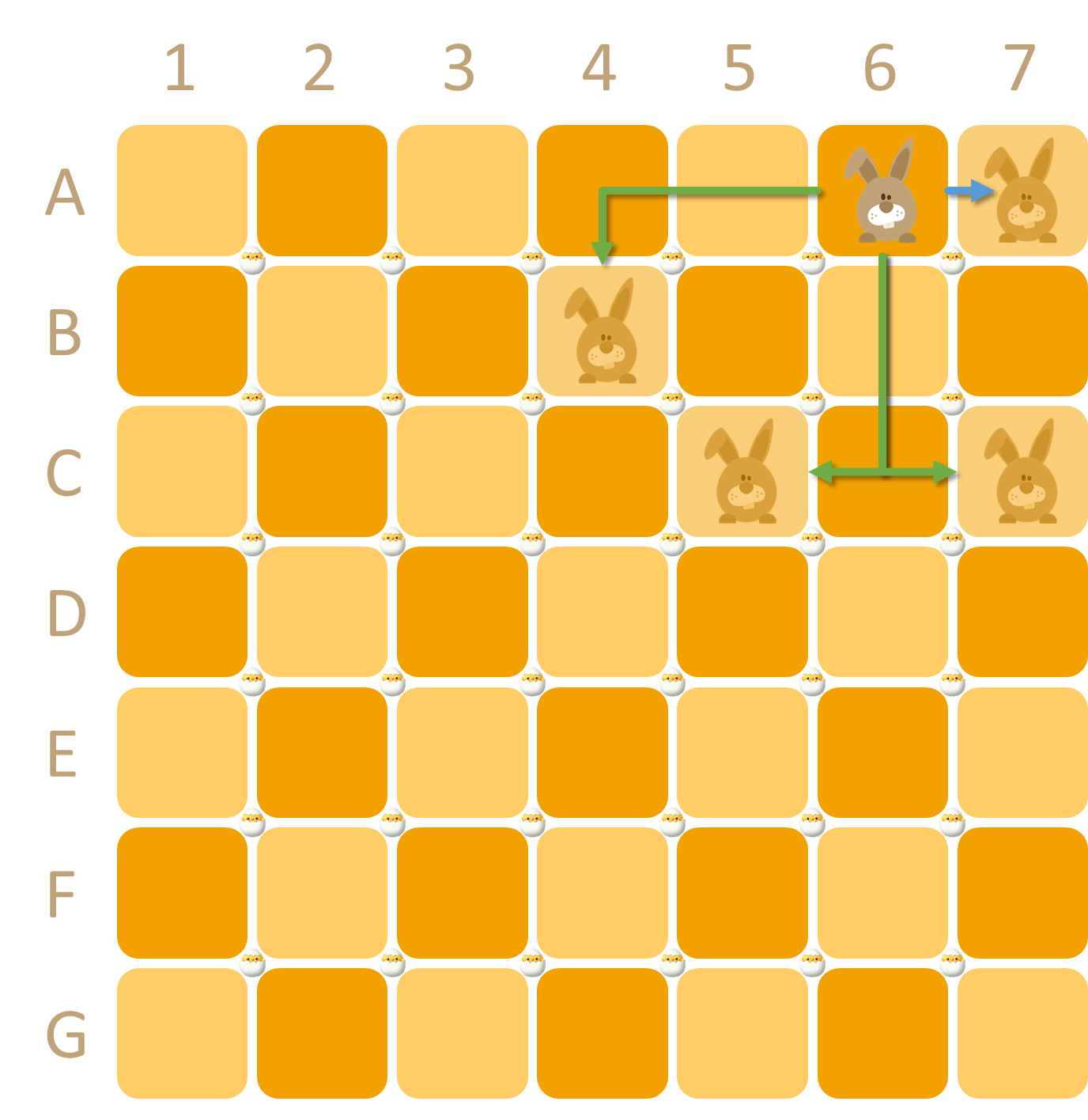
De paashaas kan enkel een paasei oprapen dat op een veld ligt waar hij naartoe springt. Als hij bijvoorbeeld in de eerste zet van D4 naar D6 zou springen, dan raapt hij enkel het paasei op positie D6 op, en niet ook het paasei op positie D5. Als gevolg daarvan kan de paashaas bij elke zet hoogstens één paasei oprapen.
Wat is het kleinste aantal zetten dat de paashaas nodig heeft om alle 25 paaseieren op te rapen en daarna terug te keren naar zijn huis op het Paaseiland1 (positie D7) — en welke route moet hij daarvoor nemen?
Opgave
De inleiding beschrijft een Easter Egg puzzel die werkt met een rechthoekig $$m \times n$$ rooster met $$m$$ rijen ($$2 \leq m \leq 26$$) en $$n$$ kolommen ($$2 \leq n \leq 26$$). De rijen van het rooster worden van boven naar onder aangeduid met de opeenvolgende hoofdletters van het alfabet. De kolommen van het rooster worden van links naar rechts genummerd vanaf 1. Daardoor kan een positie in het rooster voorgesteld worden door een string (str) die bestaat uit de hoofdletter die de rij aanduidt, gevolgd door het getal dat de kolom aanduidt.
Definieer een klasse EasterEgg waarmee het oplossen van een Easter Egg puzzel kan gesimuleerd worden. Bij het aanmaken van een nieuwe puzzel (EasterEgg) moeten vier argumenten doorgegeven worden: i) het aantal rijen $$m$$ van het rooster, ii) het aantal kolommen $$n$$ van het rooster, iii) de beginpositie van de paashaas en iv) de locatie (str) van een tekstbestand met de posities waar er aan het begin paaseieren liggen (één positie per regel). Hierbij mag je ervan uitgaan dat de argumenten een geldige startconfiguratie beschrijven, zonder dat je dit expliciet moet controleren: de paashaas en alle paaseieren bevinden zich op een positie binnen het rooster, en er ligt geen paasei op de beginpositie van de paashaas.
Als er een puzzel (EasterEgg) wordt doorgegeven aan de ingebouwde functie str, dan moet een stringvoorstelling (str) van het rooster teruggegeven worden. Daarin vormt elke rij een afzonderlijke regel, worden lege velden voorgesteld door een hekje (#), velden waarop een paasei ligt door een hoofdletter O en het veld waarop de paashaas zich bevindt door de hoofdletter X.
Daarnaast moet een puzzel (EasterEgg) minstens ook de volgende methoden ondersteunen:
-
Een methode haas waaraan geen argumenten moeten doorgegeven worden. De methode moet de huidige positie (str) van de paashaas in het rooster teruggeven.
-
Een methode eieren waaraan geen argumenten moeten doorgegeven worden. De methode moet een verzameling (set) teruggeven met de posities (str) van alle paaseieren die nog in het rooster liggen.
-
Een methode mogelijke_zetten waaraan geen argumenten moeten doorgegeven worden. De methode moet een verzameling (set) teruggeven met de posities (str) van alle velden in het rooster waarnaar de paashaas vanaf zijn huidige positie kan springen.
-
Een methode zet waaraan de positie $$p$$ (str) van een veld in het rooster moet doorgegeven worden. Als de paashaas niet vanaf zijn huidige positie naar positie $$p$$ kan springen, dan moet de paashaas blijven staan en moet de methode een AssertionError opwerpen met de boodschap ongeldige zet. Anders moet de paashaas naar positie $$p$$ springen en er het paasei oprapen als er daar één ligt (waardoor het paasei van het rooster verdwijnt), en moet de methode een verwijzing teruggeven naar het object waarop de methode werd aangeroepen.
- Een methode isleeg waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (bool) teruggeven die aangeeft of er geen paaseieren meer op het rooster liggen.
Voorbeeld
In onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand eieren.txt2 zich in de huidige directory bevindt.
>>> puzzel = EasterEgg(7, 7, 'D4', 'eieren.txt3')
>>> puzzel.haas()
'D4'
>>> puzzel.eieren()
{'A2', 'A3', 'A4', 'A6', 'A7', 'B1', 'B2', 'C2', 'C4', 'C7', 'D1', 'D2', 'D3', 'D5', 'D6', 'E2', 'E4', 'E7', 'F1', 'F2', 'G2', 'G3', 'G4', 'G6', 'G7'}
>>> print(puzzel)
#OOO#OO
OO#####
#O#O##O
OOOXOO#
#O#O##O
OO#####
#OOO#OO
>>> puzzel.isleeg()
False
>>> puzzel.mogelijke_zetten()
{'B3', 'B5', 'C2', 'C6', 'D5', 'D6', 'D7', 'E2', 'E6', 'F3', 'F5'}
>>> print(puzzel.zet('E2'))
#OOO#OO
OO#####
#O#O##O
OOO#OO#
#X#O##O
OO#####
#OOO#OO
>>> puzzel.haas()
'E2'
>>> puzzel.eieren()
{'A2', 'A3', 'A4', 'A6', 'A7', 'B1', 'B2', 'C2', 'C4', 'C7', 'D1', 'D2', 'D3', 'D5', 'D6', 'E4', 'E7', 'F1', 'F2', 'G2', 'G3', 'G4', 'G6', 'G7'}
>>> puzzel.isleeg()
False
>>> puzzel.mogelijke_zetten()
{'C1', 'C3', 'D4', 'E3', 'E4', 'E5', 'E6', 'E7', 'F4', 'G1', 'G3'}
>>> puzzel.zet('B3')
Traceback (most recent call last):
AssertionError: ongeldige zet
>>> puzzel.zet('B2')
Traceback (most recent call last):
AssertionError: ongeldige zet
>>> print(puzzel.zet('G3').zet('F1').zet('E3').zet('G2').zet('G4'))
#OOO#OO
OO#####
#O#O##O
OOO#OO#
###O##O
#O#####
###X#OO
>>> puzzel.mogelijke_zetten()
{'E3', 'E5', 'F2', 'F6', 'G5', 'G6', 'G7'}
>>> print(puzzel.zet('F2').zet('E4').zet('D2').zet('B1').zet('A3'))
#OXO#OO
#O#####
#O#O##O
O#O#OO#
######O
#######
#####OO
>>> print(puzzel.zet('C2').zet('C4').zet('B2').zet('D1').zet('D3'))
#O#O#OO
#######
######O
##X#OO#
######O
#######
#####OO
>>> print(puzzel.zet('B4').zet('A2').zet('A4').zet('A6').zet('A7'))
######X
#######
######O
####OO#
######O
#######
#####OO
>>> print(puzzel.zet('C6').zet('C7').zet('D5').zet('E7').zet('G6'))
#######
#######
#######
#####O#
#######
#######
#####XO
>>> print(puzzel.zet('G7').zet('F5').zet('D6').zet('D7'))
#######
#######
#######
######X
#######
#######
#######
>>> puzzel.isleeg()
True