Kritieke waarde

Een alternatieve wijze voor de formulering van de beslissingsregel kan worden bekomen door gebruik te maken van een kritieke waarde. In plaats van \(p\)-waarden, kan de beslissingsregel geschreven worden in termen van de teststatistiek. Bij gebruik van \(p\)-waarden bepaalt \(p=\alpha\) de grens. Een \(p\)-waarde van \(\alpha\) schrijven we als

\[p=\text{P}_0 \left[ T \leq t \right]=\alpha.\]

Dat is exact de definitie van het het \(\alpha\)-percentiel van de distributie van \(T\). In het voorbeeld is de nuldistributie \(t_{n-1}\). Dus,

\[\text{P}_0\left[T\leq -t_{n-1;\alpha}\right]=\alpha.\]

De beslissingsregel mag dus ook geschreven worden als

\[\begin{eqnarray*} \text{als } & t< -t_{n-1;\alpha} & \text{ dan verwerp }H_0\text{ en besluit }H_1 \\ \text{als } & t\geq -t_{n-1;\alpha} & \text{ dan aanvaard }H_0. \end{eqnarray*}\]

Het percentiel \(t_{n-1;\alpha}\) dat de drempelwaarde vormt in de beslissingsregel wordt in deze context de kritieke waarde op het \(5\%\) significantieniveau genoemd. De beslissingsregel waarbij de geobserveerde \(t\) vergeleken wordt met een kritieke waarde is minder algemeen geformuleerd dan deze gebruik makend van de \(p\)-waarde omdat het expliciet gebruik maakt van de nuldistributie die van teststatistiek tot teststatistiek, of zelfs van dataset tot dataset kan variëren.

De begrippen p-waarde, kritieke waarde, significantie-niveau, verwerpings- en aanvaardingsregio worden weergegeven in Figuur 21.

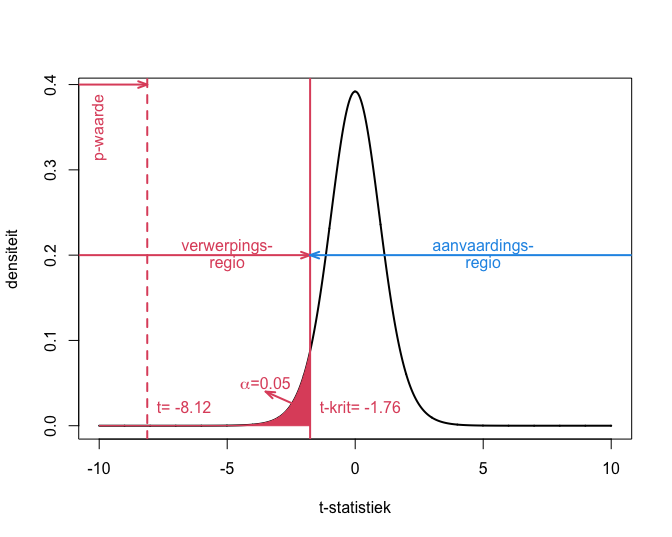
Figuur 21: Interpretatie van p-waarde, kritieke waarde, verwerpingsgebied, aanvaardingsgebied voor het captopril voorbeeld.