Associatie tussen twee continue variabelen
We zullen dit opnieuw illustreren aan de hand van de NHANES studie. We bestuderen hierbij lengte en gewicht bij vrouwen.
We voeren eerst een data exploratie uit waarbij we
- De volwassen vrouwen filteren uit de dataset
- In het ggplot commando de lengte selecteren in de x-as en het gewicht in de y-as.
- Een laag toevoegen d.m.v.
geom_pointom een scatterplot te bekomen van y i.f.v. x.
NHANES%>%
filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(x=Height,y=Weight)) +
geom_point()
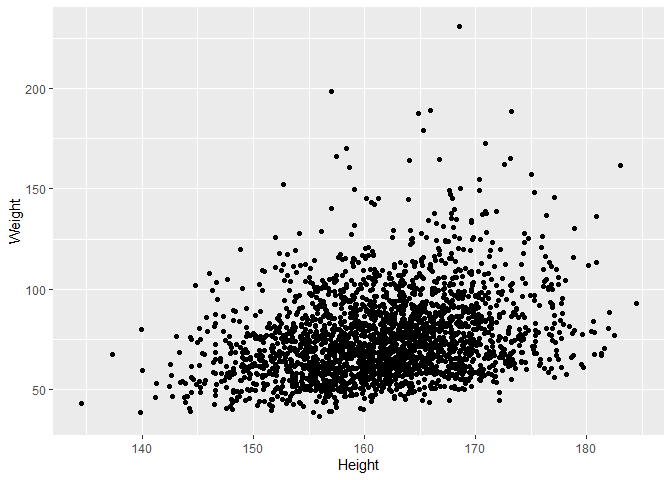
Er is een duidelijke associatie tussen gewicht en lengte: als de lengte stijgt dan stijgt het gewicht gemiddeld ook. Er is echter veel variabiliteit en ook een indicatie dat het gewicht is scheef verdeeld naar rechts.
We exploreren eerst de data univariaat: variabele per variabele. Om een
histogram en QQ-plot naast elkaar af te beelden slaan we de plots eerst
op als een object en maken we gebruik van de grid.arrange functie van
het gridExtra package om de plots naast elkaar te plotten.
p1 <- NHANES%>% filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(x=Height)) +
geom_histogram(aes(y=..density.., fill=..count..)) +
xlab("Height") +
ggtitle("All females in study") +
geom_density(aes(y=..density..))
p2 <- NHANES%>% filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(sample=Height)) +
geom_qq() +
geom_qq_line()
grid.arrange(p1,p2,ncol=2)
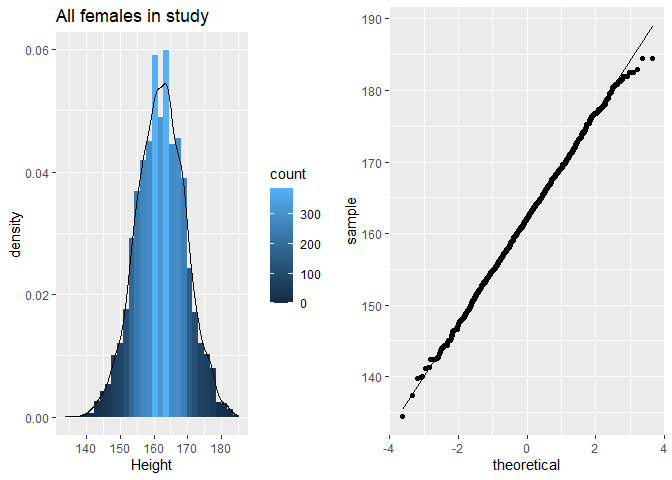
De lengte data zijn duidelijk approximatief normaal verdeeld.
p3 <- NHANES%>% filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(x=Weight)) +
geom_histogram(aes(y=..density.., fill=..count..)) +
xlab("Weight") +
ggtitle("All females in study") +
geom_density(aes(y=..density..))
p4 <- NHANES%>% filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(sample=Weight)) +
geom_qq() +
geom_qq_line()
grid.arrange(p3,p4,ncol=2)
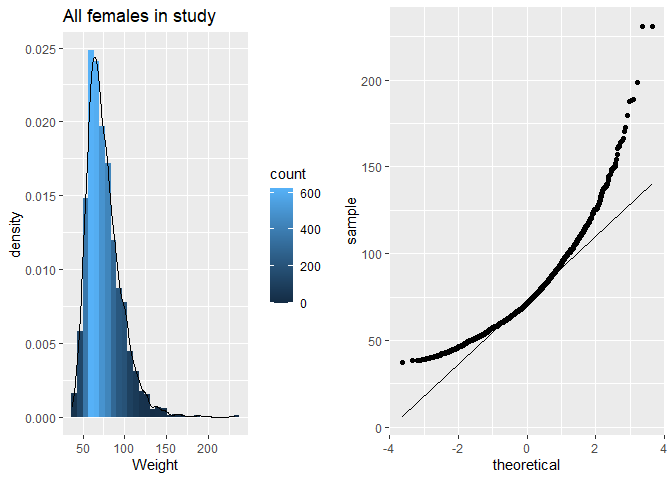
De gewichtsdata zijn inderdaad scheef verdeeld!
Na log transformatie zijn de gewichtsdata minder scheef, maar nog steeds niet Normaal verdeeld.
p5 <- NHANES%>% filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(x=Weight%>%log2)) +
geom_histogram(aes(y=..density.., fill=..count..)) +
xlab("Weight (log2)") +
ggtitle("All females in study") +
geom_density(aes(y=..density..))
p6<- NHANES%>% filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(sample=Weight%>%log2)) +
geom_qq() +
geom_qq_line()
grid.arrange(p5,p6,ncol=2)
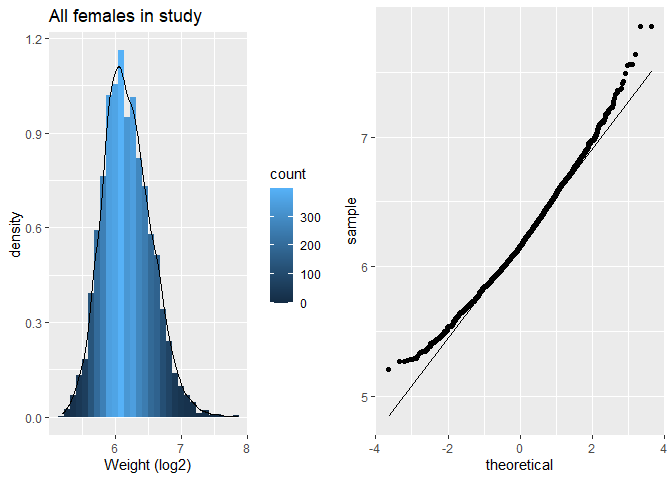
De scheefheid is er nog maar is sterk gereduceerd. We maken nu een plot van lengte in functie van het log\(_2\) getransformeerde gewicht.
NHANES%>% filter(Age >= 18 & Gender=="female") %>%
ggplot(aes(x=Height,y=Weight %>% log2)) +
ylab("Weight (log2)") +
geom_point()
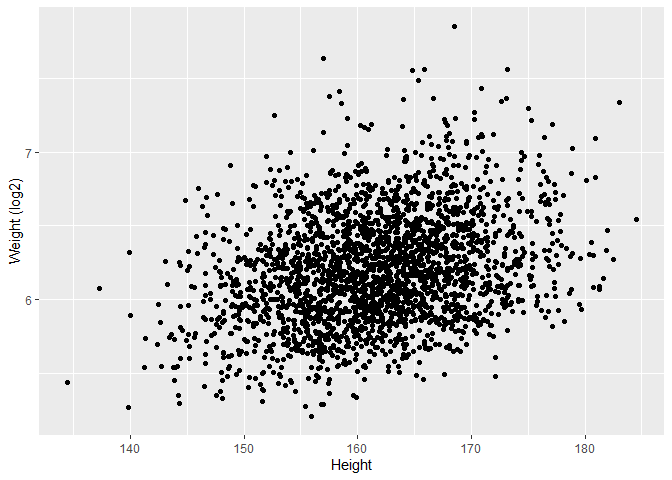
We introduceren nu een statistiek om de associatie te schatten: de correlatie.