Kies een willekeurig getal $$n \in \mathbb{N}$$. Vorm een nieuw getal $$n'$$ door de cijfers van het getal $$n$$ van achter naar voor te schrijven. Bereken de som $$n + n'$$ van deze twee getallen.

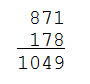
In de meeste gevallen zal het herhalen van deze procedure uiteindelijk een palindroom opleveren:

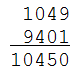
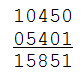
Op de één of andere perverse manier geldt dit echter niet voor het getal 196 — althans, computersimulaties die de procedure herhaald hebben tot getallen van meer dan 300 miljoen cijfers lang, hebben nooit een palindroom gevonden. Is 196 immuun voor het genereren van palindromen? Tot nu toe heeft niemand een sluitend bewijs voor of tegen weten te leveren, dus voorlopig kent niemand nog het antwoord op deze vraag.

Opgave

Een palindroom is een woord, zin, getal of andere reeks karakters die hetzelfde lezen van links naar rechts als van rechts naar links. De term palindroom werd in de 17e eeuw geïntroduceerd door de Engelse schrijver Ben Johnson¹, en is een samenstelling van de Griekse woorden palin (πάλιν, "opnieuw") en dromos (δρóμος, "weg, richting").

• Schrijf een functie palindroom waaraan een string moet doorgegeven worden. De functie moet een Booleaanse waarde teruggeven die aangeeft of de gegeven string al dan niet een palindroom is. Bij het bepalen of de string symmetrisch is, moet de functie standaard rekening houden met alle karakters en moet de functie ook onderscheid maken tussen hoofdletters en kleine letters. De functie heeft echter ook nog drie optionele parameters die dit gedrag kunnen wijzigen. Aan deze parameters kan telkens een Booleaanse waarde doorgegeven worden, die standaard ingesteld is op True. De optionele parameters hebben de volgende naam, volgorde, en betekenis:

• cijfers: als de waarde False wordt doorgegeven aan deze parameter, moet de functie alle cijfers in de gegeven string negeren

• andere: als de waarde False wordt doorgegeven aan deze parameter, moet de functie alle karakters in de gegeven string negeren die geen letter of cijfer zijn

• hoofdlettergevoelig: als de waarde False wordt doorgegeven aan deze parameter, moet de functie geen onderscheid maken tussen hoofdletters en kleine letters

• Gebruik de functie palindroom om een functie hardnekkig te schrijven, waaraan een getal $$n \in \mathbb{N}$$ moet doorgegeven worden. De functie moet teruggeven hoeveel keer de hierboven beschreven procedure moet uitgevoerd worden, alvorens een getal bekomen wordt dat een palindroom is. Omdat er getallen bestaan waarvoor de procedure naar alle waarschijnlijkheid nooit een palindroom oplevert, heeft de functie ook een optionele parameter maximum waaraan een getal $$m \in \mathbb{N}$$ (standaardwaarde: 1000) kan doorgegeven worden. Indien de functie na $$m$$ herhalingen nog geen palindroom heeft opgeleverd, moet de functie de waarde $$m$$ als resultaat teruggeven.

Voorbeeld

>>> palindroom('a1b2c3c2b1a')
True
>>> palindroom('a1b2c3C2B1A')
False
>>> palindroom('a1b2c3C2B1A', hoofdlettergevoelig=False)
True
>>> palindroom('a1b2c3c4b5a')
False
>>> palindroom('a1b2c3c4b5a', cijfers=False)
True

>>> palindroom('step on no pets')
True
>>> palindroom('Step on no pets')
False
>>> palindroom('Step on no pets', hoofdlettergevoelig=False)
True
>>> palindroom("No 'x' in 'Nixon'", andere=False, hoofdlettergevoelig=False)
True

>>> hardnekkig(871)
3
>>> hardnekkig(196)
1000
>>> hardnekkig(196, maximum=200)
200
>>> hardnekkig(78552)
31
>>> hardnekkig(78552, maximum=25)
25