We saw that ridge regression with a wise choice of \(\lambda\) can outperform least squares as well as the null model on the Hitters data set. We now ask whether the lasso can yield either a more accurate or a more interpretable model than ridge regression. In order to fit a lasso model, we once again use the glmnet() function; however, this time we use the argument alpha=1. Other than that change, we proceed just as we did in fitting a ridge model.

lasso.mod <- glmnet(x[train,], y[train], alpha = 1, lambda = grid)
plot(lasso.mod)

plot

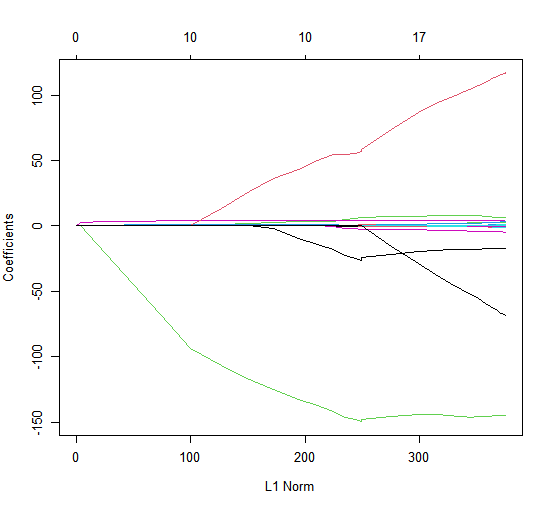
We can see from the coefficient plot that depending on the choice of tuning parameter, some of the coefficients will be exactly equal to zero. We now perform cross-validation and compute the associated test error.

> set.seed(1)
> cv.out <- cv.glmnet(x[train,], y[train], alpha = 1)
> plot(cv.out)
> bestlam <- cv.out$lambda.min
> lasso.pred <- predict(lasso.mod, s = bestlam, newx = x[test,])
> mean((lasso.pred - y.test)^2)
[1] 143673.6

plot

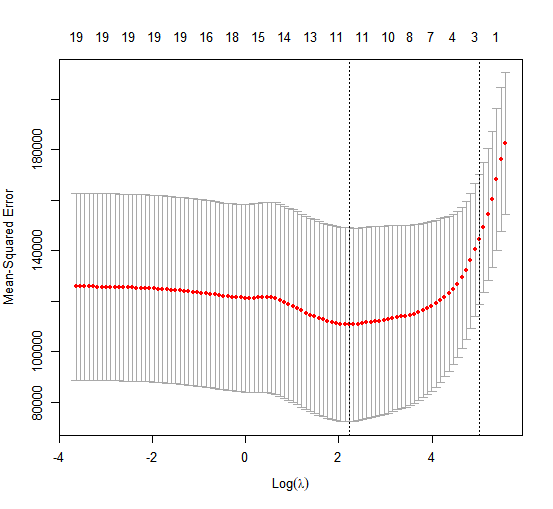
This is substantially lower than the test set \(MSE\) of the null model and of least squares, and very similar to the test \(MSE\) of ridge regression with \(\lambda\) chosen by cross-validation.

However, the lasso has a substantial advantage over ridge regression in that the resulting coefficient estimates are sparse. Here we see that 12 of the 19 coefficient estimates are exactly zero. So the lasso model with \(\lambda\) chosen by cross-validation contains only seven variables.

> out <- glmnet(x, y, alpha = 1, lambda = grid)
> lasso.coef <- predict(out, type = "coefficients", s = bestlam)[1:20,]
> lasso.coef
  (Intercept)         AtBat          Hits         HmRun 
   1.27479059   -0.05497143    2.18034583    0.00000000 
         Runs           RBI         Walks         Years 
   0.00000000    0.00000000    2.29192406   -0.33806109 
       CAtBat         CHits        CHmRun         CRuns 
   0.00000000    0.00000000    0.02825013    0.21628385 
         CRBI        CWalks       LeagueN     DivisionW 
   0.41712537    0.00000000   20.28615023 -116.16755870 
      PutOuts       Assists        Errors    NewLeagueN 
   0.23752385    0.00000000   -0.85629148    0.00000000 
> lasso.coef[lasso.coef != 0]
  (Intercept)         AtBat          Hits         Walks 
   1.27479059   -0.05497143    2.18034583    2.29192406 
        Years        CHmRun         CRuns          CRBI 
  -0.33806109    0.02825013    0.21628385    0.41712537 
      LeagueN     DivisionW       PutOuts        Errors 
  20.28615023 -116.16755870    0.23752385   -0.85629148

Using the Boston dataset, try determining the lambda that minimizes the \(MSE\) (store it in bestlam) using the cross-validation approach (store the cross-validation output in cv.out). With the acquired \(\lambda\), create a Lasso Regression model lasso.mod with bestlam as the lambda parameter, then determine the lasso regression predictions (store them in lasso.pred) and calculate the \(MSE\) (store it in lasso.mse).

Assume that: