Weerstanden zijn passieve elektrische componenten met twee aansluitingen. Ze bemoeilijken de doorgang van elektrische stroom. In elektronische schakelingen worden weerstanden gebruikt om de stroomsterkte te verminderen, signaalniveaus aan te passen, spanningen te verdelen en transmissielijnen te beëindigen.

Om de sterkte van een weerstand aan te duiden, wordt gebruikgemaakt van de elektronische kleurcode (huidige internationale standaard: IEC 60062:20161). Hierbij worden drie, vier of vijf gekleurde banden op de weerstand aangebracht. Bij reparaties van gemonteerde weerstanden bleek het immers niet altijd eenvoudig om de gedrukte tekst te lezen op deze kleine componenten, zeker als de bedrukte kant niet goed zichtbaar was omdat ze tegen het chassis of een andere component lag. Gekleurde banden hebben echter ook hun nadelen, zeker voor personen met kleurenblindheid. Oververhitting of vervuiling van een weerstand kunnen er ook voor zorgen dat bruin moeilijk te onderscheiden valt van rood of oranje.
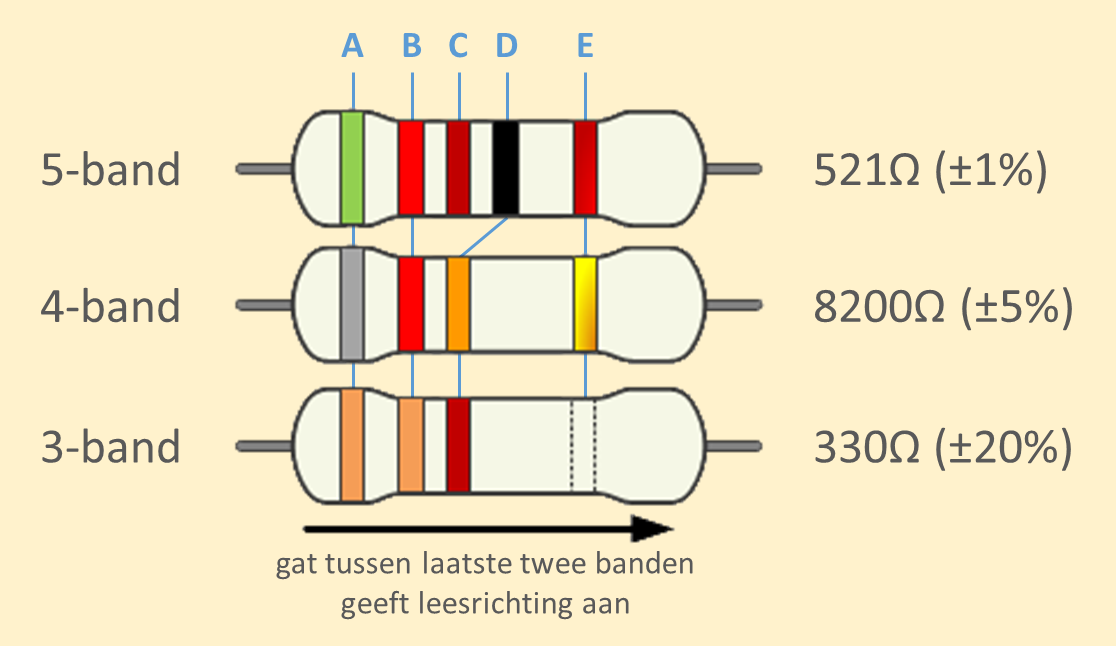
Om onderscheid te maken tussen links en rechts wordt er een breder gat gelaten tussen de voorlaatste (C/D) en de laatste (E) band. De sterkte van de weerstand wordt als volgt gecodeerd door de gekleurde banden:
-
band A is het eerste significante cijfer van de sterkte
-
band B is het tweede significante cijfer van de sterkte
-
band C is het derde significante cijfer van de sterkte (deze band is optioneel)
-
band D is de decimale vermenigvuldigingsfactor
-
band E geeft procentueel de nauwkeurigheid van de sterkte aan (deze band is optioneel)
De IEC 60062:20162 standaard schrijft de volgende kleurcodes voor:
| kleur | significant cijfer | vermenigvuldigingsfactor | nauwkeurigheid (%) |
|---|---|---|---|
| (geen) | - | - | 20 |
| PINK | - | $$\times 10^{-3}$$ | - |
| SILVER | - | $$\times 10^{-2}$$ | 10 |
| GOLD | - | $$\times 10^{-1}$$ | 5 |
| BLACK | 0 | $$\times 10^{0}$$ | - |
| BROWN | 1 | $$\times 10^{1}$$ | 1 |
| RED | 2 | $$\times 10^{2}$$ | 2 |
| ORANGE | 3 | $$\times 10^{3}$$ | - |
| YELLOW | 4 | $$\times 10^{4}$$ | - |
| GREEN | 5 | $$\times 10^{5}$$ | 0.5 |
| BLUE | 6 | $$\times 10^{6}$$ | 0.25 |
| VIOLET | 7 | $$\times 10^{7}$$ | 0.1 |
| GRAY | 8 | $$\times 10^{8}$$ | 0.05 |
| WHITE | 9 | $$\times 10^{9}$$ | - |
De kleuren zijn net als in een regenboog gerangschikt volgens het spectrum van zichtbaar licht: rood (2), oranje (3), geel (4), groen (5), blauw (6) en violet (7). Zwart (0) heeft geen energie, bruin (1) heeft er een klein beetje meer, wit (9) heeft alles en grijs (8) is net zoals wit, maar dan een beetje minder intens. Lee Sallows ontwierp deze vernuftige regenboogtabel op basis van de elektronische kleurcode:

De tabel beeldt de letters in de bovenste rij af op de getallen 1, 2, …, 9 en de letters in de onderste rij op de getallen -1, -2, …, -9. Het geniale zit in het feit dat de toekenning van waarden aan letters zo gebeurt dat als we de waarden van alle letters optellen in de naam van elke kleur uit de elektronische code, de som overeenkomt met het significante cijfer dat die kleur voorstelt in de standaard. Op die manier vormt de tabel een soort omgebogen regenboog.
| B+L+A+C+K | = | -4+7+6-7-2 | = | 0 |
| B+R+O+W+N | = | -4+9-9+8-3 | = | 1 |
| R+E+D | = | +9-1-6 | = | 2 |
| O+R+A+N+G+E | = | -9+9+6-3+1-1 | = | 3 |
| Y+E+L+L+O+W | = | -8-1+7+7-9+8 | = | 4 |
| G+R+E+E+N | = | +1+9-1-1-3 | = | 5 |
| B+L+U+E | = | -4+7+4+1 | = | 6 |
| V+I+O+L+E+T | = | +3+5-9+7-1+2 | = | 7 |
| G+R+A+Y | = | +1+9+6-8 | = | 8 |
| W+H+I+T+E | = | +8-5+5+2-1 | = | 9 |
Opgave
De waarde van een woord (int) is een geheel getal dat bekomen wordt door de waarden van de individuele letters van het woord bij elkaar op te tellen. De waarde van een letter (int) wordt bepaald aan de hand van een reeks met $$2n$$ letters ($$n \in \mathbb{N}_0$$), die achtereenvolgens de waarde $$-n, \ldots, -2, -1, 1, 2, \ldots, n$$ hebben (let hierbij op het feit dat nul ontbreekt). Bij het bepalen van de woordwaarde wordt geen onderscheid gemaakt tussen hoofdletters en kleine letters.
Aan alle functies uit deze opgave moet een reeks (str, list of tuple) met een even aantal verschillende letters (str) doorgegeven worden. Als dit argument geen reeks is met een even aantal letters waarin geen enkele letter meermaals voorkomt (hierbij mag geen onderscheid gemaakt worden tussen hoofdletters en kleine letters), dan moet een AssertionError opgeworpen worden met de boodschap ongeldige letters. Het opwerpen van deze AssertionError krijgt telkens voorrang op andere exceptions die eventueel door de functies opgeworpen worden.
Voorts wordt aan sommige functies een woord (str) of een reeks (list of tuple) met woorden (str) doorgegeven. Deze functies moeten expliciet controleren dat elk woord een string is die enkel bestaat uit letters die voorkomen in de gegeven reeks letters (hierbij mag geen onderscheid gemaakt worden tussen hoofdletters en kleine letters). Als dat niet het geval is, dan moet een AssertionError opgeworpen worden met de boodschap ongeldig woord.
Gevraagd wordt:
-
Schrijf een functie letterwaarde waaraan een reeks met een even aantal verschillende letters moet doorgegeven worden. De functie moet een dictionary (dict) teruggeven die elke letter (str) uit de gegeven reeks afbeeldt op zijn corresponderende waarde (int). De sleutels van deze dictionary moeten allemaal hoofdletters zijn.
-
Schrijf een functie woordwaarde waaraan twee argumenten moeten doorgegeven worden: een woord (str) en een reeks met een even aantal verschillende letters. De functie moet de woordwaarde (int) van het gegeven woord teruggeven, waarbij de waarde van de letters bepaald wordt op basis van de gegeven reeks letters.
-
Schrijf een functie regenboog waaraan twee argumenten moeten doorgegeven worden: een reeks met $$m \in \mathbb{N}$$ woorden en een reeks met een even aantal verschillende letters. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of de woorden in de gegeven reeks achtereenvolgens woordwaarde $$0, 1, \ldots, m - 1$$ hebben. Hierbij moet de woordwaarde bepaald worden aan de hand van de gegeven reeks letters.
-
Schrijf een functie omgebogen waaraan twee argumenten moeten doorgegeven worden: een reeks woorden en een reeks met een even aantal verschillende letters. De functie moet een tuple teruggeven waarin de woorden uit de gegeven reeks volgens oplopende woordwaarde gerangschikt zijn. Hierbij moet de woordwaarde bepaald worden aan de hand van de gegeven reeks letters. Woorden met dezelfde woordwaarde moeten alfabetisch gerangschikt worden, zonder daarbij onderscheid te maken tussen hoofdletters en kleine letters.
De functies mogen de argumenten die eraan doorgegeven worden nooit wijzigen.
Voorbeeld
>>> letterwaarde('OYCDHBNKEgtvuialwr')
{'O': -9, 'Y': -8, 'C': -7, 'D': -6, 'H': -5, 'B': -4, 'N': -3, 'K': -2, 'E': -1, 'G': 1, 'T': 2, 'V': 3, 'U': 4, 'I': 5, 'A': 6, 'L': 7, 'W': 8, 'R': 9}
>>> letterwaarde('abc')
Traceback (most recent call last):
AssertionError: ongeldige letters
>>> letterwaarde('abba')
Traceback (most recent call last):
AssertionError: ongeldige letters
>>> woordwaarde('black', 'OYCDHBNKEGTVUIALWR')
0
>>> woordwaarde('BROWN', 'oycdhbnkeGTVUIALWR')
1
>>> woordwaarde('red', 'OYCDHBNKEgtvuialwr')
2
>>> woordwaarde('SILVER', 'OYCDHBNKEGTVUIALWR')
Traceback (most recent call last):
AssertionError: ongeldig woord
>>> regenboog(['BLACK', 'brown', 'RED', 'orange', 'YELLOW', 'green', 'BLUE', 'violet', 'GRAY', 'White'], 'OYCDHBNKEgtvuialwr')
True
>>> regenboog(['BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown'], 'OYCDHBNKEgtvuialwr')
False
>>> regenboog(('BLACK', 'brown', 'RED', 'orange', 'YELLOW', 'green', 'BLUE', 'violet', 'GRAY', 'White'), 'bwdiucankYOGTHELRV')
False
>>> kleuren = ['BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown']
>>> omgebogen(kleuren, 'OYCDHBNKEgtvuialwr')
('BLACK', 'brown', 'RED', 'orange', 'YELLOW', 'green', 'BLUE', 'violet', 'GRAY', 'White')
>>> kleuren
['BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown']
>>> kleuren = ('BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown')
>>> omgebogen(kleuren, 'bwdiucankYOGTHELRV')
('BLACK', 'brown', 'BLUE', 'White', 'RED', 'GRAY', 'orange', 'YELLOW', 'green', 'violet')