Een flatgebouw heeft een plat dak met afmetingen $$3^k \times 3^k$$ ($$k \in \mathbb{N_0}$$) meter en zijden parallel met noordzuidelijke en oostwestelijke richtingen. Het dak is bedekt met vierkante tegels die zijden hebben van 1 meter. Eén van de tegels werd echter verwijderd, waardoor een gat in het dak is ontstaan dat groot genoeg is om erdoor te vallen. De tegels vormen een vierkant rooster op het dak, waardoor hun posities kunnen aangeduid worden aan de hand van $$(x, y)$$-coördinaten. De tegel in de zuidwestelijke hoek heeft coördinaten $$(1, 1)$$. De eerste coördinaat neemt toe als we in oostelijke richting gaan, en de tweede coördinaat neemt toe als we naar het noorden gaan.
Op het dak van het gebouw doolt een slaapwandelaar rond, die telkens wandelt naar een naburige tegel ten oosten (O), westen (W), zuiden (Z) of noorden (N) van de tegel waarop hij staat. De tocht van de slaapwandelaar start op de tegel in de zuidwestelijke hoek van het dak. Het traject dat de slaapwandelaar aflegt kan omschreven worden als een woord $$d_k$$ dat enkel opgebouwd is uit de letters N, Z, O en W die respectievelijk een stap naar het noorden, zuiden, oosten en westen aangeven. Voor $$k = 1$$ wordt het traject omschreven door het woord
$$d_1$$ = OONNWZWN
Voor $$k = 2$$ wordt het traject van de slaapwandelaar omschreven door het woord
| $$d_2$$ = | NNOOZWZOONNOOZWZOOOONNWZWNNOONNWZWNNOONN |
| WZWNWWWZZONOZZZZWWNONWWZZWWNONWNOONNWZWN |
Onderstaande afbeelding geeft het traject weer dat door een slaapwandelaar gevolgd wordt op een dak met afmetingen van $$3 \times 3$$ (links) en $$9 \times 9$$ (rechts).
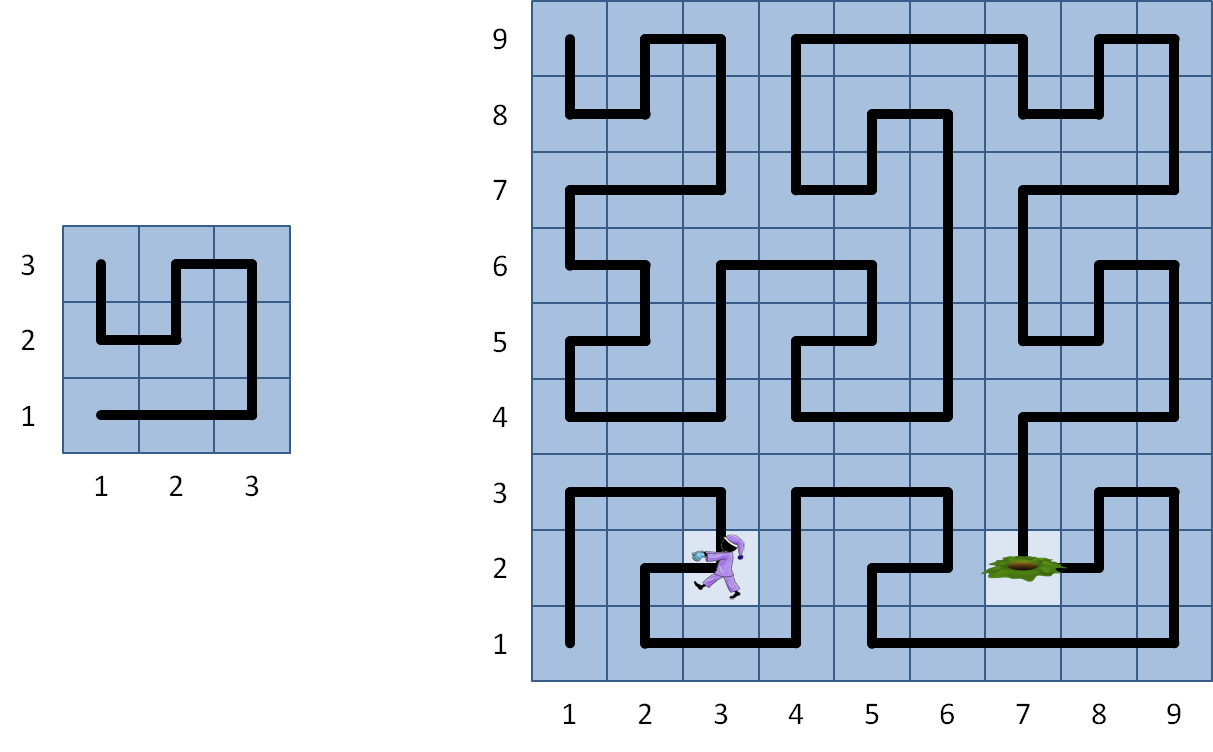
In het algemene geval wordt het traject van een slaapwandelaar op een dak met afmetingen $$3^{k+1} \times 3^{k+1}$$ voor $$k \geq 1$$ omschreven door het woord
$$d_{k + 1}$$ = $$p_a(d_k)$$ O $$p_a(d_k)$$ O $$d_k$$ N $$d_k$$ N $$d_k$$ W $$p_c(d_k)$$ Z $$p_b(d_k)$$ W $$p_b(d_k)$$ N $$d_k$$
waarbij de functies $$p_a$$, $$p_b$$ en $$p_c$$ de
volgende permutaties van de richtingen aangeven
| O | W | N | Z | |
|---|---|---|---|---|
| $$p_a$$ | N | Z | O | W |
| $$p_b$$ | Z | N | W | O |
| $$p_c$$ | W | O | Z | N |
We hebben dan bijvoorbeeld dat $$p_a$$(ZON) = WNO, $$p_b$$(ZON) = OZW en $$p_c$$(ZON) = NWZ.
Opgave
We beginnen de slaapwandelaar te observeren op het ogenblik dat hij zich op de tegel met coördinaten $$(s_x, s_y)$$ bevindt. De vraag is hoeveel stappen de slaapwandelaar erover zal doen om in het gat te vallen dat ontstaan is doordat de tegel met coördinaten $$(g_x, g_y)$$ werd verwijderd. Om deze vraag te beantwoorden ga je als volgt te werk
Schrijf een functie permutatie waaraan twee stringargumenten moeten doorgegeven worden. Het eerste argument moet een woord met richtingen voorstellen (een string die enkel bestaat uit de letters N, Z, O en W). Het tweede argument is ofwel de letter a, b, of c. Deze letter geeft aan of de functie permutatie respectievelijk het resultaat van de permutatie $$p_a$$, $$p_b$$ of $$p_c$$ moet teruggeven.
Schrijf een functie traject waaraan een getal $$k \in \mathbb{N_0}$$ als argument moet doorgegeven worden. De functie moet een string als resultaat teruggeven, die het woord met richtingen voorstelt dat een slaapwandelaar aflegt op een dak met afmetingen $$3^k \times 3^k$$.
Schrijf een functie slaapwandelaar die bepaalt hoeveel stappen een slaapwandelaar erover zal doen om in het gat te vallen. Aan deze functie moeten vijf argumenten doorgegeven worden. Het eerste argument is een getal $$k \in \mathbb{N_0}$$ op basis waarvan de afmeting van het dak ($$3^k \times 3^k$$) bepaald wordt. De volgende twee argumenten stellen respectievelijk de coördinaten $$s_x$$ en $$s_y$$ voor van de tegel waarop de slaapwandelaar zich bevindt bij de start van de observatie. De laatste twee argumenten stellen respectievelijk de coördinaten $$g_x$$ en $$g_y$$ voor van de tegel die werd verwijderd.
Voorbeeld
>>> permutatie('ZON', 'a')
'WNO'
>>> permutatie('ZON', 'b')
'OZW'
>>> permutatie('ZON', 'c')
'NWZ'
>>> traject(1)
'OONNWZWN'
>>> traject(2)
'NNOOZWZOONNOOZWZOOOONNWZWNNOONNWZWNNOONNWZWNWWWZZONOZZZZWWNONWWZZWWNONWNOONNWZWN'
>>> route = traject(3)
>>> print('\\n'.join(route[x:x + 80] for x in range(0, len(route), 80)))
OONNWZWNNOONNWZWNNNNOOZWZOONNOOZWZOONNOOZWZOZZZWWNONWWWWZZONOZZWWZZONOZONNOOZWZO
OOONNWZWNNOONNWZWNNNNOOZWZOONNOOZWZOONNOOZWZOZZZWWNONWWWWZZONOZZWWZZONOZONNOOZWZ
OONNOOZWZOONNOOZWZOOOONNWZWNNOONNWZWNNOONNWZWNWWWZZONOZZZZWWNONWWZZWWNONWNOONNWZ
WNNNNOOZWZOONNOOZWZOOOONNWZWNNOONNWZWNNOONNWZWNWWWZZONOZZZZWWNONWWZZWWNONWNOONNW
ZWNNNNOOZWZOONNOOZWZOOOONNWZWNNOONNWZWNNOONNWZWNWWWZZONOZZZZWWNONWWZZWWNONWNOONN
WZWNWZZWWNONWWZZWWNONWWWWZZONOZZWWZZONOZZWWZZONOZOOONNWZWNNNNOOZWZOONNOOZWZOZWWZ
ZONOZZWWZZONOZZWWZZONOZZZZWWNONWWZZWWNONWWZZWWNONWNNNOOZWZOOOONNWZWNNOONNWZWNWZZ
WWNONWWWWZZONOZZWWZZONOZZZZWWNONWWZZWWNONWWZZWWNONWNNNOOZWZOOOONNWZWNNOONNWZWNWZ
ZWWNONWNNNOOZWZOONNOOZWZOOOONNWZWNNOONNWZWNNOONNWZWNWWWZZONOZZZZWWNONWWZZWWNONWN
OONNWZWN
>>> slaapwandelaar(2, 3, 2, 7, 2)
20
>>> slaapwandelaar(2, 9, 6, 3, 7)
43
>>> slaapwandelaar(3, 1, 1, 1, 27)
728