Het schiereiland Manhattan vormt één van de vijf stadsdelen van New York. Dit stadsdeel staat bekend om zijn wolkenkrabbers, brede avenues, het financiële centrum Wall Street en de vele, gele taxi's die er rondrijden. De straten van Manhattan zijn ingedeeld volgens het rechthoekige Commissioners' Plan van 1811. Het gebied wordt doorsneden door avenues (noord-zuid) en streets (oost-west).

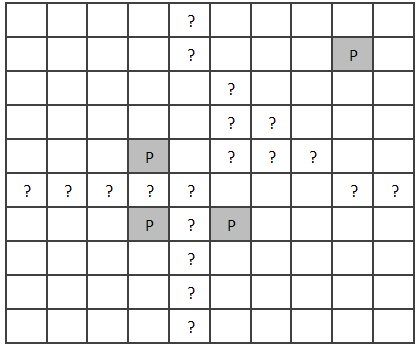
Veronderstel een gegeven rechthoekig $$s \times a$$ rooster dat een deelgebied van Manhattan met $$s$$ streets en $$a$$ avenues voorstelt. Op verschillende kruispunten zijn pompstations te vinden waar taxi's kunnen tanken. Wanneer een taxi zonder benzine dreigt te vallen, kan de chauffeur op zijn GPS de coördinaten van het dichtsbijzijnde pompstation aflezen. Er is echter een bug in de software van de GPS geslopen. Als er vanaf een kruispunt meerdere "dichtste" pompstations zijn, dan raakt de GPS het noorden kwijt, waardoor de chauffeur in paniek slaat en een aanrijding veroorzaakt. Dergelijke kruispunten worden daarom ook dode punten genoemd.

Opgave

In Manhattan wordt een kruispunt (verder kortweg punt genoemd) op een rechthoekig $$s \times a$$ rooster steeds voorgesteld als een tuple $$(x, y)$$, waarbij $$x, y \in \mathbb{N}$$, $$0 \leq x < s$$ en $$0 \leq y < a$$. Het punt in de linkerbovenhoek van het rooster is dus het punt $$(0, 0)$$, en het punt in de rechteronderhoek is het punt $$(s-1, a-1)$$. Dit is ook de voorstelling van punten zoals die in deze opgave gebruikt worden.

• In Manhattan wordt de afstand tussen twee kruispunten $$(x_1, y_1)$$ en $$(x_2, y_2)$$ berekend als \[|x_1 - x_2| + |y_1 - y_2|\,,\]waarbij $$|x|$$ de absolute waarde van $$x$$ voorstelt. Deze afstand wordt immers niet voor niets de Manhattan-afstand (of city block distance) genoemd. Schrijf een functie manhattanAfstand die de Manhattan-afstand tussen twee gegeven kruispunten als resultaat teruggeeft. De coördinaten van de twee punten moeten als argument aan de functie doorgegeven worden.

• Gebruik de functie manhattanAfstand om een functie doodpunt te schrijven die een Booleaanse waarde teruggeeft die aangeeft of een gegeven kruispunt een dood punt is of niet. Aan deze functie moeten twee argumenten doorgegeven worden: de coördinaten van het kruispunt waarvoor moet bepaald worden of het al dan niet een dood punt is, en een lijst van punten die de locaties van de pompstations op het $$s \times a$$ rooster aangeven.

• Schrijf een functie manhattan waaraan drie argumenten moeten doorgegeven worden: het aantal streets $$s$$, het aantal avenues $$a$$, en een lijst van punten die de locaties van de pompstations op het $$s \times a$$ rooster aangeven. De functie moet een voorstelling van het rechthoekig rooster uitschrijven, waarbij kruispunten worden aangeduid met een sterretje (*). Kruispunten waarop een pompstation gelegen is moeten echter voorgesteld worden met de letter P, en kruispunten die dode punten zijn moeten voorgesteld worden met de letter D.

Voorbeeld

In het voorbeeld $$10\times 10$$ rooster dat in onderstaande interactieve Python sessie wordt afgebeeld is $$(5,0)$$ bijvoorbeeld een dood punt, omdat de twee pompstations die op de vierde avenue gelegen zijn allebei op afstand 4 van het punt $$(5,0)$$ liggen.

>>> manhattanAfstand((3, 5), (7, 9))
8
>>> manhattanAfstand((12, 5), (3, 16))
20
>>> doodpunt((4, 3), [(1, 8), (4, 3), (6, 3), (6, 5)])
False
>>> doodpunt((7, 4), [(1, 8), (4, 3), (6, 3), (6, 5)])
True
>>> manhattan(10, 10, [(1, 8), (4, 3), (6, 3), (6, 5)])
****D*****
****D***P*
*****D****
*****DD***
***P*DDD**
DDDDD***DD
***PDP****
****D*****
****D*****
****D*****