Het bepalen van een opspannende boom is een veelvoorkomend grafenprobleem. Een netwerk van ethernetkabels zal bijvoorbeeld vaak aangelegd worden met redundante kabels. Het spanning tree protocol (STP) zal dynamisch een opspannende boom berekenen en daarmee lussen (cykels) vermijden, verbindingen vervangen wanneer kabels (bogen) het begeven en toch steeds de routes (paden) tussen elke paar nodes voorzien.

Bij het opstellen van een opspannende boom tussen nodes is het voordelig om de vertraging (latency) op het netwerk te minimaliseren. Men zou, als we aan elke verbinding de latency op die verbinding toekennen, dit probleem kunnen herformuleren als het bepalen van een minimale-kost opspannende boom. In de praktijk wordt niet de latency tussen elke twee nodes geminimaliseerd, maar de latency tussen elke node en een root node, waar dan de uplink (de weg naar de rest van het internet) van het lokaal netwerk is.

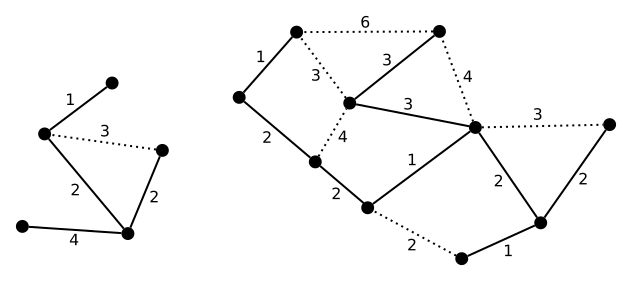
In deze oefening implementeren we het algoritme van Kruskal voor het bepalen van een minimale-kost opspannende boom in een gewogen samenhangende graaf. Gegeven is de interface Spanner¹ en de grafenbibliotheek² (javadoc³) die we reeds kennen van eerdere opgaves. Implementeer deze interface in een klasse Kruskal.

Spanner legt de methode public UndirectedGraph<String> span(UndirectedGraph<String> graph) op, die een deelgraaf van gewogen samenhangende graaf graph zal teruggeven. Hierbij mag je graph niet wijzigen. De deelgraaf die je teruggeeft is een minimale-kost opspannende boom van graph.

Met behulp van SimpleTest⁴ kan je jouw oplossing lokaal testen.