Een strikt positief natuurlijk getal is beleefd als het kan geschreven worden als de som van twee of meer opeenvolgende strikt positieve natuurlijke getallen. Het getal 7 is bijvoorbeeld beleefd omdat het kan geschreven worden als 3 + 4. Beleefde getallen worden soms ook trapgetallen genoemd, omwille van de trapvorm van de Young diagrammen die een grafische voorstelling weergeven van de ontbinding van een beleefd getal in opeenvolgende natuurlijke getallen.
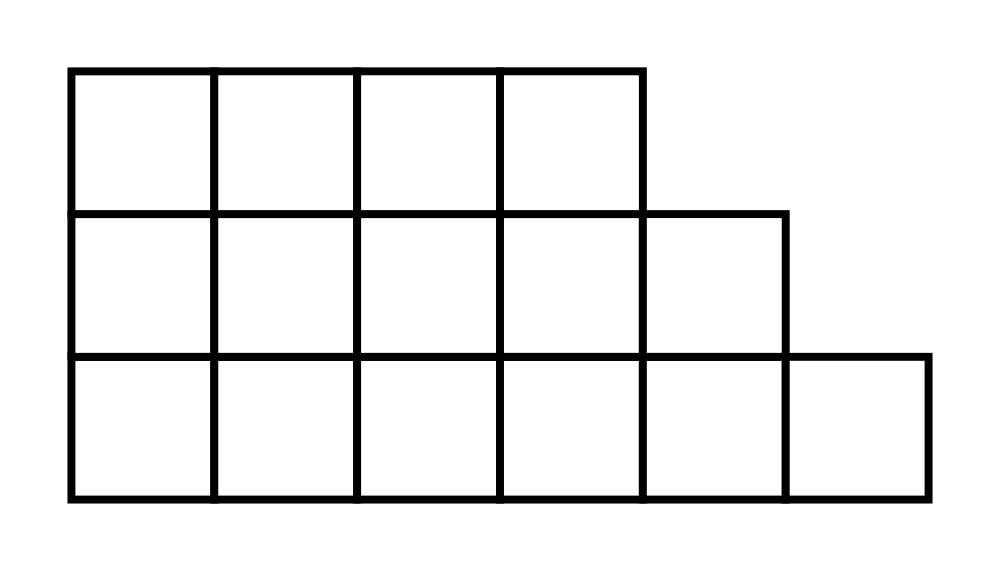
Sommige getallen kunnen op verschillende manieren geschreven worden als de som van twee of meer opeenvolgende getallen. Zo kan 15 bijvoorbeeld op de volgende manieren geschreven worden:
1 + 2 + 3 + 4 + 5 4 + 5 + 6 7 + 8
Het aantal manieren waarop een getal kan geschreven worden als de som van twee of meer opeenvolgende strikt positieve natuurlijke getallen wordt de beleefdheid van het getal genoemd. Elk getal dat een macht van twee is kan niet geschreven worden als de som van twee of meer opeenvolgende getallen. Dergelijke getallen hebben een beleefdheid van 0, en zijn dus onbeleefd.
Invoer
Een getal $$n \in \mathbb{N}_0$$.
Uitvoer
Een getal dat de beleefdheid van het getal $$n$$ aangeeft.
Voorbeeld
Invoer:
15Uitvoer:
3