Stel dat we het oppervlak van de roterende trommel van een wasmachine in zestien gelijke delen verdelen, zoals aangegeven in de linker figuur hieronder. De donkere delen stellen geleidende materialen voor, en de lichte delen niet-geleidende materialen. We stellen de positie van de trommel voor aan de hand van vier binaire cijfers $$a$$, $$b$$, $$c$$ en $$d$$ zoals aangegeven in de rechter figuur hieronder. Afhankelijk van de positie van de trommel zijn de uiteinden die worden voorgesteld door $$a$$, $$b$$, $$c$$ en $$d$$ ofwel geaard of geïsoleerd van de aarde — in onderstaande figuur zijn de geaarde uiteinden bijvoorbeeld $$a$$, $$c$$ en $$d$$. De geaarde eindpunten sturen een signaal uit dat wordt voorgesteld door 1, en de geïsoleerde einpunten stellen een signaal uit dat wordt voorgesteld door 0.

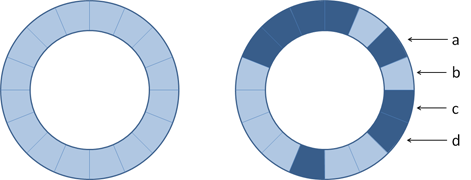
Om ervoor te zorgen dat elk van de zestien posities van de trommels op een unieke manier kan voorgesteld worden door een woord $$abcd$$ van vier binaire cijfers, moeten de geleidende en niet-geleidende materialen op zo'n manier aan de zestien delen toegekend worden dat elk van de zestien mogelijke woorden van vier binaire cijfers $$abcd$$ voorkomen. De vraag die zich stelt is of dit wel mogelijk is. En indien ja, hoe kunnen de materialen dan gerangschikt worden?

De rechter figuur hierboven geeft meteen ook een oplossing voor dit probleem. De positie die getoond wordt correspondeert met het binaire woord 1011. Als we de trommel in tegenwijzerzin roteren dan krijgen we achtereenvolgens de volgende binaire woorden:

0110, 1100, 1001, 0010, 0100, 1000, 0000, 0001, 0011, 0111, 1111, 1110, 1101, 1010, 0101, 1011.

Deze woorden van vier binaire cijfers zijn allemaal verschillend, en stellen elk van de zestien mogelijke posities van de roterende trommel voor.

Het probleem van de roterende trommel en de oplossing op basis van de Bruijn reeksen, vindt toepassingen in de computationele biologie, de productie van pseudo-willekeurige getallen, de cryptografie, de telecommunicatie, en ja, zelfs bij het ontwerpen van wasmachines.

Algoritme

Een de Bruijn reeks van orde $$n$$ is de kortst mogelijke (circulaire) binaire string waarin elk mogelijk woord van $$n$$ bits tenminste één keer voorkomt als deelstring. Zo is de string 0000111101100101 bijvoorbeeld een de Bruijn reeks van orde 4, waarbij elk van de $$2^4$$ mogelijke binaire woorden van lengte 4 (0000, 0001, …, 1111) juist één keer voorkomen. Een mogelijk algoritme om een de Bruijn reeks van orde $$n$$ op te stellen werkt als volgt:

start met een string van $$n$$ opeenvolgende nullen
voeg achteraan een 1 toe als het $$n$$-tuple dat daarmee gevormd wordt nog niet in de string voorkomt; anders voeg je achteraan een 0 toe
herhaal stap 2 totdat de lengte van de string gelijk is aan $$2^n$$

Invoer

Een natuurlijk getal $$n \in \mathbb{N}_0$$.

Uitvoer

De de Bruijn reeks van orde $$n$$ die je bekomt op basis van bovenstaand algoritme.

Voorbeeld

Invoer:

Uitvoer:

0000111101100101