Gegeven zijn een aantal steden die bezocht moeten worden door een handelaar om een bepaald product te verkopen. De handelaar wil daarbij het transport tussen de steden minimaliseren en op het eind van de dag weer aankomen waar hij vertrokken is. Dit probleem is gekend als het handelsreizigersprobleem, ofwel het traveling salesman problem (TSP).

De bedoeling is bijgevolg om een route op te stellen die alle steden precies eenmaal bezoekt en de totale reisafstand minimaliseert. Hierbij mag niet vergeten worden om de trip van de laatste bezochte stad terug naar het beginpunt ook in rekening te brengen.

We gebruiken een gretig benaderingsalgoritme dat gekend staat als 2-opt in de context van TSP. Het basisprincipe van dit algoritme is om een route stap voor stap trachten te verbeteren door lokale wijzigingen aan te brengen van volgende aard:

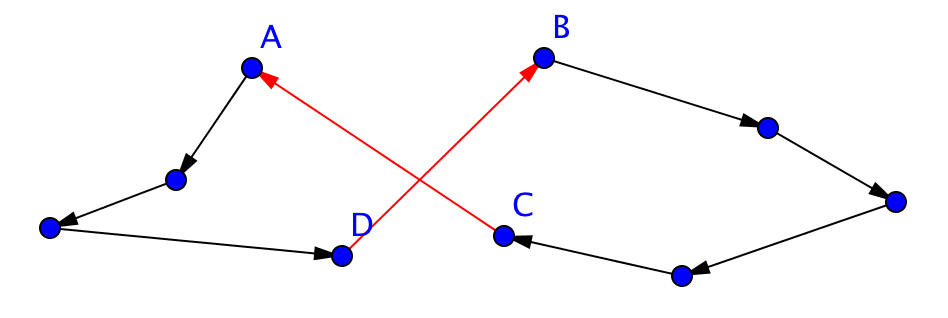
We vervangen in de volgende gegeven route bijvoorbeeld de twee verbindingen C - A en D - B door A - B en C - D:

Dit levert de volgende route op:

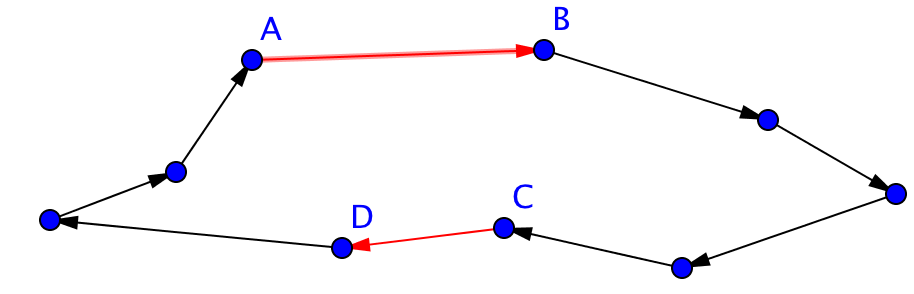
De steden tussen A en D worden dan in omgekeerde volgorde bezocht, wat geen invloed heeft op de totale afstand wegens de symmetrie. Er worden dus slechts 2 afstanden vervangen door 2 andere, vandaar de naam 2-opt. Zo’n wijziging geeft mogelijk een kortere route, bv. wanneer de originele route zichzelf op die plaats kruist (zoals hierboven schematisch weergegeven).

Merk op dat deze wijziging lokaal gezien, voor deze vier steden, de enige mogelijke wijziging is die nog steeds een geldige route oplevert. Indien de verbindingen A - D en B - C zouden gevormd worden, dan krijgen we 2 rondreizen van een kleiner deel van de verzameling steden.

We stellen een route voor als een lijst van steden, in de volgorde waarin ze bezocht worden. Een 2-opt wijziging komt dan overeen met het omkeren van een deelsequentie van deze lijst. Het volledige algoritme gaat als volgt:

1. Start met een gegeven rondreis.
2. Herhaal tot er geen verbetering meer gevonden wordt:
   • Evalueer alle 2-opt wijzigingen tot er één gevonden wordt die de reisafstand verkleint, of tot alle mogelijkheden overlopen zijn.
   • Indien een verbeterende wijziging gevonden werd, pas deze toe.

Opgave

Schrijf een functie TSP2opt(points: list): die een lijst aan (x,y) coordinaten binnenkrijgt, en hierop het TSP2opt algoritme uitvoert. De functie moet de kost van de gevonden rondreis teruggeven, evenals de volgorde waarin de punten bezocht moeten worden.

Voorbeelden

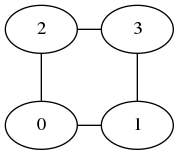
>>> TSP2opt([(0,0),(1,0),(0,1),(1,1)])
(4.0, [0, 1, 3, 2])

->

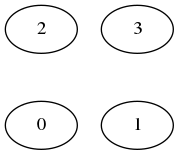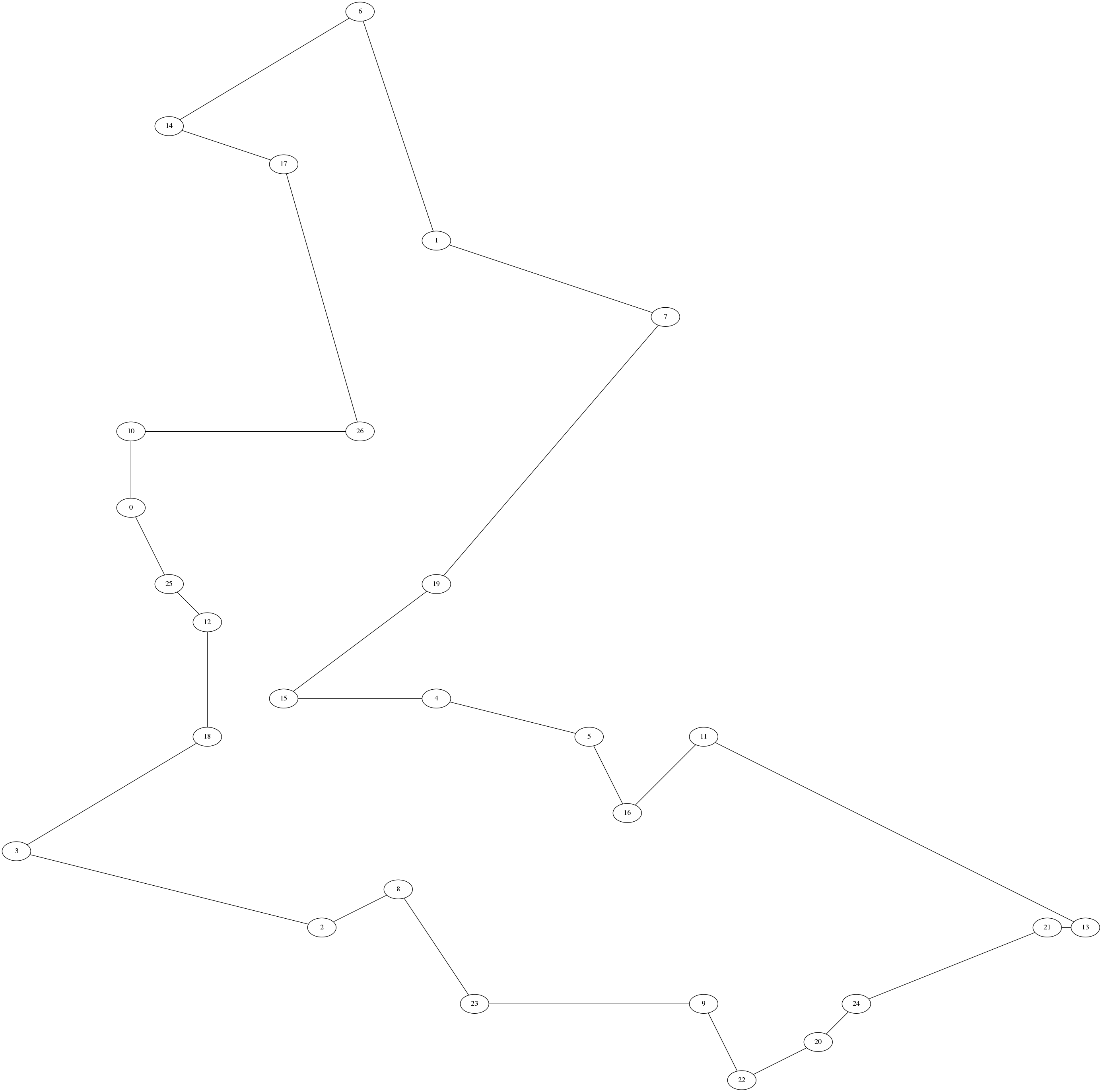
>>> TSP2opt([(3, 15), (11, 22), (8, 4), (0, 6), (11, 10), (15, 9), (9, 28), (17, 20), (10, 5), (18, 2), (3, 17), (18, 9), (5, 12), (28, 4), (4, 25), (7, 10), (16, 7), (7, 24), (5, 9), (11, 13), (21, 1), (27, 4), (19, 0), (12, 2), (22, 2), (4, 13), (9, 17)])
(118.35051342104764, [0, 25, 12, 18, 3, 2, 8, 23, 9, 22, 20, 24, 21, 13, 11, 16, 5, 4, 15, 19, 7, 1, 6, 14, 17, 26, 10])

->

Om je oplossing te visualiseren kun je dit¹ gebruiken.

Extra: Er zijn talloze mogelijkheden om dit algoritme verder uit te werken. Je kan bijvoorbeeld meer complexe wijzigingen overwegen om uit een lokaal optimum te kunnen ontsnappen. Of je kan proberen om de stabiliteit van de oplossing te verhogen door bv. van verschillende routes te starten. Nog een optie is om alle mogelijke 2-opt wijzigingen voor de huidige route te overlopen en hiervan de beste toe te passen, d.w.z. deze die de totale reisafstand het meest verkleint, in plaats van de eerst gevonden verbetering. Voel je vrij om te experimenteren met eigen ideeën.