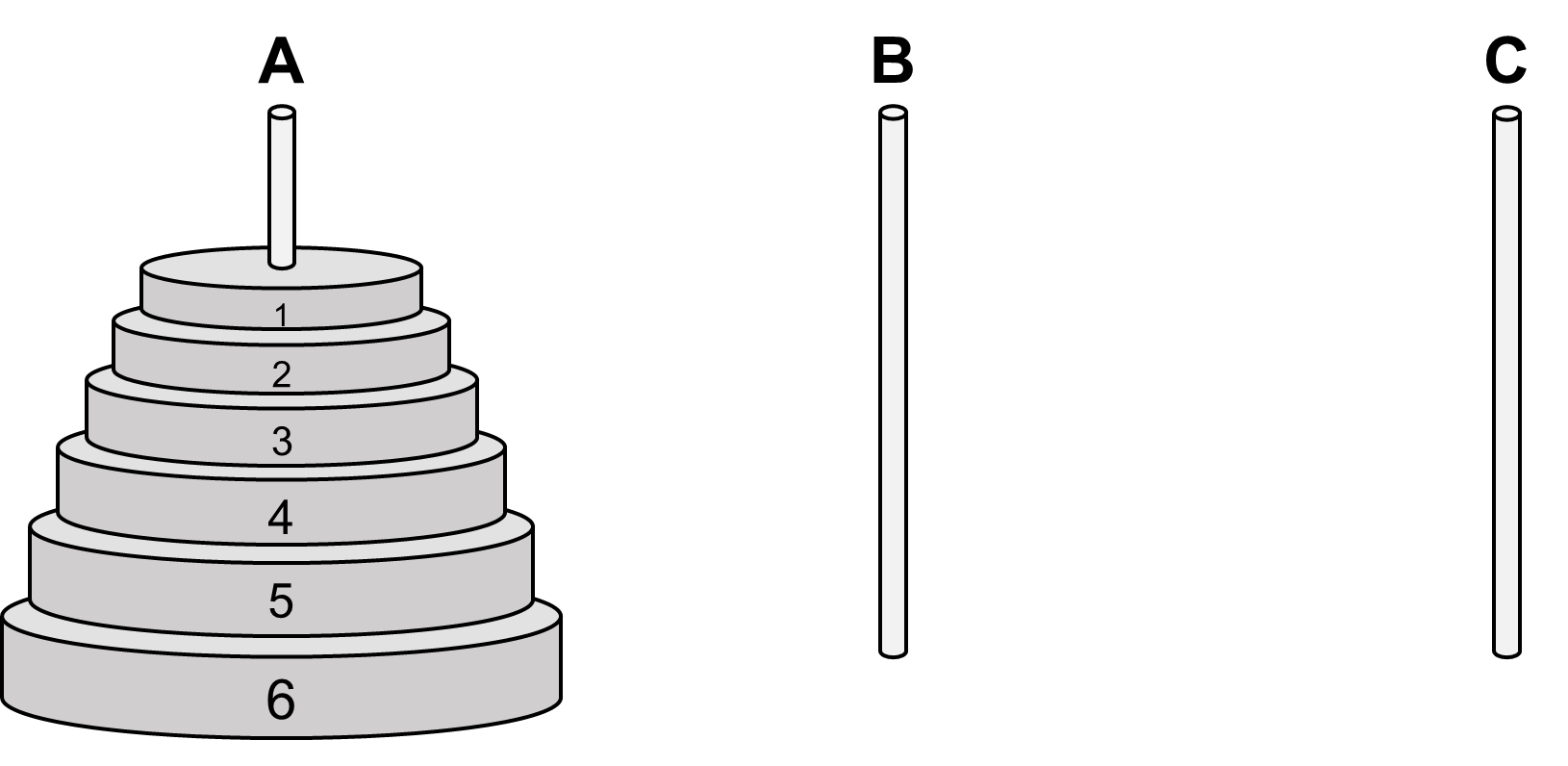
De Torens van Hanoi is een puzzel die gebruik maakt van drie palen, die A, B, en C genoemd worden. Paal A bevat een stapel schijven van verschillende grootte; de schijven zijn genummerd volgens hun grootte. De kleinste schijf is 1, de volgende 2, de volgende 3, etcetera. De grootste schijf is \(n\). Typische waardes voor \(n\) zijn 4 en 5, hoewel in de klassieke puzzel \(n\) de waarde 64 schijnt te hebben. De schijven zijn op paal A gestapeld volgens hun grootte, met de grootste schijf onderaan en de kleinste bovenaan. Je moet nu alle schijven verplaatsen van paal A naar paal C, waarbij je vier regels in acht moet nemen:
-
je mag mag maar één schijf per keer verplaatsen;
-
je mag alleen maar schijven verplaatsen tussen de palen;
-
je mag alleen een schijf verplaatsen die bovenop een stapel ligt, en je kunt hem alleen verplaatsen naar de top van een andere stapel;
-
je mag nooit een schijf plaatsen op een schijf die kleiner is.
Opgave
Schrijf een functie hanoi die deze puzzel oplost voor een willekeurige waarde
van \(n\). De funtie met de oplossing printen als een recept, met regels als
Schijf 1 van A naar C.
Druk aan het einde van het recept het aantal benodigde stappen af.
Tip
Voor een recursieve oplossing, bedenk het volgende: Stel dat je de puzzel moet oplossen waarbij de grootste schijf 10 is. Dit is niet moeilijk als je hem op kunt lossen voor grootte 9. Je gebruikt dan de procedure voor grootte 9 om de bovenste 9 schijven te verplaatsen van paal A naar paal B, je verplaatst vervolgens schijf 10 van paal A naar paal C, en tenslotte gebruik je de procedure voor grootte 9 om de overgebleven 9 schijven te verplaatsen van paal B naar paal C. Maar hoe los je de puzzel op met de grootste schijf 9? Dat is niet moeilijk als je hem kunt oplossen voor grootte 8… Je kunt je voorstellen waar dit heengaat. Je kunt de complexiteit van het probleem stap-voor-stap reduceren, totdat je stelt “het is gemakkelijk om het probleem op te lossen voor grootte 2 als je het kunt oplossen voor grootte 1.” Oplossen voor grootte 1 is triviaal: je verplaatst gewoon de schijf naar de paal waar hij heen moet. Dit is een recursieve definitie van de oplossing:
Om de puzzle op te lossen voor grootte \(n\) waarbij je de stapel moet verplaatsen van paal X naar paal Y met paal Z als tijdelijke paal, dan los je het eerst op voor grootte \(n-1\) waarbij je de stapel verplaatst van paal X naar paal Z met paal Y als tijdelijke paal, dan verplaats je de schijf met grootte \(n\) van paal X naar paal Y, en tenslotte los je het probleem op voor grootte \(n-1\) waarbij je van paal Z naar paal Y gaat met paal X als tijdelijke paal.
Voorbeeld
>>> hanoi(4)
Schijf 1 van A naar B
Schijf 2 van A naar C
Schijf 1 van B naar C
Schijf 3 van A naar B
Schijf 1 van C naar A
Schijf 2 van C naar B
Schijf 1 van A naar B
Schijf 4 van A naar C
Schijf 1 van B naar C
Schijf 2 van B naar A
Schijf 1 van C naar A
Schijf 3 van B naar C
Schijf 1 van A naar B
Schijf 2 van A naar C
Schijf 1 van B naar C
15 stappen gedaan