Begin jaren 1970 bestudeerde antropoloog Wayne Zachary van Temple University1 (Philadelphia, Pennsylvania, VSA) een plaatselijke karateclub waarin onenigheid was ontstaan tussen de leraar en de voorzitter. Die ruzie verdeelde de 34 leden van de club uiteindelijk in twee kampen. Door de communicatiestroom tussen de leden van de club te onderzoeken, slaagde Zachary erin om op één uitzondering na te voorspellen welke kant elk lid van de club zou kiezen in het geschil: die van de leraar of die van de voorzitter.
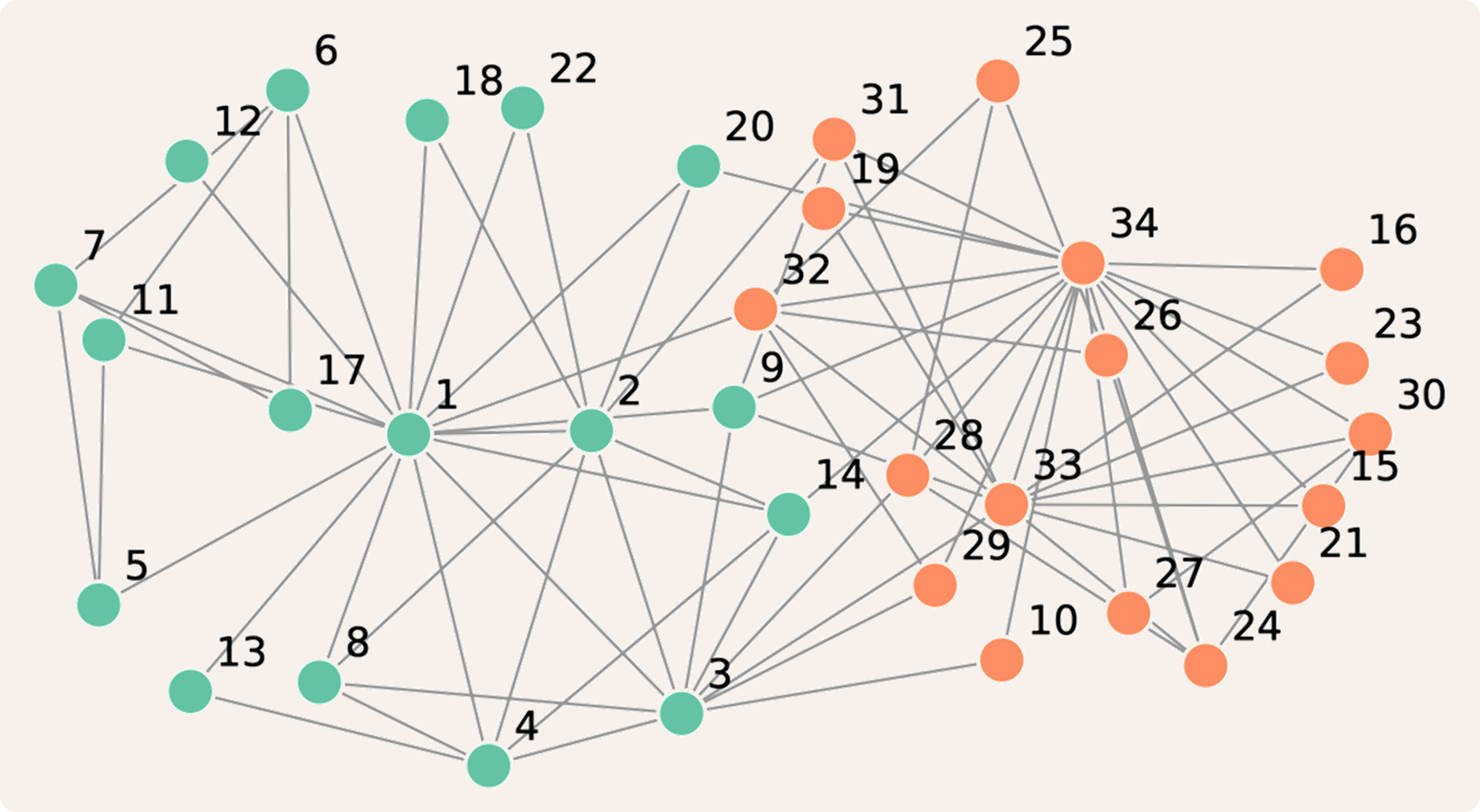
Deze anekdote is een populair voorbeeld geworden in het onderzoek naar gemeenschapsstructuur in netwerken. In die mate zelfs dat wetenschappers nu een prijs uitreiken aan de eerste persoon die dit voorbeeld aanhaalt op een conferentie. Het originele voorbeeld staat bekend als Zachary's Karate Club. De winnaars van de prijs vormen Zachary's Karate Club Club2.
Opgave
In een netwerk $$\mathcal{N}$$ met $$n$$ knopen worden de knopen genummerd van 1 tot en met $$n$$. De capaciteit $$c_{i,j}$$ is een maat voor de sterkte van de communicatiestroom tussen knoop $$i$$ en knoop $$j$$ in netwerk $$\mathcal{N}$$: hoe hoger de capaciteit, hoe sterker de communicatiestroom tussen de twee knopen. We beschouwen enkel netwerken waarvoor de capaciteiten voldoen aan:
-
$$c_{i,j} \in \mathbb{N}$$, met $$0 \leq c_{i,j} < 10$$ voor alle $$1 \leq i, j \leq n$$
-
$$c_{i,j} = c_{j,i}$$ voor alle $$1 \leq i, j \leq n$$
-
$$c_{i,i} = 0$$ voor alle $$1 \leq i \leq n$$
Een capaciteitsbestand voor een netwerk $$\mathcal{N}$$ is een tekstbestand dat alle capaciteiten van het netwerk beschrijft. Het bestand bevat $$n$$ regels die elk uit $$n$$ cijfers (0–9) bestaan. Als we de regels van boven naar onder nummeren vanaf 1, en ook de posities van de cijfers op elke regel van links naar rechts nummeren vanaf 1, dan staat het $$j$$-de cijfer op regel $$i$$ voor de capaciteit $$c_{i,j}$$ van netwerk $$\mathcal{N}$$. Dit is bijvoorbeeld het capaciteitsbestand voor de 34 leden van Zachary's Karate Club (karate.txt3):
0453333220232300020202000000000200 4063000400000500010202000000002000 5603000451000300000000000002200030 3330000300003300000000000000000000 3000002000300000000000000000000000 3000005000300000300000000000000000 3000250000000000300000000000000000 2443000000000000000000000000000000 2050000000000000000000000000003043 0010000000000000000000000000000002 2000330000000000000000000000000000 3000000000000000000000000000000000 2003000000000000000000000000000000 3533000000000000000000000000000003 0000000000000000000000000000000032 0000000000000000000000000000000034 0000033000000000000000000000000000 2100000000000000000000000000000000 0000000000000000000000000000000012 2200000000000000000000000000000001 0000000000000000000000000000000031 2200000000000000000000000000000000 0000000000000000000000000000000020 0000000000000000000000000504020054 0000000000000000000000000203000200 0000000000000000000000052000000700 0000000000000000000000000000040002 0020000000000000000000043000000004 0020000000000000000000000000000202 0000000000000000000000020040000042 0200000030000000000000000000000033 2000000000000000000000002700200044 0030000040000033001030250000043405 0000000032000324002110340024223450
Een groep met knopen van een netwerk $$\mathcal{N}$$ met $$n$$ knopen wordt voorgesteld als een collectie (list, tuple of set) met de volgnummers (int) van de knopen. Die collectie mag dus enkel bestaan uit gehele getallen tussen 1 en $$n$$. Bovendien mag elk volgnummer hoogstens één keer in de collectie voorkomen. De volgorde van de volgnummers in de collectie speelt geen rol.
Gevraagd wordt:
-
Schrijf een functie lees_netwerk waaraan de locatie (str) van een capaciteitsbestand voor een netwerk $$\mathcal{N}$$ moet doorgegeven worden. De functie moet een dictionary (dict) teruggeven, die elke knoop $$i$$ (int) in netwerk $$\mathcal{N}$$ afbeeldt op een dictionary (dict) die elke knoop $$j$$ (int) waarvoor $$c_{i,j} > 0$$ in netwerk $$\mathcal{N}$$ afbeeldt op de capaciteit $$c_{i,j}$$ (int) van netwerk $$\mathcal{N}$$. Het resultaat dat door deze functie wordt teruggegeven, noemen we de capaciteitsdictionary van netwerk $$\mathcal{N}$$.
-
Schrijf een functie complementaire_groep waaraan twee argumenten moeten doorgegeven worden: i) een groep $$g$$ (list, tuple of set) met knopen (int) van een netwerk $$\mathcal{N}$$ en ii) de capaciteitsdictionary (dict) van netwerk $$\mathcal{N}$$. Als het eerste argument geen geldige groep voorstelt, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige groep. Anders moet de functie de complementaire groep $$\bar{g}$$ teruggeven: een verzameling (set) met alle knopen (int) van netwerk $$\mathcal{N}$$ die niet tot groep $$g$$ behoren.
-
Schrijf een functie stroom waaraan twee argumenten moeten doorgegeven worden: i) een groep $$g$$ (list, tuple of set) met knopen (int) van een netwerk $$\mathcal{N}$$ en ii) de capaciteitsdictionary (dict) van netwerk $$\mathcal{N}$$. Als het eerste argument geen geldige groep voorstelt, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige groep. Anders moet de functie de sterkte van de communicatiestroom (int) tussen groep $$g$$ en diens complementaire groep $$\bar{g}$$ teruggeven: de som van alle capaciteiten $$c_{i,j}$$ voor alle $$i \in g$$ en alle $$j \in \bar{g}$$.
Voorbeeld
In onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand karate.txt4 zich in de huidige directory bevindt.
>>> netwerk = lees_netwerk('karate.txt5')
>>> netwerk[11]
{1: 2, 5: 3, 6: 3}
>>> netwerk[24]
{26: 5, 28: 4, 30: 2, 33: 5, 34: 4}
>>> groep = [1, 2, 3, 4, 5, 6, 7, 8, 11, 12, 13, 14, 17, 18, 20, 22]
>>> complementaire_groep(groep, netwerk) # doctest: +SKIP
{9, 10, 15, 16, 19, 21, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34}
>>> complementaire_groep((1, 2, 3, 2), netwerk)
Traceback (most recent call last):
AssertionError: ongeldige groep
>>> stroom(groep, netwerk)
23
>>> stroom(set(groep) | {9}, netwerk)
26
>>> stroom((1, 2, 3, 2), netwerk)
Traceback (most recent call last):
AssertionError: ongeldige groep
Epiloog
De persoon die door Zachary aan het verkeerde kamp werd toegewezen, komt overeen met knoop 9 in het netwerk uit de inleiding van deze opgave. Bij de splitsing van de karateclub sloot die persoon zich aan bij de nieuwe club met supporters van de leraar (knoop 1), ondanks het feit dat hij een zwakke supporter van de voorzitter (knoop 34) was. Deze keuze kwam vooral voort uit opportunisme: op het moment van de splitsing waren er nog drie weken te gaan voor hij examen voor de zwarte band (hoogste rang) kon afleggen. Had hij voor de nieuwe club van de voorzitter gekozen, dan moest hij zijn rang opgeven en opnieuw beginnen in een nieuwe karatestijl met een witte (beginners)band. De voorzitter had immers beslist om van karatestijl te veranderen voor zijn nieuwe club. Na vier jaar geoefend te hebben in de stijl van de leraar, kon het lid het niet opbrengen om zijn rang op te geven en helemaal opnieuw te beginnen.