Long repeats

We saw in "Introduction to pattern matching¹" that a data structure commonly used to encode the relationships among a collection of strings was the trie, which is particularly useful when the strings represent a collection of patterns that we wish to match to a larger text.

The trie is helpful when processing multiple strings at once, but when we want to analyze a single string, we need something different.

In this assignment, we will use a new data structure to handle the problem of finding long repeats in the genome. Recall from "Finding a motif in DNA²" that cataloguing these repeats is a problem of the utmost interest to molecular biologists, as a natural correlation exists between the frequency of a repeat and its influence on RNA transcription. Our aim is therefore to identify long repeats that occur more than some predetermined number of times.

Assignment

A repeated substring of a string $$s$$ of length $$n$$ is simply a substring that appears in more than one location of $$s$$. More specifically, a $$k$$-fold substring appears in at least $$k$$ distinct locations.

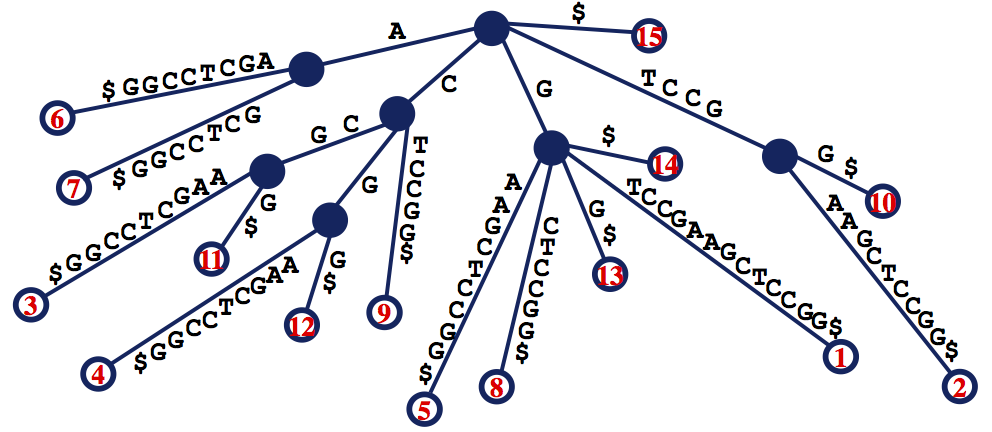
The suffix tree of $$s$$, denoted $$T(s)$$, is defined as follows:

$$T(s)$$ is a rooted tree having exactly $$n$$ leaves
every edge of $$T(s)$$ is labeled with a substring of $$s^∗$$, where $$s^∗$$ is the string formed by adding a placeholder symbol $ to the end of $$s$$.
every internal node of $$T(s)$$ other than the root has at least two children; i.e., it has degree at least 3
the substring labels for the edges leading from a node to its children must begin with different symbols
by concatenating the substrings along edges, each path from the root to a leaf corresponds to a unique suffix of $$s^∗$$.

The figure below shows an example of a suffix tree.

The suffix tree for $$s$$ = GTCCGAAGCTCCGG. Note that the dollar sign has been appended to a substring of the tree to mark the end of $$s$$. Every path from the root to a leaf corresponds to a unique suffix of GTCCGAAGCTCCGG, and each leaf is labeled with the location in $$s$$ of the suffix ending at that leaf.

Write a function longestRepeatedSubstring that takes two arguments: i) a DNA string $$s$$ and ii) an integer $$k \in \mathbb{N}_0$$. The function must return the longest substring of $$s$$ that occurs at least $$k$$ times in $$s$$. If multiple solutions exist, the function may return any solution. If no solutions exist, the function must return the value None.

Example

In the following interactive session, we assume the FASTA file data.fna³ to be located in the current directory.

        >>> longestRepeatedSubstring('CATACATAC', 2)
'CATAC'
>>> from Bio import SeqIO
>>> longestRepeatedSubstring(*SeqIO.parse('data.fna', 'fasta'), 19)
'AAAAC'