Trilateratie is het bepalen van de (relatieve) positie van een punt aan de hand van de afstanden van dit punt tot enkele gekende punten. Hierbij wordt gesteund op de meetkundige eigenschappen van cirkels. In tegenstelling tot triangulatie worden er bij trilateratie geen hoeken gemeten. Deze techniek heeft enkele zeer praktische toepassingen zoals het GPS-systeem, het bepalen van het epicentrum van een aardbeving, …
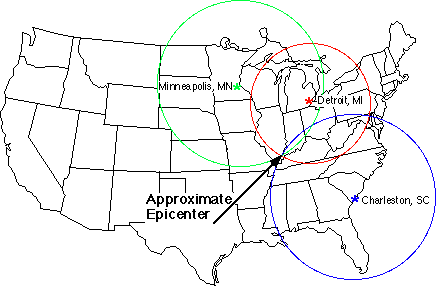
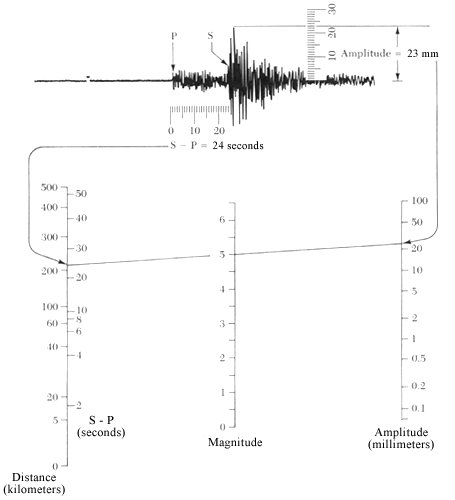
Om bijvoorbeeld het epicentrum van een aardbeving te bepalen, kan je als volgt te werk gaan. Je bepaalt voor verschillende meetstation de tijd tussen de eerste P-golf en de eerste S-golf. Aan de hand van gekende tabellen kan je hieruit de afstand van het epicentrum tot het meetstation bepalen. Zo zie je op onderstaande afbeelding dat een verschil van 24 seconden tussen de eerste P-golf en de eerste S-golf correspondeert met een epicentrum op een afstand van 215 km. Dit geeft je dus een cirkel waarop het epicentrum kan liggen. Als je meerdere meetpunten hebt, dan wordt het epicentrum gegeven door het snijpunt van de verschillende cirkels. In werkelijkheid zal hier steeds een meetfout op zitten en zal je nooit echt een mooi snijpunt vinden, maar eerder een gebied van mogelijkheden.
Opgave
Een belangrijk onderdeel van trilateratie is het bepalen van de onderlinge positie van twee cirkels. Hieronder zie je een overzicht van de mogelijke onderlinge posities van twee cirkels. In deze tabel staat $$d$$ voor de afstand tussen de middelpunten van de twee cirkels en $$r_1$$ (respectievelijk $$r_2$$) voor de straal van de eerste (respectievelijk de tweede) cirkel.
| positie | voorwaarde |
|---|---|
| concentrisch | $$d = 0$$ |
| binnen rakend | $$d = |r_1 - r_2|$$ |
| buiten rakend | $$d = r_1 + r_2$$ |
| omsluitend | $$d < |r_1 - r_2|$$ |
| snijdend | $$|r_1 - r_2| < d < r_1 + r_2$$ |
| gescheiden | $$d > r_1 + r_2$$ |
De afstand $$d$$ tussen twee punten $$(x_1,y_1)$$ en $$(x_2,y_2)$$ wordt hierbij berekend aan de hand van de volgende formule:
$$d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$$
Waarschuwing
Als je met reële getallen werkt op een computer, dan treden er al snel afrondingsfouten op. Hierdoor zullen twee getallen die gelijk zouden moeten zijn, vaak net niet gelijk zijn. Daarom gebruiken we een foutmarge bij het vergelijken van twee reële getallen: we zeggen dan bijvoorbeeld dat twee reële getallen gelijk zijn, als het verschil tussen deze twee getallen kleiner is dan $$10^{-6}$$.
Invoer
Zes reële getallen: één getal per regel. De eerste drie getallen zijn respectievelijk de $$x$$-coördinaat, de $$y$$-coördinaat en de straal van een eerste cirkel. De laatste drie getallen zijn respectievelijk de $$x$$-coördinaat, de $$y$$-coördinaat en de straal van een tweede cirkel.
Uitvoer
Een regel die één van de volgende termen bevat:
-
concentrisch
-
binnen rakend
-
buiten rakend
-
omsluitend
-
snijdend
-
gescheiden
De term die moet uitgeschreven worden, moet de onderlinge positie van de twee gegeven cirkels aanduiden.
Voorbeeld
Invoer:
3.5
2.7
7.86
6.5
6.7
2.86Uitvoer:
binnen rakendOp onderstaande grafische voorstelling van de twee gegeven cirkels zie je duidelijk dat ze elkaar van binnen raken. De eerste cirkel wordt in het oranje weergegeven, en de tweede cirkel in het paars.