In 1984 was het publiek dat een opname van het televisieprogramma Press Your Luck aan het bijwonen was met verstomming geslagen, nadat deelnemer Michael Larson zomaar eventjes $110.237 had gewonnen. Dat was tot op dat moment veruit het hoogste prijzengeld ooit op één dag gewonnen bij een spelshow. Terwijl de lichten willekeurig flikkerden over Big Board — de naam die in de show aan het spelbord gegeven werd — slaagde Larson er op de één of andere manier steeds in om te stoppen bij een scherm dat een geldprijs én extra beurten opleverde, en de "whammy" te vermijden die hem bankroet zou maken.

Paul Michael Larson

Achteraf zou blijken dat het patroon waarmee de lichten over het spelbord flikkerden toch niet zo willekeurig was. Thuis had Larson het spel minutieus bestudeerd, en daarbij had hij ontdekt dat het verloop van de lichten gebaseerd was op vijf herkenbare patronen. Nadat hij deze patronen van buiten geleerd had, kon hij garanderen dat hij altijd op een winnend scherm terechtkwam.

De producenten van CBS vervloekten de regelmaat in het gedrag van het spelbord, maar ze konden geen enkele reden aanbrengen om Larson te diskwalificeren omdat hij geen enkele spelregel met de voeten getreden had. Ze betaalden hem zijn prijzengeld uit, pasten het spelbord aan, en legden een maximumbedrag op die toekomstige deelnemers konden winnen. Larsen mag zichzelf wel op de borst geslagen hebben, toch kreeg hij niet veel tijd om van zijn winst te genieten — hij verloor het geld in slechte vastgoedinvesteringen en stierf aan keelkanker op de leeftijd van 49 jaar.

Opgave

Hieronder staat een voorbeeld van de configuratie van Big Board, het spelbord dat gebruikt werd in het televisieprogramma Press Your Luck. Het spelbord bestond uit $$p$$ vierkanten (in het voorbeeld is $$p=18$$) die in een rechthoek gerangschikt zijn, en in elk vierkant werd steeds één van $$s$$ schermen getoond (in het voorbeeld is $$s=3$$). Als een speler aan de beurt kwam, begon er een snelle cyclus waarin bij elke stap in elk vierkant één van de $$s$$ schermen getoond werd en één willekeurig vierkant fel oplichtte. De speler kon de cyclus stoppen door op zijn drukknop aan te slaan, waarna hij de prijs won die op het opgelichte scherm verscheen of al zijn verzamelde geld verloor als hij op een whammy terechtkwam.

Configuratie van Big Board, het spelbord dat gebruikt werd in het televisieprogramma Press Your Luck. Het spelbord bestaat uit 18 vierkanten, waarbij in elk vierkant telkens één van drie schermen getoond wordt. De "+S" geeft aan dat de deelnemer een extra beurt (spin) krijgt, een eigenschap van het spel die centraal stond in de strategie van Larson om te blijven verderspelen.

Larson had echter een zekere regelmaat ontdekt in het schijnbaar willekeurig gedrag van het spelbord. Elke cyclus werd immers bepaald door een patroon dat bestond uit een aantal natuurlijke getallen en een vierkant dat wordt opgelicht bij aanvang van de cyclus. Bij elke stap in de cyclus wordt het spelbord op twee manieren gewijzigd, die onafhankelijk van elkaar werken:

Het volgende vierkant dat wordt opgelicht, wordt bepaald door het volgende getal te nemen uit het patroon (te beginnen bij het eerste getal, en na het laatste getal volgt terug het eerste getal), en zoveel vierkanten in wijzerinzin vooruit te springen op het spelbord. Door de rechthoekige vorm van het spelbord, volgt na het laatste vierkant terug het eerste vierkant.
Bij aanvang van een cyclus wordt in elk vierkant het eerste scherm getoond. Bij elke stap van de cyclus wordt in elk vierkant het volgende scherm uit de reeks van $$s$$ schermen getoond, waarbij na het laatste scherm terug het eerste scherm getoond wordt.

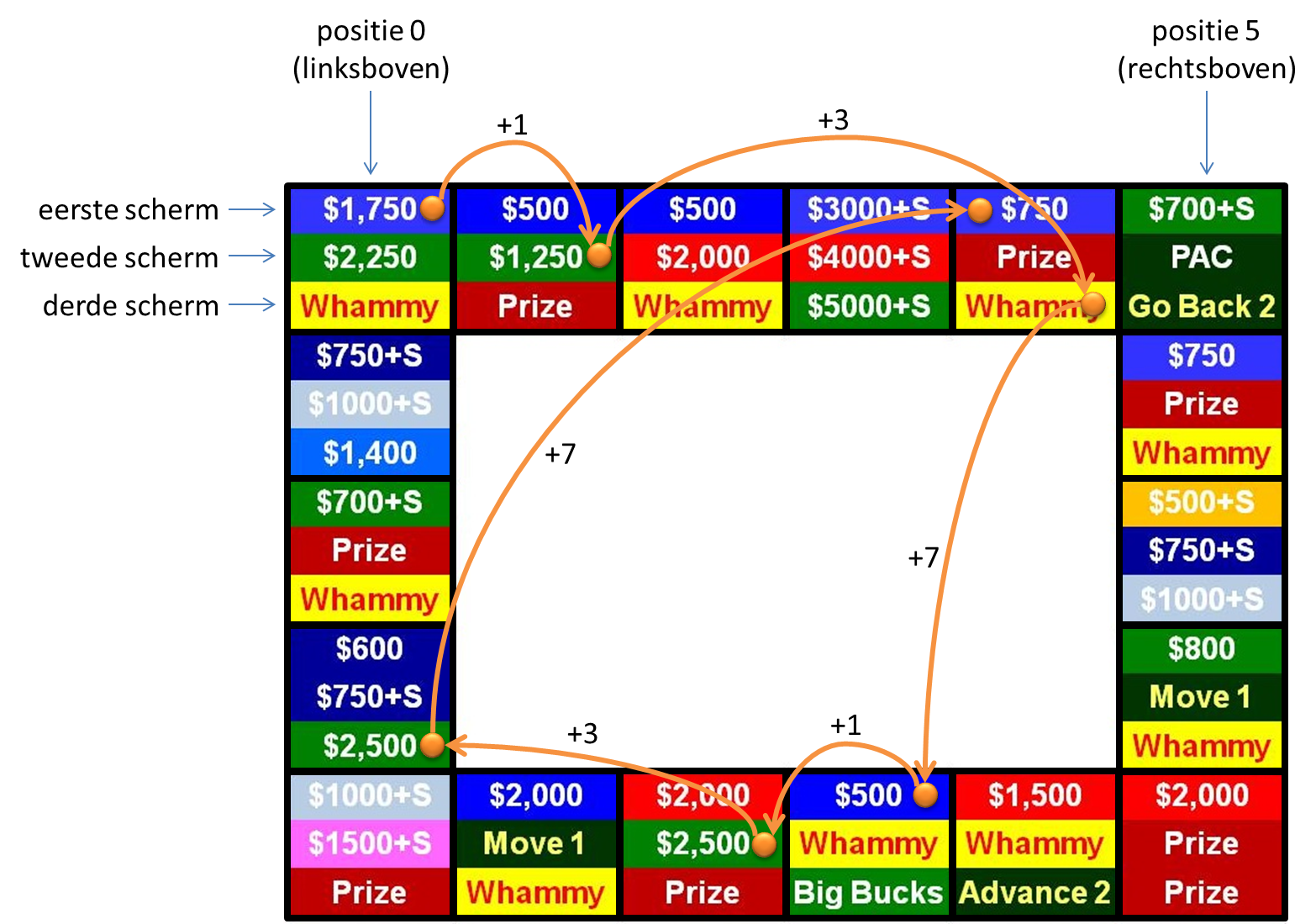
De procedure wordt in bovenstaande figuur uitgelegd aan de hand van een cyclus met patroon [1, 3, 7] die begint bij het vierkant in de linkerbovenhoek. Bij aanvang van de cyclus wordt in de linkerbovenhoek het scherm met $1750 getoond, op het vierkant rechts daarvan het scherm met $500, enzoverder. In een eerste stap springt het licht 1 vierkant vooruit in wijzerzin, en wordt in elk vierkant het tweede scherm getoond. Als we nu zouden afdrukken, dan wordt het scherm met $1250 opgelicht. In een volgende stap springt het licht 3 vierkanten vooruit in wijzerin, en wordt het derde scherm met whammy opgelicht. In een volgende stap springt het licht 7 vierkanten vooruit, en wordt terug het eerste scherm met $500 opgelicht (in de vorige stap werd in elk vierkant steeds het laatste van de drie schermen opgelicht). In een volgende stap springt het licht terug 1 vierkant vooruit (na het laatste getal in het patroon gebruiken we terug het eerste getal), en wordt het tweede scherm met $2500 opgelicht. De figuur toont ook nog de twee volgende stappen uit de cyclus. Gevraagd wordt:

Schrijf een functie spelbord waaraan een reeks (een lijst of een tuple) van strings moet doorgegeven worden. Deze reeks van strings stelt de prijzen (of whammies) voor waarmee een Big Board geconfigureerd wordt met $$s \in \mathbb{N}_0$$ schermen per vierkant. De waarde $$s$$ kan aan de functie doorgegeven worden via een tweede optionele parameter schermen (standaardwaarde: 1). De functie moet een lijst van vierkanten teruggeven, waarbij elk vierkant zelf ook een lijst is die gevuld wordt met de volgende $$s$$ strings uit de gegeven reeks van strings. Elk vierkant stelt op die manier de reeks schermen met prijzen voor die achtereenvolgens in het vierkant getoond worden.
Gebruik de functie spelbord om een functie prijs te schrijven. De functie moet de prijs (string) teruggeven die oplicht op het spelbord nadat een aantal stappen werden uitgevoerd volgens een bepaalde cyclus van het spelbord. Het spelbord, het aantal stappen en de cyclus worden bepaald door de waarden die doorgegeven worden aan de verplichte en optionele parameters van de functie:

patroon (verplicht): reeks (lijst of tuple) van getallen $$\in \mathbb{N}_0$$ die het patroon beschrijft
stappen (verplicht): getal $$\in \mathbb{N}_0$$ dat het aantal stappen aangeeft
prijzen (verplicht): reeks (lijst of tuple) van strings die de configuratie van het spelbord beschrijft (zie functie spelbord)
start (optioneel; standaardwaarde: 0): getal $$\in \mathbb{N}_0$$ dat de positie aangeeft van het vierkant waar de cyclus start; vierkanten worden hierbij in wijzerzin genummerd, startend vanaf het vierkant in de linkerbovenhoek dat op positie 0 staat
schermen (optioneel; standaardwaarde: 1): getal $$\in \mathbb{N}_0$$ dat het aantal schermen per vierkant aangeeft (zie functie spelbord)

Beide functies moeten een AssertionError opwerpen met de boodschap ongeldig spelbord, indien het aantal prijzen in de gegeven reeks van strings geen veelvoud is van $$s$$.

Voorbeeld

>>> prijzen = ('$100', '$200', '$300', '$400', '$500', '$600', '$700', '$800', '$900', '$1000', 'whammy', '$1100', '$1200', '$1300', '$1400', '$1500')

>>> spelbord(prijzen)
[['$100'], ['$200'], ['$300'], ['$400'], ['$500'], ['$600'], ['$700'], ['$800'], ['$900'], ['$1000'], ['whammy'], ['$1100'], ['$1200'], ['$1300'], ['$1400'], ['$1500']]
>>> spelbord(prijzen, schermen=2)
[['$100', '$200'], ['$300', '$400'], ['$500', '$600'], ['$700', '$800'], ['$900', '$1000'], ['whammy', '$1100'], ['$1200', '$1300'], ['$1400', '$1500']]
>>> spelbord(prijzen, schermen=4)
[['$100', '$200', '$300', '$400'], ['$500', '$600', '$700', '$800'], ['$900', '$1000', 'whammy', '$1100'], ['$1200', '$1300', '$1400', '$1500']]
>>> spelbord(prijzen, schermen=3)
Traceback (most recent call last):
AssertionError: ongeldig spelbord

>>> prijs(patroon=[1, 3, 7], stappen=1, prijzen=prijzen, schermen=2)
'$400'
>>> prijs(patroon=[1, 3, 7], stappen=2, prijzen=prijzen, schermen=2, start=1)
'whammy'
>>> prijs(patroon=[5, 2, 9, 3], stappen=20, prijzen=prijzen, schermen=4, start=4)
'$1200'