Polka Dot is een puzzel waarvoor je elf kaarten nodig hebt die genummerd zijn van 0 tot en met 10. Alle kaarten hebben dezelfde achterkant, waardoor ze niet van elkaar kunnen onderscheiden worden. Rangschik de kaarten met hun achterkant naar boven op een stapel. Deel vervolgens de bovenste kaart door hem omgedraaid op tafel te leggen (zodat je het nummer op de kaart kan lezen), verplaats de volgende kaart naar de onderkant van de stapel, deel de volgende kaart, verplaatst de volgende kaart naar de onderkant van de stapel, enzoverder. Blijf dit proces herhalen totdat je alle kaarten gedeeld hebt.
Kan je de kaarten in de oorspronkelijke stapel zo rangschikken dat ze in oplopende volgorde gedeeld worden: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10? Onderstaande video toont alvast hoe de kaarten in de juiste volgorde moeten gedeeld worden.
Dit is een klassieke puzzel die gebruikt wordt om kinderen op een probleemoplossende manier te leren denken. Als initieel blijkt dat elf kaarten te moeilijk zijn, dan kunnen ze eerst beginnen met drie, vijf of zeven kaarten om zo de uitdaging steeds groter te maken, totdat er zich een vast oplossingspatroon begint af te tekenen.
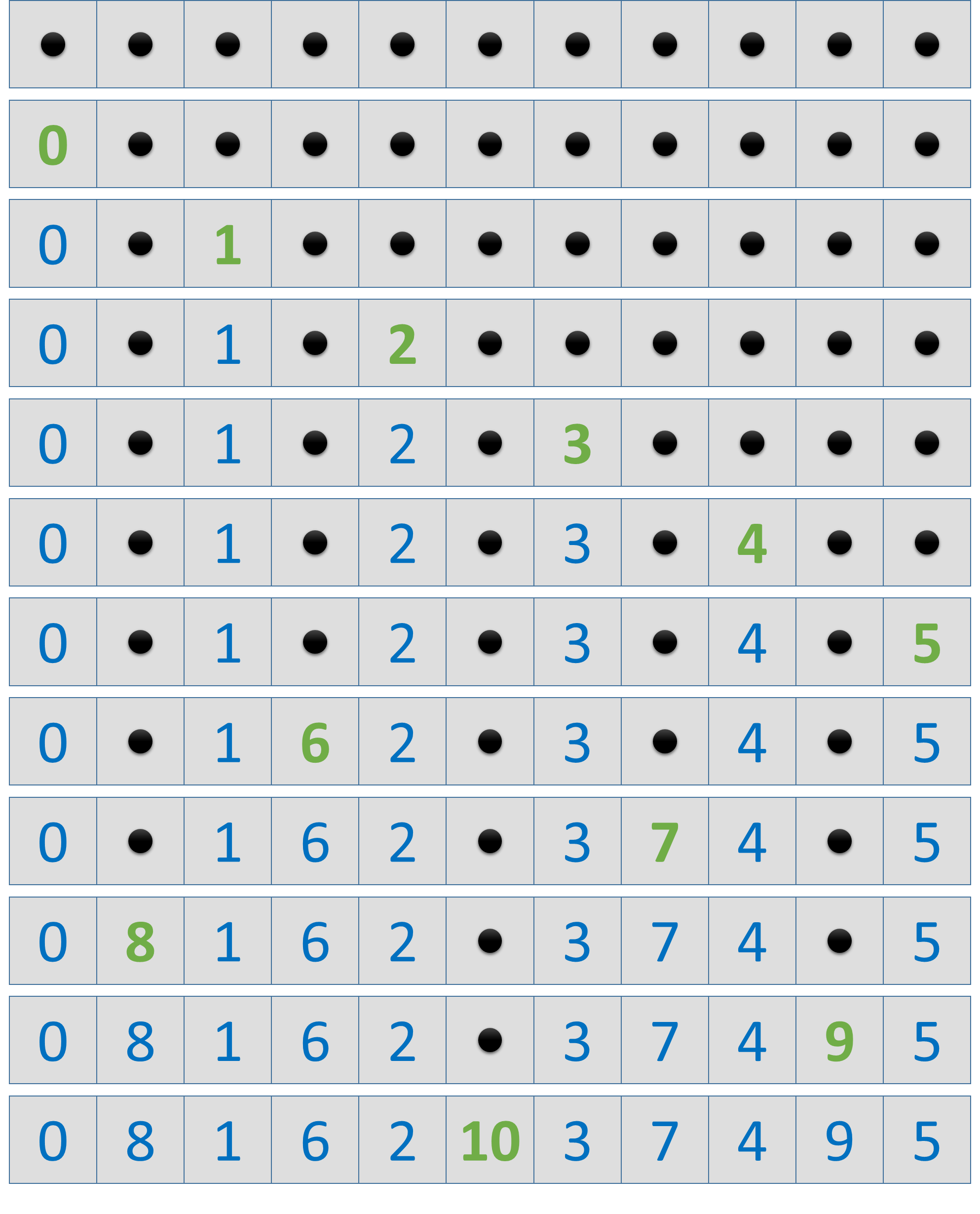
Er bestaan heel wat verschillende manieren om dit probleem aan te pakken, maar dit is wellicht de meeste elegante oplossingsmethode. Zet evenveel stippen naast elkaar als er kaarten zijn. Plaats een nul op de eerste stip. Vertrekkend vanaf de stip waarop je laatst een getal geplaatst hebt, plaats je telkens het volgende getal op de tweede stip waarop nog geen getal geplaatst werd — als je het einde van de reeks stippen bereikt, ga dan verder aan het begin van de reeks. Herhaal deze procedure totdat er op alle stippen getallen geplaatst zijn. Onderstaand schema illustreert deze procedure voor elf kaarten die in de volgorde 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 moeten gedeeld worden.
Opgave
Bovenstaande procedure werkt niet enkel voor getallen, maar voor elke reeks items, ongeacht de lengte van de reeks. Gevraagd wordt:
-
Schrijf een functie delen waaraan een reeks (list, tuple of str) items moet doorgegeven worden. De functie moet een nieuwe lijst (list) teruggeven die aangeeft in welk volgorde de items uit de gegeven reeks gedeeld worden, als je de manier van delen van de Polka Dot puzzel gebruikt.
-
Schrijf een functie polka waaraan een reeks (list, tuple of str) items moet doorgegeven worden. De gegeven reeks geeft de volgorde aan waarin we de items willen delen op de manier zoals ze gebruikt wordt bij de Polka Dot puzzel. De functie moet een nieuwe lijst (list) teruggeven, die aangeeft in welke volgorde we de gegeven items initieel op een stapel moeten leggen om ze in de gevraagde volgorde te delen.
Voorbeeld
>>> delen((0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10))
[0, 2, 4, 6, 8, 10, 3, 7, 1, 9, 5]
>>> delen([0, 8, 1, 6, 2, 10, 3, 7, 4, 9, 5])
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> delen('ABCDEFGHIJKLMOP')
['A', 'C', 'E', 'G', 'I', 'K', 'M', 'P', 'D', 'H', 'L', 'B', 'J', 'F', 'O']
>>> delen('ALBICODJEMFKGPH')
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'O', 'P']
>>> polka((0, 2, 4, 6, 8, 10, 3, 7, 1, 9, 5))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> polka([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
[0, 8, 1, 6, 2, 10, 3, 7, 4, 9, 5]
>>> polka('ACEGIKMPDHLBJFO')
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'O', 'P']
>>> polka('ABCDEFGHIJKLMOP')
['A', 'L', 'B', 'I', 'C', 'O', 'D', 'J', 'E', 'M', 'F', 'K', 'G', 'P', 'H']
Epiloog
Math for Love1 is een organisatie uit Seattle (Verenigde Staten) die het wiskunde-onderwijs wil hervormen door middel van puzzels, spelletjes en het organiseren van workshops voor leerkrachten. In 2014 startten ze een geldinzamelingscampagne op Kickstarter2 om de kaartenset Tiny Polka Dot op de markt te kunnen brengen, waarmee leerkrachten hun kleuters en kinderen kunnen uitdagen om verschillende puzzels op te lossen. In een voordracht voor Ted Talks geeft Daniel Finkel van Math for Love aan waar het de organisatie om te doen is:
De oudste versie van de Polka Dot puzzel is terug te vinden onder de naam The Nun's Puzzle3 in het boek The Canterbury Puzzles4 uit 1907, geschreven door Henry Dudeney. Dudeney zegt erbij dat de puzzel heel eenvoudig op te lossen is als je gebruiktmaakt van echte kaarten, en stelt daarom voor om hem zonder kaarten te proberen oplossen.
Bronnen
-
Burns M (1982). Math for Smarty Pants. Little Brown Books for Young Readers. 5
-
Dudeney HE (1907). The Canterbury Puzzles and Other Curious Problems. Thomas Nelson and Sons, LTD., London, Edinburgh and New York. 6
-
Stenmark JK, Thompson V, Cossey R, Hill M (1986). Family Math. Lawrence Hall of Science. 7