Een wirwar van getallen. Zo komen macro-economische cijfers op de meeste mensen over. Zie daar maar eens een onregelmatigheid of een foutje in te ontdekken. Jarenlang kon de Griekse overheid de EU misleiden met haar macro-economische cijfers. De Grieken hadden de schijnbaar perfecte fraude ontdekt: simpel uit te voeren en moeilijk traceerbaar. De overheid stelde haar macro-economische gegevens vast, maar paste hier en daar een vervelend getal aan. De gegevens stuurden ze vervolgens naar Eurostat, het Europese statistiekagentschap, om te bewijzen dat Griekenland voldeed aan het stabiliteitspact van de EU. Geen haan die ernaar kraaide, vooral omdat het controleren van macro-economische cijfers — samenvattingen van complexe economische processen — een bijzonder ingewikkelde taak is.

Economen die nationale boekhoudingen controleren, krijgen echter hulp uit onverwachte hoek. Een wiskundige curiositeit, genaamd de wet van Benford¹, lijkt financieel gesjoemel genadeloos aan het licht te brengen — zonder getallen tot in den treure na te lopen. De wet schrijft voor dat in de begincijfers van natuurlijke getallen een bepaalde regelmaat is te ontdekken. De meest uiteenlopende gegevens, van aandelen tot oppervlakten van meren en van priemgetallen tot biedingen op eBay, allemaal vertonen ze hetzelfde patroon. Verrassend vaak is het begincijfer van dergelijke getallen een 1, namelijk bij ongeveer één op de drie getallen. Iets minder vaak is het begincijfer 2, nog iets minder vaak 3 enzovoort.

De 'natuurlijke' verdeling van begincijfers is tot in detail vastgelegd in het originele artikel uit 1937 dat de wet van Benford beschrijft. Hierin wordt gesteld dat de kans $$P(c)$$ dat een natuurlijk getal begint met het cijfer $$c$$ gelijk is aan
\[ P(c) = \log_{10}\left(1 + \frac{1}{c}\right) \]
Deze kans wordt grafisch weergegeven in onderstaande figuur.

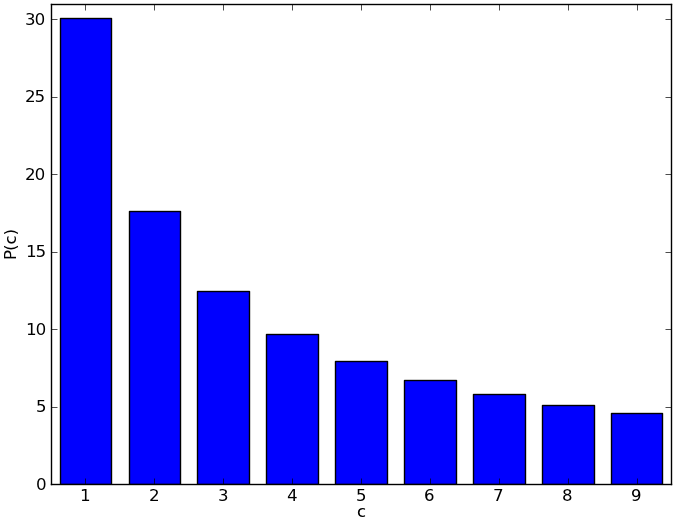
Wijkt een reeks getallen van dit patroon af, dan is de reeks waarschijnlijk niet op een natuurlijke manier tot stand gekomen — of mogelijk aangepast.

Opgave

Schrijf een functie benford die de theoretische kans $$P(c)$$ teruggeeft dat een natuurlijk getal begint met het cijfer $$c$$. Deze kans moet uitgedrukt worden als een percentage. Het cijfer $$c$$ moet als argument aan de functie doorgegeven worden.
Schrijf een functie leesData waaraan de locatie van een tekstbestand moet doorgegeven worden als eerste verplichte argument. Alle regels van dit tekstbestand moeten eenzelfde aantal informatievelden bevatten die telkens van elkaar gescheiden worden door één enkel scheidingskarakter. De functie moet als resultaat de lijst van integerwaarden teruggeven, die de waarden uit een gegeven kolom van het tekstbestand bevat. Deze kolom (veldnummers worden geteld vanaf 1) moet als tweede verplicht argument aan de functie doorgegeven worden. Indien het opgegeven veld van het tekstbestand reële getallen bevat, dan moeten deze afgerond worden naar de dichtstbijzijnde integerwaarde. Optioneel kan een derde argument aan de functie doorgegeven worden: het scheidingskarakter dat gebruikt wordt om de informatievelden in het tekstbestand van elkaar te scheiden. Gebruik een tab als standaardwaarde voor dit optioneel argument.
Schrijf een functie testBenford die kan gebruikt worden om na te gaan of een gegeven lijst van integerwaarden (die als argument aan de functie doorgegeven wordt) voldoet aan de wet van Benford. Voor elk cijfer $$c$$ van 1 tot en met 9 moet de functie op een afzonderlijk regel eerst het cijfer $$c$$ zelf uitschrijven, gevolgd door de theoretische kans $$P(c)$$ (als percentage) dat een natuurlijk getal begint met het cijfer $$c$$ en het percentage van de integerwaarden in de gegeven lijst die beginnen het cijfer $$c$$. Beide percentages worden telkens rechts uitgelijnd over 8 posities, en worden weergegeven afgerond tot op twee cijfers na de komma.

Voorbeeld

Het bestand meren.txt² bevat een lijst van alle meren in de Amerikaanse staat Minnesota. Minnesota wordt ook wel The Land of 10.000 Lakes genoemd, maar een officiële telling geeft aan dat er ongeveer 11.842 meren zijn met een totale oppervlakte van 40.000 $$\text{m}^2$$. Voor elk meer bevat het bestand op een afzonderlijke regel de volgende informatievelden, die van elkaar gescheiden worden door een komma: i) naam, ii) provincie, iii) nabijgelegen stad, iv) totale oppervlakte (in acre), v) oppervlakte getijdenzone (in acre), vi) maximale diepte (in voet) en vii) troebelheid (in voet). Ook voor deze gegevens geldt de Wet van Benford, zoals blijkt uit onderstaande interactieve Pythonsessie (met de oppervlate van de getijdenzone als voorbeeld).

>>> benford(3)
12.4938736608
>>> benford(7)
5.79919469777

>>> oppervlakte = leesData('meren.txt', 5, ',')
>>> oppervlakte
[417, 269, 424, 238, 453, 2654, 96, ..., 1953, 367, 432, 345, 387, 89]
>>> testBenford(oppervlakte)
1   30.10   31.81
2   17.61   20.55
3   12.49   12.51
4    9.69    9.29
5    7.92    6.61
6    6.69    6.17
7    5.80    5.00
8    5.12    4.47
9    4.58    3.57

Voorbeeld

Onderstaande interactieve Pythonsessie maakt gebruik van het bestand inwoners.txt³. Dit is een tekstbestand dat bestaat uit twee kolommen (van elkaar gescheiden door een tab): i) de naam en ii) het aantal inwoners van een land.

>>> data = leesData('inwoners.txt', 2)
>>> data
[33609937, 3639453, 34178188, ..., 48508972, 9059651, 7604467]
>>> testBenford(data)
1   30.10   25.11
2   17.61   16.88
3   12.49   11.69
4    9.69   14.29
5    7.92    5.19
6    6.69    8.23
7    5.80    7.36
8    5.12    6.93
9    4.58    4.33