Experiment
-
Stel dat we geen toegang hebben tot de metingen van de NHANES studie.
-
We zouden dan een experiment op moeten zetten om metingen bij mannen en vrouwen te doen.
-
Veronderstel dat we budget hebben om metingen bij 5 mannen en 5 vrouwen te doen.
-
We zouden dan 5 mannen en 5 vrouwen boven de 25 jaar at random selecteren uit de Amerikaanse populatie.
-
We kunnen dit experiment simuleren door 5 vrouwen en 5 mannen at random te selecteren uit de NHANES studie.
Code
1. het `set.seed` commando wordt gebruikt omdat we dezelfde steekproef zou trekken als we de code opnieuw laten lopen. Dit is louter om de cursus consistent te houden als we de nota's opnieuw maken.
2. het nSamp object bevat de steekproefgrootte per groep
3. we trekken 5 vrouwelijke subjecten uit de nhanesSub dataset
4. vervolgens trekken we 5 mannen uit de nhanesSub dataset
5. we voegen de data van mannen en vrouwen samen in 1 dataset. Het `rbind` commando zal de data van de rijen onder elkaar zetten.
6. We tonen de dataset
set.seed(1023)
nSamp <- 5
fem <- nhanesSub %>%
filter(Gender=="female") %>%
sample_n(size=5)
mal <- nhanesSub %>%
filter(Gender=="male") %>%
sample_n(size=5)
samp1 <- rbind(fem,mal)
samp1
## # A tibble: 10 × 2
## Gender Height
## <fct> <dbl>
## 1 female 164
## 2 female 160.
## 3 female 159
## 4 female 154.
## 5 female 156.
## 6 male 170.
## 7 male 183.
## 8 male 183.
## 9 male 185.
## 10 male 170.
We hebben met de code dus een steekproef getrokken van 5 vrouwen en 5 mannen. We exploreren vervolgens de data in de steekproef.
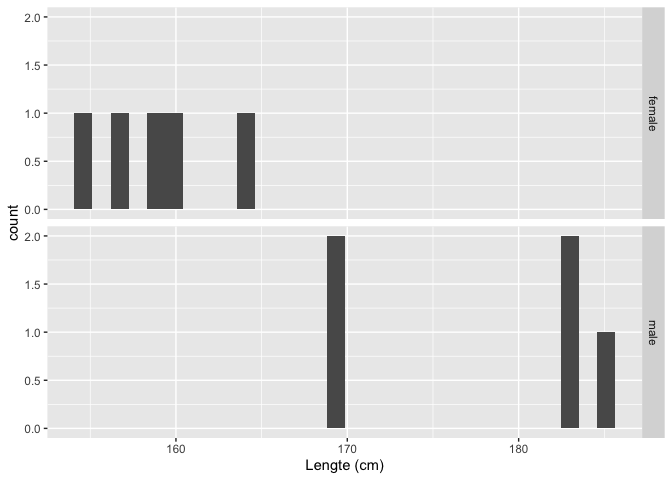
Code
samp1 %>%
ggplot(aes(x=Height)) +
geom_histogram() +
facet_grid(Gender~.) +
xlab("Lengte (cm)")
HeightSumExp1 <- samp1 %>%
group_by(Gender) %>%
summarize_at("Height",
list(mean = mean,
sd = sd)
)
HeightSumExp1
## # A tibble: 2 × 3
## Gender mean sd
## <fct> <dbl> <dbl>
## 1 female 159. 3.76
## 2 male 178. 7.55
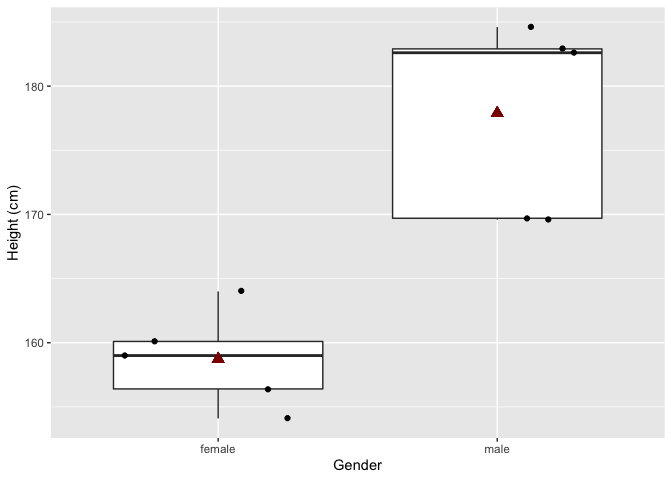
Histogram is niet zinvol als we maar zo weinig datapunten hebben. Een boxplot is meer geschikt om distributies te vergelijken als er weinig data zijn:
Einde Code
Om na te gaan of het verschil in de steekproef groot genoeg is om de bevindingen van de steekproef te kunnen veralgemenen naar de populatie toe voeren we opnieuw een t-test uit.
Met de p-waarde wordt de kans berekend om in een nieuwe random steekproef door toeval een effect te vinden dat in absolute waarde minstens evengroot is als in onze geobserveerde steekproef onder de aanname dat er in werkelijkheid geen verschil zou zijn in gemiddelde lengte tussen vrouwen en mannen.
Als die kans heel klein is is het weinig waarschijnlijk om onze steekproef te observeren onder de hypothese dat de lengtes gemiddeld niet verschillen tussen vrouwen en mannen en kunnen we deze hypothese verwerpen.
Typisch wordt de kans op een valse positieve conclusie gecontroleerd op 5%.
t.test(Height~Gender,data=samp1)
##
## Welch Two Sample t-test
##
## data: Height by Gender
## t = -5.0783, df = 5.8695, p-value = 0.00242
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## -28.441927 -9.878073
## sample estimates:
## mean in group female mean in group male
## 158.72 177.88
In het experiment zijn vrouwen gemiddeld 19.16 cm kleiner dan mannen. En als we een statistische test uitvoeren (zie hoofdstuk 5: Statistische besluitvorming) kunnen we besluiten dat dit verschil statistisch significant is.
Herhaal het experiment
Als we het experiment herhalen selecteren we andere mensen en verkrijgen we andere resultaten.
set.seed(1024)
fem <- nhanesSub %>%
filter(Gender=="female") %>%
sample_n(size=5)
mal <- nhanesSub %>%
filter(Gender=="male") %>%
sample_n(size=5)
samp2 <- rbind(fem,mal)
HeightSumExp2 <- samp2 %>%
group_by(Gender) %>%
summarize_at("Height",
list(mean=mean,
sd=sd)
)
HeightSumExp2
## # A tibble: 2 × 3
## Gender mean sd
## <fct> <dbl> <dbl>
## 1 female 166. 9.89
## 2 male 170. 8.24
samp2 %>%
ggplot(aes(x = Gender,y = Height)) +
geom_boxplot(outlier.shape = NA) +
geom_point(position = "jitter") +
geom_point(
aes(x = 1, y = HeightSumExp2$mean[1]),
size = 3,
pch = 17,
color="darkred") +
geom_point(
aes(x = 2, y = HeightSumExp2$mean[2]),
size = 3,
pch = 17,
color = "darkred") +
ylab("Height (cm)")
t.test(Height ~ Gender, data=samp2)
##
## Welch Two Sample t-test
##
## data: Height by Gender
## t = -0.7295, df = 7.747, p-value = 0.4872
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## -17.552343 9.152343
## sample estimates:
## mean in group female mean in group male
## 166.26 170.46
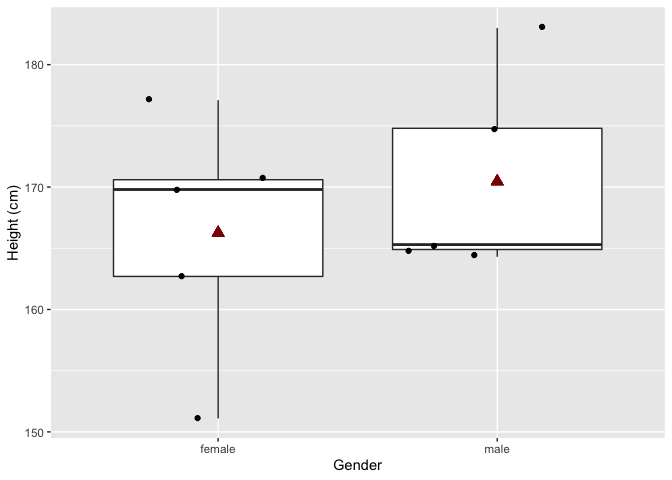
Vijf andere mannen en vrouwen worden getrokken uit de populatie. Hierdoor verschillen de lengte metingen van de vorige steekproef alsook de berekende gemiddeldes en de p-waarde van de statistische toets.
In de nieuwe steekproef zijn vrouwen gemiddeld 4.2 cm kleiner dan mannen. En dit verschil is statistisch niet significant
Herhaal het experiment opnieuw
seed <- 88605
set.seed(seed)
fem <- nhanesSub %>%
filter(Gender=="female") %>%
sample_n(size=5)
mal <- nhanesSub %>%
filter(Gender=="male") %>%
sample_n(size=5)
samp3 <- rbind(fem,mal)
HeightSumExp3 <- samp3 %>%
group_by(Gender) %>%
summarize_at("Height",
list(mean=mean,
sd=sd)
)
HeightSumExp3
## # A tibble: 2 × 3
## Gender mean sd
## <fct> <dbl> <dbl>
## 1 female 173. 1.97
## 2 male 168. 2.84
samp3 %>%
ggplot(aes(x = Gender,y = Height)) +
geom_boxplot(outlier.shape = NA) +
geom_point(position = "jitter") +
geom_point(
aes(x = 1, y = HeightSumExp3$mean[1]),
size = 3,
pch = 17,
color="darkred") +
geom_point(
aes(x = 2, y = HeightSumExp3$mean[2]),
size = 3,
pch = 17,
color = "darkred") +
ylab("Height (cm)")
t.test(Height ~ Gender, data=samp3)
##
## Welch Two Sample t-test
##
## data: Height by Gender
## t = 3.1182, df = 7.136, p-value = 0.01648
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## 1.178916 8.461084
## sample estimates:
## mean in group female mean in group male
## 172.60 167.78
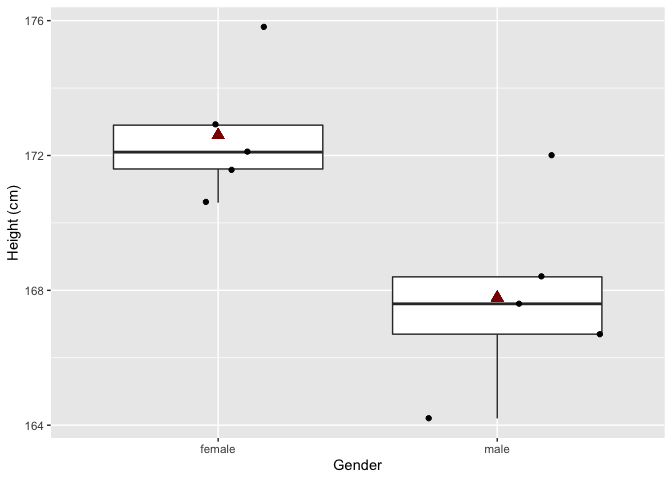
In de nieuwe steekproef zijn vrouwen gemiddeld 4.82 cm groter dan mannen. En dit verschil is statistisch significant
Merk op dat we in deze extreme steekproef door toeval vrij grote vrouwen en eerder kleine mannen hebben getrokken uit de populatie. Een dergelijke steekproef zal eerder zeldzaam zijn maar kan door toeval voorkomen.
In de onderstaande paragraaf leggen we uit hoe we deze extreme steekproef hebben bekomen:
Een seed wordt in de cursus gebruikt om ervoor te zorgen dat we telkens dezelfde resultaten bekomen als we de random generator opnieuw laten lopen in R (zie het set.seed commando). Dat doen we puur om de resultaten in de cursus gelijk te kunnen houden als we aanpassingen hebben doorgevoerd aan de tekst en de code dus opnieuw moeten laten lopen om de cursus te compileren. In vrijwel alle code is de seed gewoon random gekozen.
Om de extreme steekproef weer te geven, hebben we deze keer echter geen random seed gebruikt. Daarvoor hebben we alle seeds overlopen van 1 tot 100000. We hebben dus 8.8605^{4} steekproeven moeten trekken alvorens we een dergelijke extreme steekproef uit de populatie hadden getrokken waaruit we ten onrechte zouden concluderen dat vrouwen gemiddeld significant groter zijn dan mannen.
Samenvatting
We trokken at random andere proefpersonen in elke steekproef. Hierdoor
-
verschillen de lengtemetingen van steekproef tot steekproef.
-
Dus ook de geschatte gemiddeldes en standaard deviaties.
-
Bijgevolg zijn onze conclusies ook onzeker en kunnen deze wijzigen van steekproef tot steekproef.
-
Ook steekproeven waarbij het effect tegengesteld is aan dat in de populatie en waarbij we besluiten dat het verschil significant is kunnen voorkomen.
-
We kunnen aantonen dat dergelijke steekproeven voor experimenten waarbij we de lengte tussen mannen en vrouwen vergelijken eerder zeldzaam zijn.
\(\rightarrow\) Met statistiek gaan we de kans op het trekken foute conclusies controleren.