Now consider a situation in which the two classes are linearly separable. Then we can find a separating hyperplane using the svm() function. We first further separate the two classes in our simulated data so that they are linearly separable:

x[y == 1,] <- x[y == 1,] + 0.5
plot(x, col = (y + 5) / 2, pch = 19)

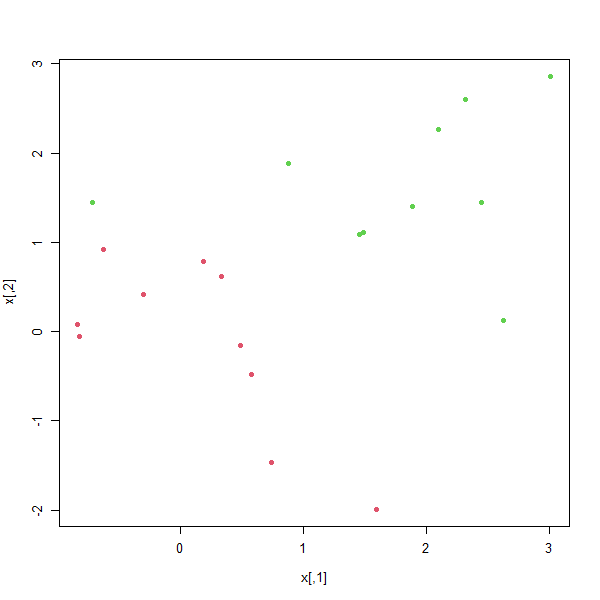
Now the observations are just barely linearly separable. We fit the support vector classifier and plot the resulting hyperplane, using a very large value of cost so that no training observations are misclassified.

dat <- data.frame(x = x, y = as.factor(y))
svmfit <- svm(y ~ ., data = dat, kernel = "linear", cost = 1e5)
summary(svmfit)
Call:
svm(formula = y ~ ., data = dat, kernel = "linear", 
    cost = 1e+05)
Parameters:
   SVM-Type:  C-classification 
 SVM-Kernel:  linear 
       cost:  1e+05 
Number of Support Vectors:  3
 ( 1 2 )
Number of Classes:  2 
Levels: 
 -1 1

plot(svmfit, dat)

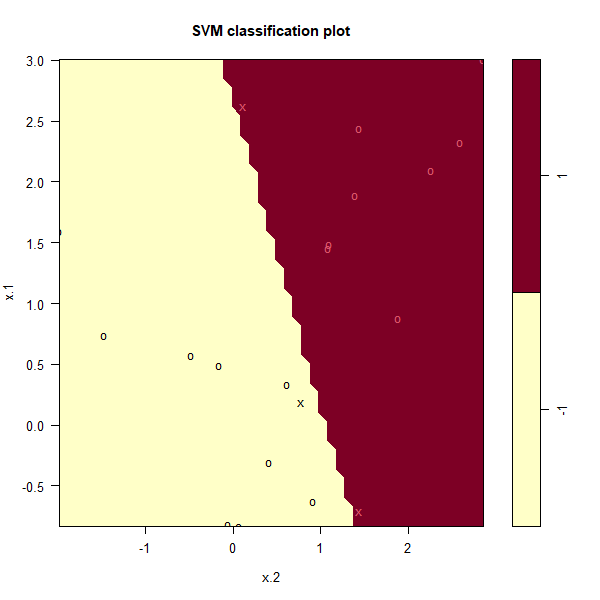
Note: The axis are swapped compared to the previous graph

No training errors were made and only three support vectors were used. However, we can see from the figure that the margin is very narrow (because the observations that are not support vectors, indicated as circles, are very close to the decision boundary). It seems likely that this model will perform poorly on test data. We now try a smaller value of cost:

svmfit <- svm(y ~ ., data = dat, kernel = "linear", cost = 1)
summary(svmfit)
plot(svmfit, dat)

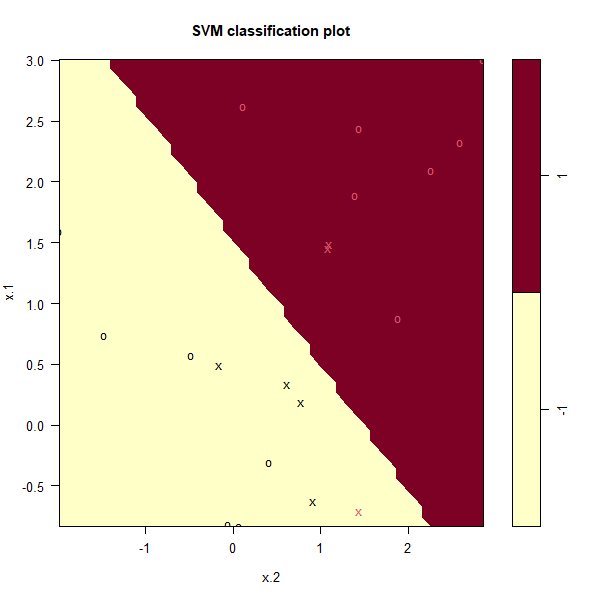
Using cost=1, we misclassify a training observation, but we also obtain a much wider margin and make use of seven support vectors.

MC1: Which model would most likely perform better on test data
1) Model with cost = 1
2) Model with cost = 1e5