Next, we consider whether pruning the tree might lead to improved results. The function cv.tree() performs cross-validation in order to determine the optimal level of tree complexity; cost complexity pruning is used in order to select a sequence of trees for consideration. We use the argument FUN=prune.misclass in order to indicate that we want the classification error rate to guide the cross-validation and pruning process, rather than the default for the cv.tree() function, which is deviance. 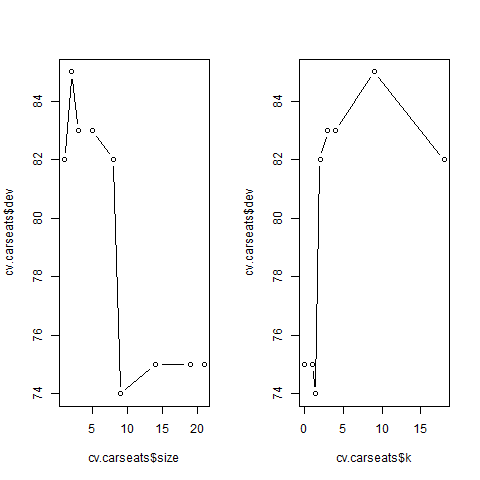The cv.tree() function reports the number of terminal nodes of each tree considered (size) as well as the corresponding error rate and the value of the cost-complexity parameter used (k, which corresponds to \(\alpha\) in \(\sum_{m=1}^{| T |} \sum_{x_i \in R_m} (y_i - \hat{y}_{R_m})^2 + \alpha |T|\)).

set.seed(7)
cv.carseats <- cv.tree(tree.carseats, FUN = prune.misclass)
names(cv.carseats)
[1] "size"   "dev"    "k"      "method"

cv.carseats
$size
[1] 21 19 14  9  8  5  3  2  1

$dev
[1] 75 75 75 74 82 83 83 85 82
$k
[1] -Inf  0.0  1.0  1.4  2.0  3.0  4.0  9.0 18.0

$method
[1] "misclass"

attr(,"class")
[1] "prune"         "tree.sequence"

Note that, despite the name, dev corresponds to the cross-validation error rate in this instance. The tree with 9 terminal nodes results in the lowest cross-validation error rate, with 74 cross-validation errors.We plot the error rate as a function of both size and k.

par(mfrow = c(1, 2))
plot(cv.carseats$size, cv.carseats$dev, type = "b")
plot(cv.carseats$k, cv.carseats$dev, type = "b")

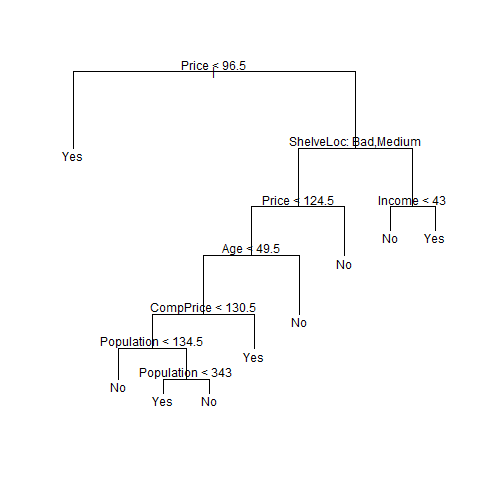
We now apply the prune.misclass() function in order to prune the tree to obtain the nine-node tree.

prune.carseats <- prune.misclass(tree.carseats, best = 9)
plot(prune.carseats)
text(prune.carseats, pretty = 0)

How well does this pruned tree perform on the test data set? Once again, we apply the predict() function.

tree.pred <- predict(prune.carseats, Carseats.test, type = "class")
table(tree.pred, High.test)
         High.test
tree.pred No Yes
      No  97  25
      Yes 20  58
      
(97 + 58) / 200
[1] 0.775

Now 77.5% of the test observations are correctly classified, so not only has the pruning process produced a more interpretable tree, but it has also improved the classification accuracy.

Questions

• Increase the value of best to 15 in the prune.misclass() function, so we obtain a larger pruned tree. Store the result in the variable prune.carseats.
• Use the tree to make class predictions on the test set. Store the predictions in the variable tree.pred.
• Calculate the confusion matrix. (note: give the predictions as the first argument in the table() function, and the ground truth as the second argument). Store the result in the variable cf.test.
• Finally, calculate the test set accuracy. Store the result in the variable acc.test.
  (note: try to avoid hardcoding and use e.g. the sum() and diag() functions on the confusion matrix)

Below, you find the necessary variables.

Assume that:

• The ISLR2 and tree libraries have been loaded
• The Carseats dataset has been loaded and attached