De liftparadox is een paradox die rond 1950 voor het eerst werd opgemerkt door Moritz Stern en George Gamow. Beide fysici hadden hun kantoor op verschillende verdiepingen van hetzelfde gebouw. Gamow had een kantoor op de tweede verdieping en merkte op dat de eerste lift die stopte op zijn verdieping doorgaans op weg was naar beneden. Stern had een kantoor op één van de hoogste verdiepingen en merkte op dat de eerste lift die stopte op zijn verdieping doorgaans naar boven ging.

Op het eerste gezicht leek dit de indruk te wekken dat er ergens in het midden van het gebouw liften gefabriceerd werden die ofwel naar boven of naar beneden gestuurd werden om terug afgebroken te worden op het dak of in de kelder. Dat was natuurlijk niet het geval, en dus moest er wel een logische verklaring zijn voor dit fenomeen.
Stel dat we ons bijvoorbeeld op één van de onderste verdiepingen bevinden. In dat geval zal de lift het grootste deel van zijn tijd doorbrengen op de verdiepingen boven ons. Als we op een willekeurig tijdstip op de lift gaan wachten, dan is het dus meest waarschijnlijk dat de eerstvolgende lift die op onze verdieping passeert van boven toekomt en naar beneden zal gaan. Het omgekeerde is het geval als we ons op één van de bovenste verdiepingen bevinden.
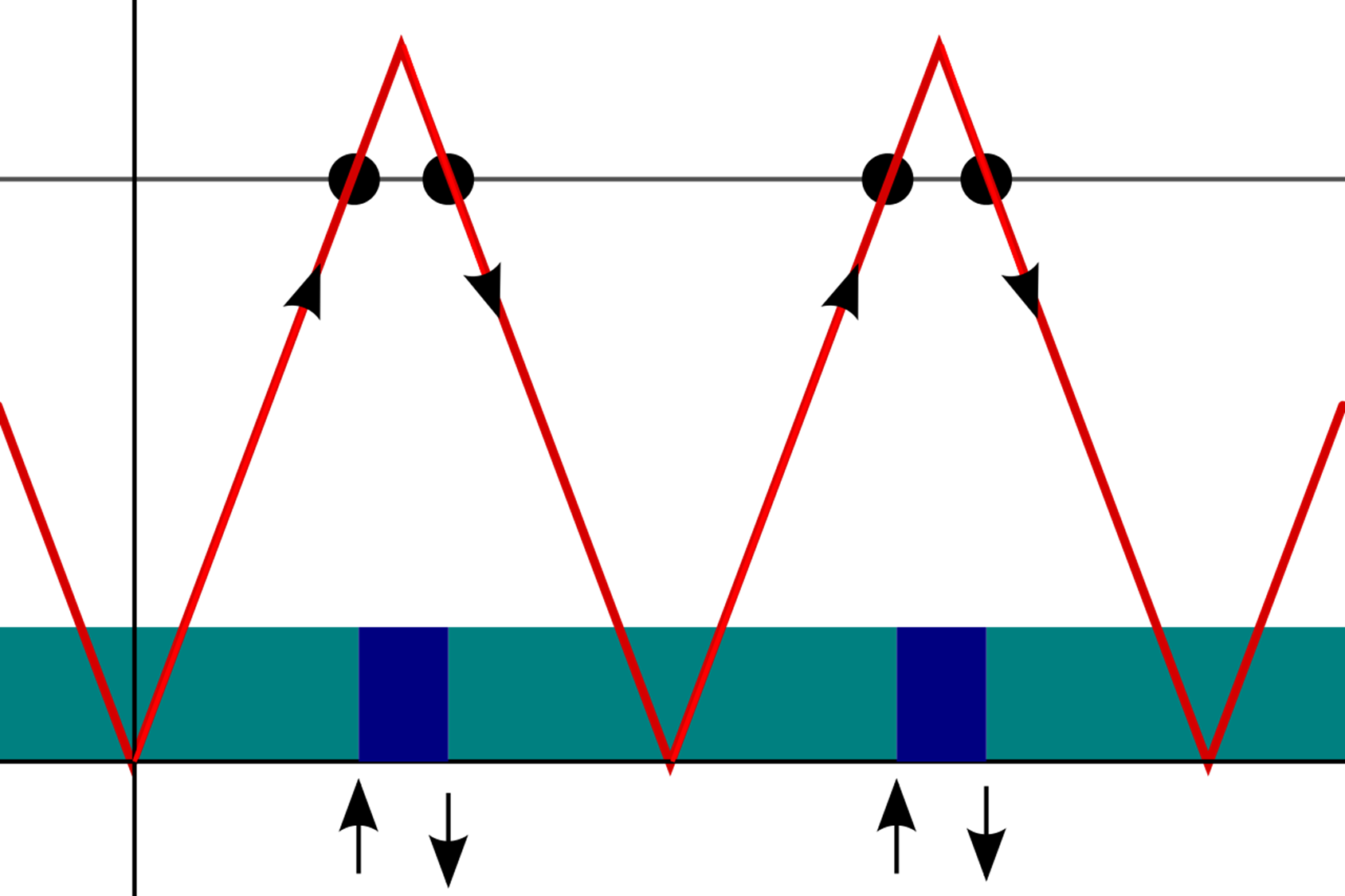
Om het wat concreter te maken, beschouwen we een gebouw met dertig verdiepingen — plus het gelijkvloers — waarin slechts één trage lift beschikbaar is. De lift is zo traag omdat ze op elke verdieping stopt op weg naar boven, en daarna terug op elke verdieping stopt op weg naar beneden. In totaal duurt het één minuut om van een verdieping naar de volgende verdieping te gaan en te wachten tot alle passagiers zijn in- of uitgestapt. Hieronder staat het tijdsschema voor de personen die het ongeluk hebben om in dit gebouw te werken. Zoals ook al bleek uit bovenstaande figuur vormt het traject van de lift een driehoeksgolf.
| verdieping | lift naar boven | lift naar beneden |
|---|---|---|
| gelijkvloers | 8:00, 9:00, … | nvt |
| 1e verdieping | 8:01, 9:01, … | 8:59, 9:59, … |
| 2e verdieping | 8:02, 9:02, … | 8:58, 9:58, … |
| … | … | … |
| 29e verdieping | 8:29, 9:29, … | 8:31, 9:31, … |
| 30e verdieping | nvt | 8:30, 9:30, … |
Als je je bijvoorbeeld op de eerste verdieping van dit gebouw bevindt en op een willekeurig tijdstip naar de lift zou stappen, dan is de kans groot dat de eerstvolgende lift die toekomt op weg is naar beneden. De eerstvolgende lift gaat enkel naar boven tijdens de eerste twee minuten na het uur, bijvoorbeeld om 9:00 en 9:01. Het aantal plaatsen waar de lift stopt op weg naar boven en op weg naar beneden mag dan wel hetzelfde zijn, de kans dat de volgende lift naar boven gaat is slechts 2 op 60.
Opgave
Stel een tijdsschema op van een trage lift die elke verdieping aandoet en er telkens één minuut over doet om naar de volgende verdieping te gaan. Bij aanvang van de simulatie bevindt de lift zich op een bepaalde verdieping en beweegt in een bepaalde richting. Nadat de lift het gelijkvloers bereikt heeft, gaat ze terug naar boven. Nadat de lift de hoogste verdieping bereikt heeft, zal ze terug naar beneden gaan.
Invoer
Zeven regels die achtereenvolgens de volgende informatie bevatten die je moet gebruiken om het traject van de lift te simuleren:
-
aantal stappen in de simulatie ($$\in \mathbb{N}$$); elke verdieping die door de lift bezocht wordt — inclusief de startverdieping — vormt één enkele stap in de simulatie
-
nummer $$i \in \mathbb{N}$$ ($$0 \le i \le k$$) van de verdieping waarop de simulatie start; gelijkvloers krijgt nummer 0
-
nummer $$k \in \mathbb{N}_0$$ van de hoogste verdieping
-
karakter dat aangeeft of de lift naar boven of naar beneden gaat bij aanvang van de simulatie; een hoedje (accent circonflexe; ^) geeft aan dat de lift initieel naar boven gaat; de letter v geeft aan dat de lift initieel naar beneden gaat
-
aantal uren op een 24-uursklok bij aanvang van de simulatie; bijvoorbeeld 23 wanneer de simulatie start om 23:14
-
aantal minuten op een 24-uursklok bij aanvang van de simulatie; bijvoorbeeld 14 wanneer de simulatie start om 23:14
-
tekst die aangeeft hoe gedetailleerd de informatie over de simulatie moet uitgeschreven worden; de tekst alles geeft aan dat er voor elke stap informatie moet uitgeschreven worden; de tekst stil geeft aan dat er enkel informatie moet uitgeschreven worden als de lift zich op verdieping $$i$$ bevindt
Uitvoer
De lift start op verdieping $$i$$ en beweegt in de opgegeven richting. Voor elke verdieping die in het tijdschema moet opgenomen worden, wordt er een regel uitgeschreven met het tijdstip, het nummer van de verdieping en de beweginsrichting (^ als de lift vanaf deze verdieping naar boven gaat en v als de lift vanaf deze verdieping naar beneden gaat). Leid het formaat van de uitvoer af uit onderstaande voorbeelden. Als de laatste regel van de invoer de tekst alles bevat, dan moeten alle verdiepingen die de lift tijdens de simulatie aandoet in het tijdsschema opgenomen worden. Als de laatste regel van de invoer de tekst stil bevat, dan moet enkel de startverdieping $$i$$ in het tijdsschema opgenomen worden.
Voorbeeld
Invoer:
30
6
8
^
23
50
allesUitvoer:
23:50 6 [^]
23:51 7 [^]
23:52 8 [v]
23:53 7 [v]
23:54 6 [v]
23:55 5 [v]
23:56 4 [v]
23:57 3 [v]
23:58 2 [v]
23:59 1 [v]
00:00 0 [^]
00:01 1 [^]
00:02 2 [^]
00:03 3 [^]
00:04 4 [^]
00:05 5 [^]
00:06 6 [^]
00:07 7 [^]
00:08 8 [v]
00:09 7 [v]
00:10 6 [v]
00:11 5 [v]
00:12 4 [v]
00:13 3 [v]
00:14 2 [v]
00:15 1 [v]
00:16 0 [^]
00:17 1 [^]
00:18 2 [^]
00:19 3 [^]Voorbeeld
Invoer:
30
6
8
v
9
30
stilUitvoer:
09:30 6 [v]
09:42 6 [^]
09:46 6 [v]
09:58 6 [^]