De cellen van een rechthoekig $$m \times n$$ rooster met $$m$$ rijen en $$n$$ kolommen bevatten elk een getal van 0 tot en met 9. Op die manier ontstaan groepen van aangrenzende cellen die allemaal hetzelfde getal bevatten, waarbij cellen aan elkaar grenzen als ze een gemeenschappelijke zijde hebben (horizontaal of verticaal). Onderstaand $$4 \times 4$$ rooster heeft bijvoorbeeld vijf groepen die elk met eigen kleur aangeduid worden.

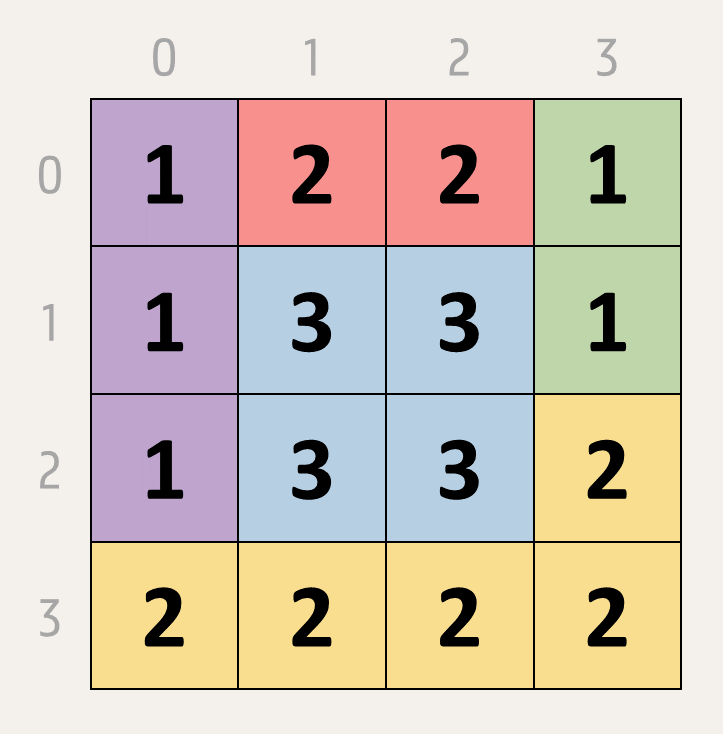
In één zet worden de getallen in alle cellen van een groep met 1 verhoogd of verlaagd, waardoor de groep kan samensmelten met andere groepen. Hierbij mag de waarde in de cellen nooit kleiner worden dan 0 of groter dan 9. De uitdaging bestaat erin om met een minimum aan zetten alle cellen van het rooster tot één enkele groep te laten samensmelten. Voor het rooster hierboven volstaan twee zetten:

• verlaag alle cellen van de blauwe groep in het midden van het rooster, waardoor die samensmelt met de rode en de gele groep

• verlaag alle cellen van de nieuwe grotere groep, waardoor die samensmelt met de paarse en de groene groep

Opgave

De lijstvoorstelling van een reeks cijfers die gerangschikt zijn in een rechthoekig $$m \times n$$ rooster bestaat uit een lijst (list) met de $$m$$ rijen van het rooster (van boven naar beneden), waarbij elk rij zelf ook voorgesteld wordt als een lijst (list) met de $$n$$ getallen (int) op de rij (van links naar rechts).

De stringvoorstelling van een reeks cijfers die gerangschikt zijn in een rechthoekig $$m \times n$$ rooster bestaat uit een tuple met drie elementen: i) een string (str) met de cijfers in het rooster uitgelezen van links naar rechts en van boven naar onder, ii) het aantal rijen (int) van het rooster en iii) het aantal kolommen (int) van het rooster.

We nummeren de rijen van het rooster van boven naar onder vanaf nul. Analoog nummeren we ook de kolommen van links naar rechts vanaf nul. Op die manier kan de positie van een cel in het rooster voorgesteld worden door een tuple $$(r, k)$$, waarbij $$r$$ en $$k$$ het nummer van de rij en de kolom aangeven waarop de cel terug te vinden is in het rooster.

Gevraagd wordt:

• Schrijf een functie lijstvoorstelling waaraan drie argumenten moeten doorgegeven worden die corresponderen met de drie afzonderlijke elementen uit de stringvoorstelling van een rooster. Het derde argument mag weggelaten worden bij vierkante roosters (waarbij het aantal rijen en kolommen gelijk zijn). De functie moet de lijstvoorstelling van het gegeven rooster teruggeven.

• Schrijf een functie stringvoorstelling waaraan de lijstvoorstelling van een rooster moet doorgegeven worden. De functie moet de stringvoorstelling van het gegeven rooster teruggeven.

• Schrijf een functie zet waaraan drie argumenten moeten doorgegeven worden: i) een getal $$\alpha \in \mathbb{N}$$ (int), ii) een verzameling (set) met posities van cellen in een rooster en iii) de lijstvoorstelling van het rooster. De functie moet de waarde $$\alpha$$ optellen bij alle aangegeven cellen van het rooster, en moet een verwijziging naar het gegeven rooster teruggeven.

• Schrijf een functie is_opgelost waaraan de lijstvoorstelling van een rooster moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of alle cellen in het gegeven rooster dezelfde waarde bevatten.

• Schrijf een functie groep waaraan twee argumenten moeten doorgegeven worden: i) de positie van een cel in een rooster en ii) de lijstvoorstelling van het rooster. De functie moet een verzameling (set) teruggeven met de posities van alle cellen in de groep die de gegeven cel bevat.

• Schrijf een functie is_oplossing waaraan twee argumenten moeten doorgegeven worden: i) een lijst (list) met zetten en ii) de lijstvoorstelling van een rooster. Elke zet wordt voorgesteld door een tuple $$(r, k, b)$$, waarbij $$(r, k)$$ de positie aanduidt van een cel in de groep die moet verhoogd of verlaagd worden, en $$b$$ een Booleaanse waarde (bool) is die aangeeft of de groep moet verhoogd (True) of verlaagd (False) worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of het uitvoeren van de zetten resulteert in een rooster waarvan alle cellen dezelfde waarde bevatten.

De functies stringvoorstelling, is_opgelost, groep en is_oplossingen mogen het rooster dat eraan doorgegeven wordt niet wijzigen. De functie zet daarentegen moet de waarden in het gegeven rooster zelf aanpassen, en een verwijziging naar het gegeven rooster teruggeven.

Voorbeeld

>>> rooster = lijstvoorstelling('1221133113322222', 4)
>>> rooster
[[1, 2, 2, 1], [1, 3, 3, 1], [1, 3, 3, 2], [2, 2, 2, 2]]
>>> stringvoorstelling(rooster)
('1221133113322222', 4, 4)
>>> zet(-1, {(1, 2), (1, 1), (2, 1), (2, 2)}, rooster)
[[1, 2, 2, 1], [1, 2, 2, 1], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> rooster
[[1, 2, 2, 1], [1, 2, 2, 1], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> zet(+1, {(0, 3), (1, 3)}, rooster)
[[1, 2, 2, 2], [1, 2, 2, 2], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> rooster
[[1, 2, 2, 2], [1, 2, 2, 2], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> zet(+1, {(2, 0), (1, 0), (0, 0)}, rooster)
[[2, 2, 2, 2], [2, 2, 2, 2], [2, 2, 2, 2], [2, 2, 2, 2]]
>>> is_opgelost(rooster)
True

>>> rooster = lijstvoorstelling('1221133113322222', 4)
>>> groep((2, 1), rooster)
{(1, 2), (1, 1), (2, 1), (2, 2)}
>>> groep((0, 3), rooster)
{(0, 3), (1, 3)}
>>> groep((1, 0), rooster)
{(2, 0), (1, 0), (0, 0)}
>>> is_oplossing([(1, 1, False), (3, 2, False)], rooster)
True
>>> is_oplossing([(1, 3, True), (3, 2, False), (0, 1, True)], rooster)
False