Vis viva (Latijn voor levende kracht) is een achterhaalde wetenschappelijke theorie die kan beschouwd worden als voorloper van de wet van behoud van energie1. Ze gaf voor het eerst een beschrijving van de kinetische energie2, waarbij de levende kracht verwijst naar alle kinetische energie in een geïsoleerd systeem3.
Vandaag de dag is vis viva opgenomen en vervangen door de moderne theorie van energie. In de sterrenkunde leeft de naam echter nog voort in de vis-vivavergelijking: volgens de klassieke (Newtoniaanse) hemelmechanica draaien satellieten in een ellipsvormige baan rond de Aarde.
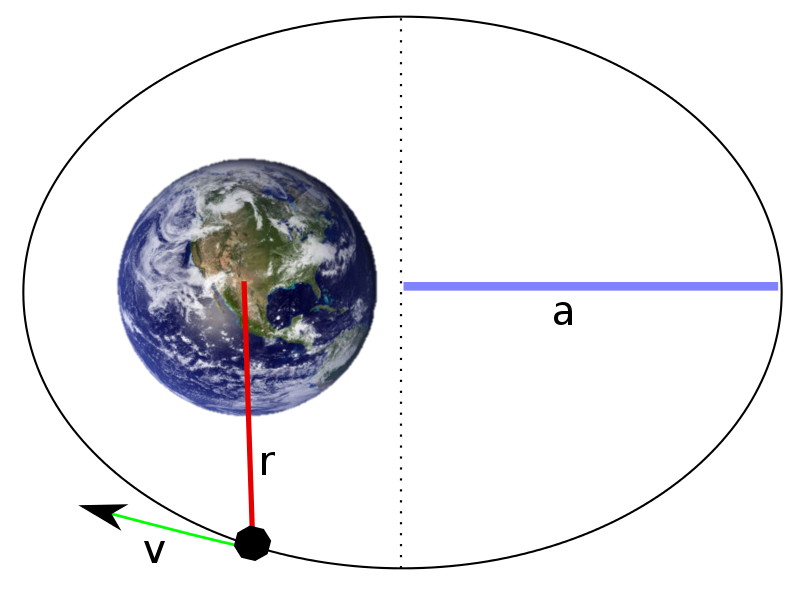
De vis-vivavergelijking legt een verband tussen de grote as $$a$$ van de ellipsvormige baan, de afstand $$r$$ van de satelliet tot het middelpunt van de Aarde en de snelheid $$v$$ van de satelliet ten opzichte van de Aarde: \[ v^2 = \mu \left( \frac{2}{r} - \frac{1}{a} \right) \] De constante $$\mu$$ is de geocentrische gravitatieconstante4. Een benadering van deze constante kan berekend worden als het product van de gravitatieconstante5 $$G$$ en de massa $$M$$ van de Aarde uitgedrukt in kilogram: \[ \mu = G \cdot M \] Er bestaan echter alternatieve methoden om de waarde van $$\mu$$ nauwkeuriger te meten. In deze opgave gebruiken we de volgende nauwkeurige meetwaarde: \[ \mu = 398600{,}4418 \cdot 10^9\,m^3s^{-2}\] Als de lengte van de grote as $$a$$ van een elliptische baan gekend is dan kan daarmee de periode $$p$$ van de satelliet bepaald worden (uitgedrukt in seconden): \[ p = 2\pi \sqrt{\frac{a^3}{\mu}}\] De periode $$p$$ is de tijd die de satelliet nodig heeft om één omwenteling rond de Aarde te maken.
Invoer
Twee reële getallen die elk op een afzonderlijke regel staan:
-
de afstand $$r$$ tussen een satelliet en het middelpunt van de Aarde (uitgedrukt in meter)
-
de snelheid $$v$$ van de satelliet ten opzichte van de Aarde (uitgedrukt in meter/seconde)
Uitvoer
Met deze gegevens kan de lengte $$a$$ (in meter) berekend worden van de grote as van de elliptische baan waarin de satelliet rond de Aarde draait. Hiervoor kan de vis-vivavergelijking herschreven worden als: \[ a = \frac{\mu r}{2\mu - r v^2} \] De periode $$p$$ van de satelliet (uitgedrukt in seconden) wordt dan bekomen als \[ 2\pi \sqrt{\frac{a^3}{\mu}} \]
Er moeten drie regels uitgeschreven worden:
-
de lengte van de grote as $$a$$, uitgedrukt in meter
-
de lengte van de periode $$p$$, uitgedrukt in seconden
-
de lengte van de periode $$p$$, uitgedrukt in een geheel aantal dagen $$d$$, uren $$u$$ en minuten $$m$$ die volledig binnen de periode passen; hierbij moet gelden dat $$0 \leq u < 24$$ en dat $$0 \leq m < 60$$
Bekijk onderstaande voorbeelden om te achterhalen hoe de uitvoer precies moet uitgeschreven worden.
Voorbeeld
Satelliet: het internationaal ruimtestation ISS6
Invoer:
6792000
7658Uitvoer:
grote as: 6787166.808499204 meter
periode: 5564.7257424392155 seconden
periode: 0 dagen, 1 uren en 32 minutenVoorbeeld
Satelliet: ASTRA 1L7, een geostationaire satelliet die onder andere BVN8 uitzendt
Invoer:
35785400
3580.9Uitvoer:
grote as: 42160215.133579694 meter
periode: 86151.96905571753 seconden
periode: 0 dagen, 23 uren en 55 minutenVoorbeeld
Satelliet: PROBA-29
Invoer:
7104000
7485Uitvoer:
grote as: 7093371.63898765 meter
periode: 5945.52283951033 seconden
periode: 0 dagen, 1 uren en 39 minutenVoorbeeld
Satelliet: de Maan10
Invoer:
400000000
977.75Uitvoer:
grote as: 384375790.60599077 meter
periode: 2371619.541180138 seconden
periode: 27 dagen, 10 uren en 46 minuten