Een driehoek is een meetkundige figuur die ontstaat door drie punten die niet op een rechte lijn liggen met elkaar te verbinden. De verbindende lijnstukken worden de zijden van de driehoek genoemd. De hoeken tussen de zijden aan de binnenkant van een driehoek worden de binnenhoeken van de driehoek genoemd.

Driehoeken kunnen ingedeeld worden op basis van de lengtes van hun zijden:

• gelijkzijdige driehoek: alle zijden zijn even lang

• gelijkbenige driehoek: minstens twee zijden zijn even lang

• ongelijkzijdige driehoek: alle zijden hebben een verschillende lengte

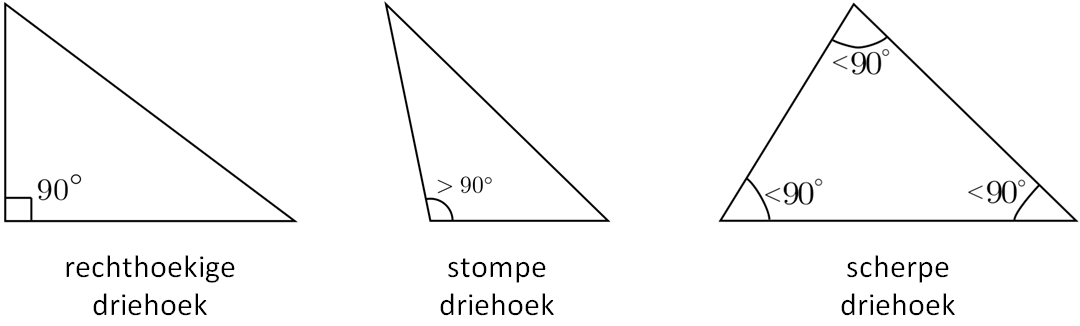
Driehoeken kunnen ook ingedeeld worden op basis van hun binnenhoeken:

• scherpe driehoek: alle hoeken zijn kleiner dan 90°

• rechthoekige driehoek: één van de hoeken is gelijk aan 90°

• stompe driehoek: één van de hoeken is groter dan 90°

Lengte van zijde tussen twee punten

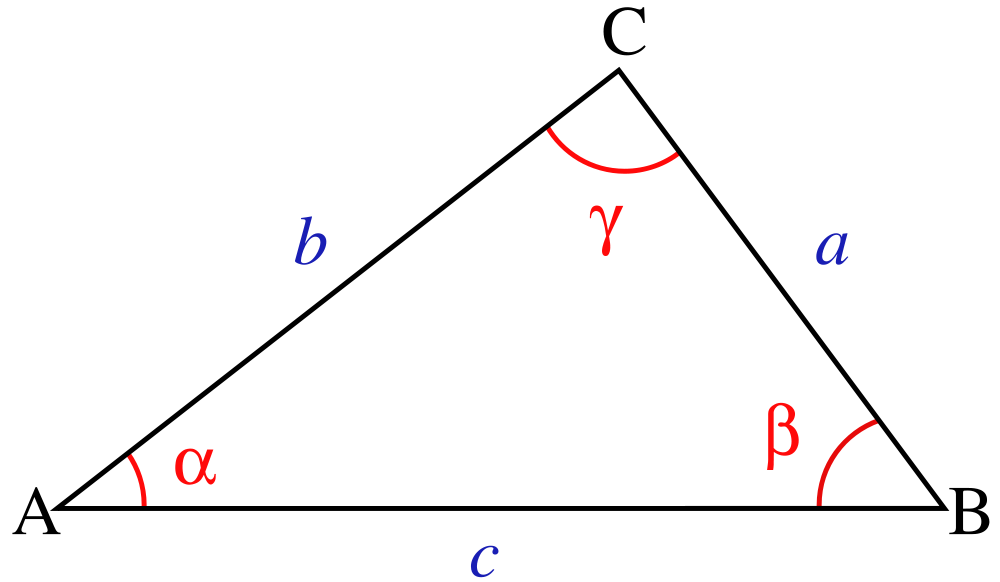
De lengte $$l$$ van een zijde die de hoekpunten $$(x_1, y_1)$$ en $$(x_2, y_2)$$ verbindt, kan berekend worden als \[ l = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \]

Binnenhoek gevormd door twee zijden

De grootte van de binnenhoek $$\gamma$$ gevormd door twee zijden van een driehoek kan berekend worden op basis van de cosinusregel \[cos(\gamma) = \frac{a^2+b^2-c^2}{2ab}\] Hierbij zijn $$a$$ en $$b$$ de lengten van de zijden die de binnenhoek $$\gamma$$ vormen, en is $$c$$ de lengte van de zijde die tegenover de binnenhoek $$\gamma$$ staat.

Vergelijken van floating point getallen

Bij deze opgave moet je de lengte van zijden en de grootte van hoeken vergelijken. Let daarbij op het feit dat deze waarden voorgesteld worden als floating point getallen, waarbij kleine afrondingsfouten optreden als ze voorgesteld worden in een computergeheugen. Het kan dus voorvallen dat een variabele hoek die een hoek van 90° voorstelt, eigenlijk als waarde 90.00000001 heeft. Daardoor is het geen goed idee om op de volgende manier te testen of dit een rechte hoek voorstelt:

if hoek == 90:
    print('rechte hoek')

In plaats daarvan kan de voorwaarde geherformuleerd worden door te stellen dat de grootte van de hoek "dicht genoeg" bij 90° moet liggen. In het volgende codefragment stellen we bijvoorbeeld dat de hoek niet meer dan 0.000001 mag afwijken van 90°:

if abs(hoek - 90) < 1e-6:
    print('rechte hoek')

Bekijk deze video¹ waarin extra uitleg wordt gegeven bij het werken met floating point getallen.

Opgave

Bepaal de indeling van de driehoek die gevormd wordt door drie gegeven punten die niet op een rechte lijn liggen, zowel op basis van de zijden als op basis van de binnenhoeken.

Invoer

Zes reële getallen, elk op een afzonderlijke regel. Elk paar opeenvolgende getallen stelt de $$(x, y)$$-coördinaat voor van een hoekpunt van een driehoek. Je mag ervan uitgaan dat deze hoekpunten niet op eenzelfde lijn liggen.

Uitvoer

Een omschrijving van de indeling van de driehoek die gevormd wordt door de drie punten waarvan de coördinaten in de invoer gegeven worden. Gebruik voor de omschrijving de template Driehoek classificatie: indeling_zijden indeling_hoeken, waarbij indeling_zijden de term is die de indeling van de driehoek op basis van de zijden aangeeft en indeling_hoeken de term is die de indeling van de driehoek op basis van de hoeken aangeeft. Gebruik telkens de meest specifieke term die van toepassing is op de driehoek.

Voorbeeld

Invoer:

-5.018651714882998
5.273815977515895
-4.1327268984230505
5.7376448463677665
-4.596555767274922
6.623569662827715

Uitvoer:

Driehoek classificatie: rechthoekige driehoek