Een self-avoiding walk¹ (SAW) bestaat uit een reeks stappen op een rechthoekig rooster, waarbij hetzelfde punt hoogstens één keer bezocht wordt. SAWs werden geïntroduceerd door de chemicus Paul Flory voor het modelleren van het gedrag van ketenachtige structuren zoals solventen en polymeren. De ruimtelijke invulling van dergelijk structuren laat immers niet toe dat hetzelfde punt meerdere keren bezet wordt. Het is extreem moeilijk om de eigenschappen van SAWs op een wiskundige manier af te leiden. Desondanks hebben chemici en natuurkundigen reeds verschillende wetmatigheden van macromoleculen afgeleid, waarbij het vermoeden van hun geldigheid berust op numerieke simulaties. Het leverde Flory in 1974 uiteindelijk ook de Nobelprijs in de scheikunde² op.

Om numerieke simulaties te kunnen uitvoeren, stellen we een polymeer in het cartesisch vlak voor als een reeks monomeren die aaneengeschakeld worden volgens het principe van een self-avoiding walk. We veronderstellen daarbij dat het eerste monomeer in de oorsprong $$(0,0)$$ van het vlak ligt, en dat de $$x$$-as van het coördinatenstelsel naar rechts gericht is, en de $$y$$-as naar boven. Het volgende monomeer uit de reeks ligt telkens één eenheidsstap boven, onder, links of rechts van het vorige monomeer $$(x,y)$$, zoals geïllustreerd in onderstaande figuur.

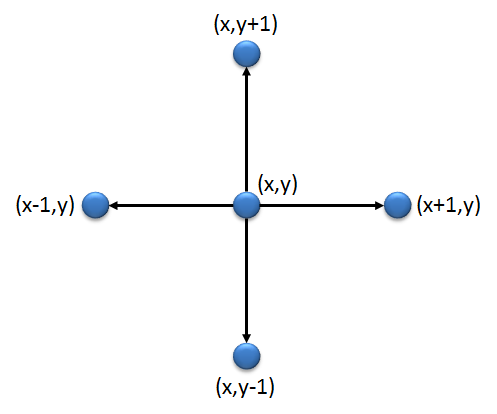
Als we een positie in het cartesisch vlak voorstellen als een tuple met twee elementen $$(x,y)$$, dan kunnen we een polymeer voorstellen als een lijst van tuples, waarbij het eerste tuple de oorsprong $$(0,0)$$ voorstelt.

Opgave

1. Schrijf een functie groei die voor een monomeer op een gegeven positie $$(x,y)$$ (waarbij $$x, y \in \mathbb{Z}$$), een positie voor het volgende monomeer in een polymeer bepaalt. Deze positie moet willekeurig gekozen worden uit de mogelijke posities boven, onder, links en rechts van het vorige monomeer. Posities die reeds door monomeren van het polymeer zijn ingenomen mogen hierbij niet opnieuw gekozen worden. Aan de functie moeten verplicht twee argumenten doorgegeven worden. Het eerste argument is een tuple met twee elementen dat de positie $$(x,y)$$ van het vorige monomeer aangeeft. Het tweede argument is een collectieobject dat alle posities (opnieuw wordt elke positie voorgesteld als een tuple van twee gehele getallen) bevat die reeds door monomeren van het polymeer zijn ingenomen. Als resultaat moet de functie één van de mogelijke posities (opnieuw voorgesteld door een tuple van twee elementen) teruggeven die rondom de gegeven positie ligt en die nog niet bezet is door een monomeer van het polymeer. Indien alle vier de posities rondom de gegeven positie reeds bezet zijn, dan moet de functie de waarde None als resultaat teruggeven.

2. Schrijf een functie polymeer die een lijst van tuples met twee elementen als resultaat teruggeeft. Deze lijst stelt een polymeer voor, waarbij de tuples de posities van de verschillende monomeren van het polymeer voorstellen. Het eerste element van de lijst is het tuple $$(0,0)$$ dat de oorsprong van het cartesisch vlak voorstelt. Gebruik de functie groei om op basis van een vorige positie, telkens een volgende positie voor een monomeer achteraan de lijst toe te voegen. Blijf deze procedure herhalen totdat alle vier de posities rondom de laatste positie bezet zijn en het polymeer dus niet verder kan uitgebreid worden.

Voorbeeld

>>> groei((0, 0), [(1, 0), (-1, 0), (0, -1)])
(0, 1)
>>> groei((0, 0), [(1, 0), (-1, 0), (0, 1)])
(0, -1)
>>> groei((0, 0), [(1, 0), (0, 1), (0, -1)])
(-1, 0)
>>> groei((0, 0), [(-1, 0), (0, 1), (0, -1)])
(1, 0)
>>> groei((0, 0), [(1, 0), (-1, 0), (0, 1), (0, -1)])

>>> polymeer()
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2), (0, 1), (1, 1)]
>>> polymeer()
[(0, 0), (1, 0), (2, 0), (2, -1), (3, -1), (4, -1), (4, 0), (4, 1), (3, 1), (3, 0)]