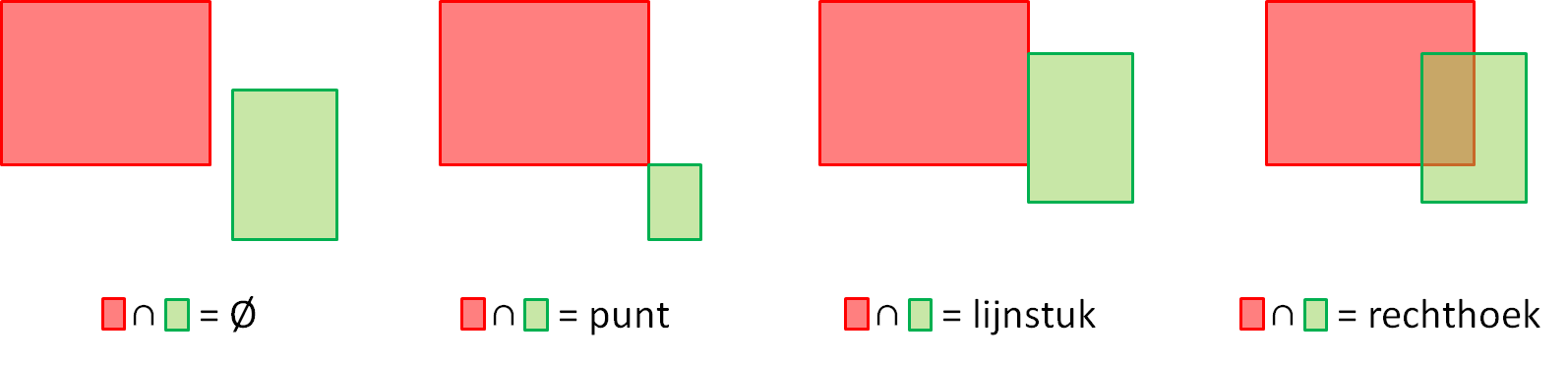
Als we de doorsnede van twee gegeven rechthoeken in het Euclidische vlak moeten bepalen, dan zijn er vier mogelijkheden. De doorsnede is ofwel leeg, een punt (gemeenschappelijk hoekpunt), een lijnstuk of een rechthoek.

Opgave

Definieer een klasse Punt waarmee punten in het Euclidische vlak met gehele coördinaten kunnen voorgesteld worden. Deze klasse moet ondersteuning bieden aan de volgende methoden:

• Een initialisatiemethode __init__ die toelaat om een punt in het Euclidische vlak aan te maken op basis van een $$x$$- en $$y$$-coördinaat. Beide coördinaten kunnen optioneel als de parameters x en y aan de initialisatiemethode doorgegeven worden ($$x, y \in \mathbb{Z}$$), en hebben de waarde nul indien ze niet worden opgegeven. De initialisatiemethode moet de opgegeven waarden of hun standaardwaarden respectievelijk toekennen aan de attributen x en y van het nieuw aangemaakte object.

• Methoden __str__ en __repr__ die beide een stringvoorstelling van een punt teruggeven onder de vorm "Punt(x, y)", waarbij x en y respectievelijk de $$x$$- en $$y$$-coördinaat van het punt in het Euclidische vlak voorstellen.

• Methoden __lt__, __le__, __eq__, __ne__, __gt__ en __ge__ die toelaten om twee punten uit het Euclidische vlak onderling te vergelijken aan de hand van de Python operatoren <, <=, ==, !=, > en >=. De vergelijking van twee punten gebeurt door eerst hun $$x$$-coördinaten te vergelijken, en daarna ook de $$y$$-coördinaten als de $$x$$-coördinaten gelijk zijn.

• Een methode afstand die kan gebruikt worden om de Euclidische afstand tussen twee punten in het Euclidische vlak te berekenen. De Euclidische afstand tussen twee punten $$(x_1, y_1)$$ en $$(x_2, y_2)$$ wordt gegeven door \[ \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \]

Definieer een klasse Lijnstuk waarmee lijnstukken in het Euclidische vlak kunnen voorgesteld worden die een lengte hebben groter dan nul. Deze klasse moet ondersteuning bieden aan de volgende methoden:

• Een initialisatiemethode __init__ die toelaat om een lijnstuk in het Euclidische vlak aan te maken op basis twee gegeven punten. Aan deze initialisatiemethode moeten twee objecten van de klasse Punt doorgegeven worden, die beide uiteinden van het lijnstuk voorstellen. Het kleinste van deze punten moet door de initialisatiemethode toegekend worden aan het attribuut punt1 van het nieuw aangemaakte object, en het grootste punt aan het attribuut punt2. Bekijk onderstaand voorbeeld om na te gaan welke actie de initialisatiemethode moet nemen indien het opgegeven lijnstuk lengte nul heeft.

• Methoden __str__ en __repr__ die beide een stringvoorstelling van het lijnstuk teruggeven onder de vorm "Lijnstuk(Punt(x1, y1), Punt(x2, y2))", waarbij x1 en y1 respectievelijk de $$x$$- en $$y$$-coördinaat van het kleinste eindpunt van het lijnstuk voorstellen en x2 en y2 respectievelijk de $$x$$- en $$y$$-coördinaat van het grootste eindpunt van het lijnstuk.

• Een methode lengte die kan gebruikt worden om de lengte van het lijnstuk te bepalen. De lengte van een lijnstuk wordt berekend als de Euclidische afstand tussen de twee eindpunten van het lijnstuk.

Definieer een klasse Rechthoek waarmee rechthoeken in het Euclidische vlak kunnen voorgesteld worden die een oppervlakte hebben groter dan nul. Deze klasse moet ondersteuning bieden aan de volgende methoden:

• Een initialisatiemethode __init__ die toelaat om een rechthoek in het Euclidische vlak aan te maken op basis twee gegeven hoekpunten die diametraal tegenover elkaar liggen. Aan deze initialisatiemethode moeten twee objecten van de klasse Punt doorgegeven worden, die diametraal tegenover elkaar liggende hoekpunten van de rechthoek voorstellen. De initialisatiemethode moet aan de attributen punt1 en punt2 van het nieuw aangemaakte object respectievelijk het hoekpunt in de linkeronderhoek en de rechterbovenhoek van de rechthoek toekennen. Bekijk onderstaand voorbeeld om na te gaan welke actie de initialisatiemethode moet nemen indien de opgegeven rechthoek oppervlakte nul heeft.

• Methoden __str__ en __repr__ die beide een stringvoorstelling van de rechthoek teruggeven onder de vorm "Rechthoek(Punt(x1, y1), Punt(x2, y2))", waarbij x1 en y1 respectievelijk de $$x$$- en $$y$$-coördinaat van het hoekpunt in de linkeronderhoek van de rechthoek voorstellen en x2 en y2 respectievelijk de $$x$$- en $$y$$-coördinaat van het hoekpunt in de rechterbovenhoek van de rechthoek.

• Een methode oppervlakte die kan gebruikt worden om de oppervlakte van de rechthoek te bepalen. De oppervlakte van een rechthoek wordt berekend als het product van de breedte en de hoogte van de rechthoek.

• Een methode doorsnede die kan gebruikt worden om de doorsnede van twee rechthoeken te bepalen. Deze methode moet de waarde None teruggeven indien de twee rechthoeken elkaar niet overlappen, of een object van de klasse Punt, Lijnstuk of Rechthoek dat de overlap van de twee rechthoeken omschrijft als een gemeenschappelijk hoekpunt, een gemeenschappelijke zijde of een gemeenschappelijke rechthoek.

Voorbeeld

>>> p1 = Punt(1, 2)
>>> p1
Punt(1, 2)
>>> print(p1.x, p1.y)
1 2
>>> p2 = Punt(3, 5)
>>> print(p2)
Punt(3, 5)
>>> p1 < p2
True
>>> p1.afstand(p2)
3.605551275463989

>>> l1 = Lijnstuk(Punt(1,2), Punt(3, 4))
>>> l1
Lijnstuk(Punt(1, 2), Punt(3, 4))
>>> print(l1.punt1, l1.punt2)
Punt(1, 2) Punt(3, 4)
>>> l1.lengte()
2.8284271247461903
>>> l2 = Lijnstuk(Punt(5, -4), Punt(-2, 3))
>>> print(l2)
Lijnstuk(Punt(-2, 3), Punt(5, -4))
>>> l2.lengte()
9.899494936611665
>>> l3 = Lijnstuk(Punt(1,2), Punt(1, 2))
Traceback (most recent call last):
AssertionError: lijnstuk moet lengte hebben die groter is dan nul

>>> r1 = Rechthoek(Punt(1, 1), Punt(4, 4))
>>> r1
Rechthoek(Punt(1, 1), Punt(4, 4))
>>> r1.oppervlakte()
9
>>> r2 = Rechthoek(Punt(6, 3), Punt(3, 6))
>>> r3 = Rechthoek(Punt(6, 3), Punt(4, 2))
>>> print(r3)
Rechthoek(Punt(4, 2), Punt(6, 3))
>>> r3.oppervlakte()
2
>>> r4 = Rechthoek(Punt(-7, -3), Punt(1, 1))
>>> r1.doorsnede(r2)
Rechthoek(Punt(3, 3), Punt(4, 4))
>>> r1.doorsnede(r3)
Lijnstuk(Punt(4, 2), Punt(4, 3))
>>> r2.doorsnede(r3)
Lijnstuk(Punt(4, 3), Punt(6, 3))
>>> r1.doorsnede(r4)
Punt(1, 1)
>>> r5 = Rechthoek(Punt(1, 1), Punt(1, 1))
Traceback (most recent call last):
AssertionError: rechthoek moet oppervlakte hebben die groter is dan nul