p_load(AUC, caret)
Labels
We transform the labels to 0 and 1. Note that the dependent variable is -1 and +1, compared to 0 and 1 otherwise. In general, it does not matter whether you use one or the other since the performance will stay the same. However, in computer science -1 and +1 are preferred and in statistics 0 and 1.
y_train <- as.factor(ifelse(train$label==-1, 0,1))
y_test <- as.factor(ifelse(test$label==-1, 0,1))
Logistic regression
We will apply logistic regression.
LR <- glm(y_train ~., data = as.data.frame(trainer$v),family = "binomial")
LR
Call: glm(formula = y_train ~ ., family = "binomial", data = as.data.frame(trainer$v))
Coefficients:
(Intercept) V1 V2 V3 V4 V5 V6 V7 V8 V9
-1.353e+15 6.847e+15 6.362e+14 -1.074e+16 2.642e+15 1.946e+15 7.665e+15 -3.235e+15 -4.093e+15 -5.874e+15
V10 V11 V12 V13 V14 V15 V16 V17 V18 V19
-2.202e+15 2.476e+15 -7.263e+14 5.029e+15 3.680e+15 -1.781e+15 -3.525e+15 -2.638e+15 3.892e+15 -1.205e+15
V20
-1.156e+15
Degrees of Freedom: 56 Total (i.e. Null); 36 Residual
Null Deviance: 78.58
Residual Deviance: 1081 AIC: 1123
preds <- predict(LR,tester,type = "response")
AUC
Next, we can calculate the AUC and plot the ROC curve with the AUC package.
AUC::auc(roc(preds,y_test))
[1] 0.6577381
ROC curve
plot(roc(preds,y_test))
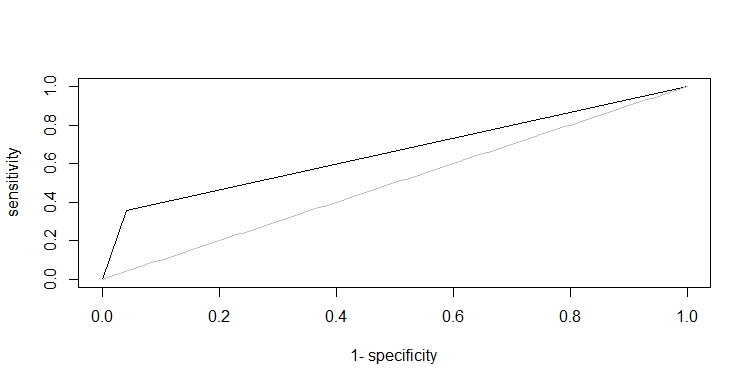
Performance can be better, but if you use more advanced methods (e.g., random forest) or perform regularization (e.g., LASSO), you will already improve the performance. Normally you should use cross-validation to see whether your results are robust. If performance is satisfactory, so you can use this model to extrapolate to unseen results. Sometimes other performance measures are also reported (accuracy). To do so, let’s just use a 0.5 cut-off. Since logistic regression uses the sigmoid function, probabilities are well-calibrated.
preds_lab <- ifelse(preds > 0.5,1,0)
Confusion matrix
xtab <- table(preds_lab, y_test)
confusionMatrix(xtab)
Confusion Matrix and Statistics
y_test
preds_lab 0 1
0 23 9
1 1 5
Accuracy : 0.7368
95% CI : (0.569, 0.866)
No Information Rate : 0.6316
P-Value [Acc > NIR] : 0.11814
Kappa : 0.3581
Mcnemar's Test P-Value : 0.02686
Sensitivity : 0.9583
Specificity : 0.3571
Pos Pred Value : 0.7188
Neg Pred Value : 0.8333
Prevalence : 0.6316
Detection Rate : 0.6053
Detection Prevalence : 0.8421
Balanced Accuracy : 0.6577
'Positive' Class : 0
From the confusion matrix, we can conclude that the results are good in terms of accuracy. However, we see that we are better in detecting positive comments (sensitivity) than in detecting negative comments (specificity).
Exercise
Apply logistic regression to the oxfam data, compute the AUC value and save
it as auc_oxfam.
To download the SentimentReal dataset click
here1.
To download the oxfam dataset click
here2.
Assume that:
- The variables
train_oxfam,test_oxfam,trainer, andtrainer, that were calculated in the previous exercise, are given.