De zeef van Eratosthenes is een methode om alle priemgetallen te vinden tussen 1 en een gegeven getal. Eratosthenes¹ was een Griekse wiskundige werkzaam aan de bibliotheek van Alexandrië.

De methode werkt als volgt. Je begint met een lijst te maken die bestaat uit de getallen 1 tot en met een zeker “hoogste getal.”

• Begin met zoeken vanaf 2, omdat 1 geen priemgetal is.
• Schrap alle veelvouden van 2. Die kunnen al zeker niet priem zijn, want ze zijn deelbaar door 2.
• Zoek het volgende, niet geschrapte, getal op. In dit geval is dat 3.
• Schrap alle veelvouden van 3. Die kunnen zeker niet priem zijn, want ze zijn deelbaar door 3.
• Zoek het volgende, niet geschrapte, getal op. In dit geval is dat 5.
• enz…

De getallen die uiteindelijk overblijven zijn de priemgetallen.

Hieronder zie je de methode uitgevoerd op een lijst met getallen tot 120.

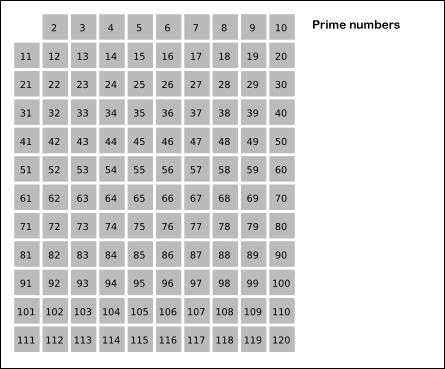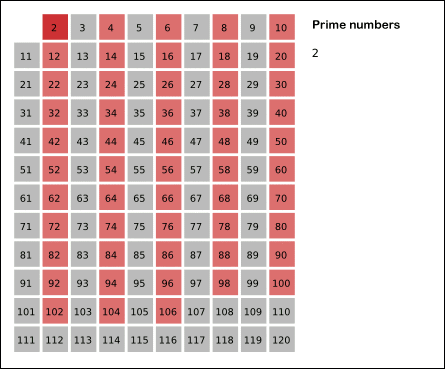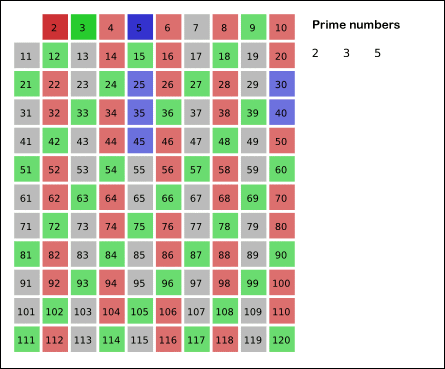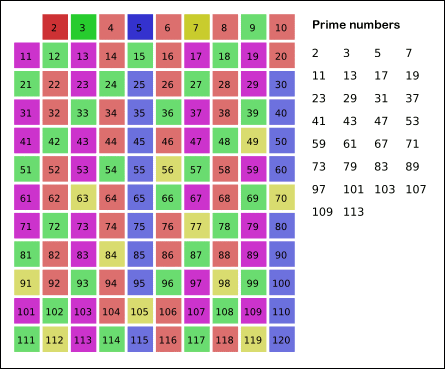
Opgave

Schrijf zelf een functie zeef_eratosthenes( max ) dat de priemgetallen kleiner dan of gelijk aan een bepaalde maximale waarde uitzeeft.

• Gebruik een lijst van 1 tot en met het maximale getal in Python.
• Zet de waarde van 1 op nul, omdat 1 geen priemgetal is.
• Gebruik vervolgens een herhaling. Zoek naar het eerste nummer dat niet op 0 staat, wat nummer 2 is. Dat betekent dat 2 een priemgetal is, maar alle veelvouden van 2 zijn dat niet. Dus zet alle veelvouden van 2 op 0. Zoek dan naar het volgende nummer dat geen nul is, en dat is 3. Zet alle veelvouden van 3 op nul. Zoek dan naar het volgende nummer dat geen nul is, en dat is 5. Zet alle veelvouden van 5 op nul. Verwerk zo de hele list…
• Als je klaar bent, zijn alleen nog de getallen over die priemgetallen zijn. Gebruik deze methode om alle priemgetallen tussen 1 en 100 te bepalen.

Voorbeelden

>>> zeef_eratosthenes( 50 )
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

>>> zeef_eratosthenes( 100 )
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]