In de tumultueus verlopen Amerikaanse presidentsverkiezingen van 1876 stuurde het campagneteam van de democraat Samuel J. Tilden heel wat gecodeerde berichten naar haar tussenpersonen in de verschillende strijdstaten.

In de Amerikaanse presidentsverkiezingen van 1876 nam de democraat Samuel J. Tilden (links) het op tegen de republikein Rutherford B. Hayes (rechts). De kiesstrijd verliep bijzonder bitsig en werd uiteindelijk gewonnen door Hayes, die zo de 19e president van de Verenigde Staten werd van 1877 tot 1881.

Twee jaar na de verkiezingen publiceerde de New York Daily Tribune ontcijferde versies van enkele van deze telegrammen. Hieruit kon opgemaakt worden dat Tilden's campagneteam geprobeerd had om de verkiezingen te winnen door sommige verkiezingsbeambten om te kopen. Hier is één van die telegrammen:

Gecodeerd telegram dat verstuurd werd door het campagneteam van Samuel Tilden.

Omdat er in het gecodeerde bericht maar 10 verschillende letters gebruikt worden, is het waarschijnlijk dat de code gebruik maakt van letterparen (bigrammen). Als we nu elk van de opeenvolgende letterparen uit het bericht afbeelden op een verschillende letter van het alfabet

Afbeelding van opeenvolgende letterparen op verschillende letters van het alfabet.

dan wordt het het gecodeerde bericht een cryptogram dat eenvoudig kan ontcijferd worden.

Ontcijferde versie van een telegram dat verstuurd werd door het campagneteam van Samuel Tilden.

Het campagneteam van Tilden deed hetzelfde met cijferparen. Zo bleek het telegram

Gecodeerde telegram dat verstuurd werd door het campagneteam van Samuel Tilden.

bijvoorbeeld een gecodeerde versie te zijn van het bericht

Ontcijferde versie van een telegram dat verstuurd werd door het campagneteam van Samuel Tilden.

In 1879 achterhaalden experten van de Tribune met welke letter- en cijferparen elk van de letters van het alfabet correspondeerden:

Volledige afbeelding van bigrammen van letters en cijfers op de verschillende letters van het alfabet.

Maar het was pas in 1952 dat cryptograaf William F. Friedman de oorspronkelijke tabel reconstrueerde die de tussenpersonen gebruikt hadden om de codeersleutel te kunnen onthouden:

Pas in 1952 reconstrueerde de cryptograaf William F. Friedman deze tabel die de tussenpersonen gebruikt hadden om de codeersleutel te kunnen onthouden.

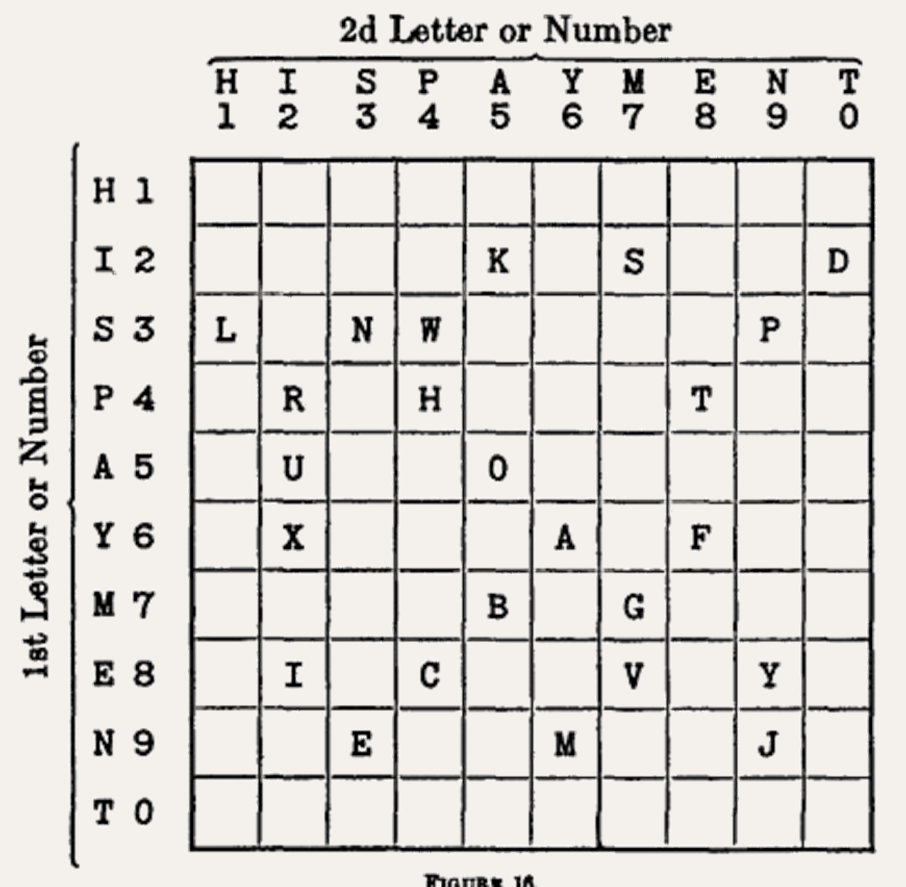
In zijn boek Secret Ciphers of the 1876 Presidential Election schreef Beaird Glover hierover:

"It is amusing to note that the conspirators selected as their key a phrase quite in keeping with their attempted illegalities — HIS PAYMENT — for bribery seems to have played a considerable part in that campaign."

Opgave

Codeer en decodeer berichten door gebruik te maken van codeersleutels zoals deze die gebruikt werden door het campagneteam van Tilden. Hierbij worden alle letters van een bericht gecodeerd naar bigrammen die bestaan uit twee hoofdletters. Bij het coderen van een bericht wordt geen onderscheid gemaakt tussen hoofdletters en kleine letters, en worden alle karakters die geen letter zijn genegeerd.

Een codeersleutel bestaat uit twee onderdelen. Het eerste onderdeel is een sleutelwoord dat bestaat uit verschillende hoofdletters die gebruikt worden om de rijen en kolommen van een vierkant rooster te markeren. In onderstaand voorbeeld gebruiken we hiervoor het sleutelwoord ABCD om de rijen (van boven naar onder) en de kolommen (van links naar rechts) te markeren.

Voorbeeld van een tabel die gebruikt wordt voor het coderen en decoderen van berichten.

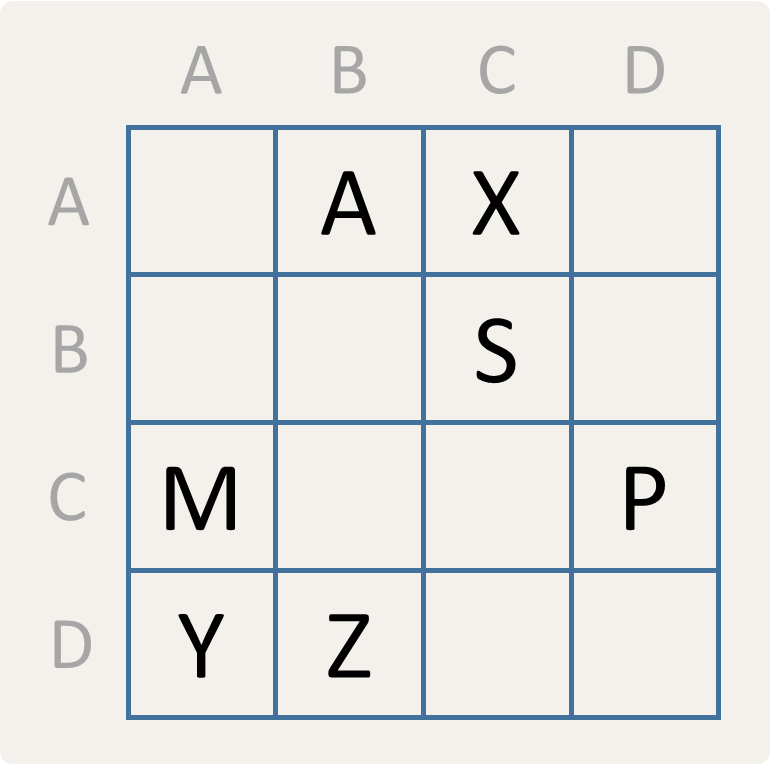
Het tweede onderdeel is een omschrijving die aangeeft hoe een aantal verschillende letters van het alfabet in het rooster moeten ingevuld worden. Zo een omschrijving bestaat alternerend uit reeksen opeenvolgende hoofdletters en getallen (die uit meerdere cijfers kunnen bestaan), en kan zowel met een hoofdletter als met een getal beginnen. Deze omschrijving wordt gebruikt om het rooster in te vullen met de hoofdletters uit de omschrijving. We beginnen hierbij in de cel linksboven. Een hoofdletter geeft aan dat die letter in de huidige cel moet ingevuld worden. Een getal geeft aan dat het overeenkomstig aantal cellen moet overgeslaan worden als we het rooster van links naar rechts en van boven naar onder doorlopen. Zo komt de plaatsing van de letters in bovenstaand voorbeeldrooster overeen met de omschrijving 1AX3S1M2PYZ. Merk op dat we na de laatste Z in de omschrijving ook nog het getal 2 mogen zetten om aan te geven dat de laatste twee cellen van het rooster leeg zijn, maar dat is optioneel.

Definieer een klasse Codeersleutel die codeersleutels voorstelt waarmee berichten kunnen gecodeerd en gedecodeerd worden. Bij het aanmaken van een nieuwe codeersleutel (Codeersleutel) moeten een sleutelwoord (str) en een omschrijving (str) doorgegeven worden die de codeersleutel vastleggen. Hierbij mag de klasse ervan uitgaan dat zowel het sleutelwoord als de omschrijving geldig zijn, zonder dat dit expliciet moet gecontroleerd worden. Een codeersleutel $$c$$ (Codeersleutel) is onveranderlijk (immutable) en moet minstens de volgende eigenschappen hebben:

Een eigenschap rooster die het vierkant rooster voorstelt dat gebruikt wordt door codeersleutel $$c$$. Dit rooster wordt voorgesteld als een lijst (list) met de rijen van het rooster (van boven naar onder), waarbij elke rij zelf voorgesteld wordt als een lijst (list) van karakters (str; van links naar rechts). De elementen van elke rij bestaan uit de hoofdletters uit de corresponderende cellen van het rooster, of een koppelteken (-) als een cel geen hoofdletter bevat.
Een eigenschap afbeelding die verwijst naar een dictionary (dict) die elke letter (str) uit het rooster dat gebruikt wordt door codeersleutel $$c$$ afbeeldt op het bigram (str) dat bestaat uit de samenstelling van de twee letters die respectievelijk de rij en de kolom markeren waarop de letter terug te vinden is in het rooster.

Voorts moet codeersleutel $$c$$ (Codeersleutel) minstens de volgende methoden ondersteunen:

Een methode codeer waaraan een bericht (str) moet doorgegeven worden. De methode moet het gecodeerde bericht (str; in hoofdletters) teruggeven dat verkregen wordt op basis van codeersleutel $$c$$. Bij het coderen wordt enkel rekening gehouden met de letters uit het gegeven bericht (alle karakters die geen letter zijn moeten dus genegeerd worden), en mag geen onderscheid gemaakt worden tussen hoofdletters en kleine letters. Als het gegeven bericht niet kan gecodeerd worden met codeersleutel $$c$$, dan moet een AssertionError opgeworpen worden met de boodschap ongeldig bericht.
Een methode decodeer waaraan een bericht (str) moet doorgegeven worden dat gecodeerd werd met codeersleutel $$c$$ (cfr. methode codeer). De methode moet de letters van het originele bericht (str; in hoofdletters) teruggeven. Als het gegeven bericht niet kan gedecodeerd worden met codeersleutel $$c$$, dan moet een AssertionError opgeworpen worden met de boodschap ongeldig bericht.

Voorbeeld

        >>> sleutel = Codeersleutel('ABCD', '1AX3S1M2PYZ')
>>> sleutel.rooster
[['-', 'A', 'X', '-'], ['-', '-', 'S', '-'], ['M', '-', '-', 'P'], ['Y', 'Z', '-', '-']]
>>> sleutel.afbeelding
{'A': 'AB', 'X': 'AC', 'S': 'BC', 'M': 'CA', 'P': 'CD', 'Y': 'DA', 'Z': 'DB'}
>>> sleutel.codeer('spam')
'BCCDABCA'
>>> sleutel.decodeer('BCCDABCA')
'SPAM'
>>> sleutel.codeer('eggs')
Traceback (most recent call last):
AssertionError: ongeldig bericht
>>> sleutel.decodeer('BCCDBACA')
Traceback (most recent call last):
AssertionError: ongeldig bericht

>>> sleutel02 = Codeersleutel('HISPAYMENT', '14K1S2DL1NW4P2R1H3T3U2O6X3A1F6B1G4I1C2V1Y3E2M2J')
>>> sleutel02.rooster
[['-', '-', '-', '-', '-', '-', '-', '-', '-', '-'], ['-', '-', '-', '-', 'K', '-', 'S', '-', '-', 'D'], ['L', '-', 'N', 'W', '-', '-', '-', '-', 'P', '-'], ['-', 'R', '-', 'H', '-', '-', '-', 'T', '-', '-'], ['-', 'U', '-', '-', 'O', '-', '-', '-', '-', '-'], ['-', 'X', '-', '-', '-', 'A', '-', 'F', '-', '-'], ['-', '-', '-', '-', 'B', '-', 'G', '-', '-', '-'], ['-', 'I', '-', 'C', '-', '-', 'V', '-', 'Y', '-'], ['-', '-', 'E', '-', '-', 'M', '-', '-', 'J', '-'], ['-', '-', '-', '-', '-', '-', '-', '-', '-', '-']]
>>> sleutel02.afbeelding
{'K': 'IA', 'S': 'IM', 'D': 'IT', 'L': 'SH', 'N': 'SS', 'W': 'SP', 'P': 'SN', 'R': 'PI', 'H': 'PP', 'T': 'PE', 'U': 'AI', 'O': 'AA', 'X': 'YI', 'A': 'YY', 'F': 'YE', 'B': 'MA', 'G': 'MM', 'I': 'EI', 'C': 'EP', 'V': 'EM', 'Y': 'EN', 'E': 'NS', 'M': 'NY', 'J': 'NN'}
>>> sleutel02.codeer('Have Marble and Coyle telegraph for influential men from Delaware and Virginia.')
'PPYYEMNSNYYYPIMASHNSYYSSITEPAAENSHNSPENSSHNSMMPIYYSNPPYEAAPIEISSYESHAINSSSPEEIYYSHNYNSSSYEPIAANYITNSSHYYSPYYPINSYYSSITEMEIPIMMEISSEIYY'
>>> sleutel02.decodeer('PPYYEMNSNYYYPIMASHNSYYSSITEPAAENSHNSPENSSHNSMMPIYYSNPPYEAAPIEISSYESHAINSSSPEEIYYSHNYNSSSYEPIAANYITNSSHYYSPYYPINSYYSSITEMEIPIMMEISSEIYY')
'HAVEMARBLEANDCOYLETELEGRAPHFORINFLUENTIALMENFROMDELAWAREANDVIRGINIA'
>>> sleutel02.codeer('Indications of weakening here.')
'EISSITEIEPYYPEEIAASSIMAAYESPNSYYIANSSSEISSMMPPNSPINS'
>>> sleutel02.decodeer('EISSITEIEPYYPEEIAASSIMAAYESPNSYYIANSSSEISSMMPPNSPINS')
'INDICATIONSOFWEAKENINGHERE'
>>> sleutel02.codeer('Press advantage and watch Board.')
'SNPINSIMIMYYITEMYYSSPEYYMMNSYYSSITSPYYPEEPPPMAAAYYPIIT'
>>> sleutel02.decodeer('SNPINSIMIMYYITEMYYSSPEYYMMNSYYSSITSPYYPEEPPPMAAAYYPIIT')
'PRESSADVANTAGEANDWATCHBOARD'