Sinds 1998 is curling officieel een olympische wintersport. Aan de vooravond van de Olymische Winterspelen wordt het dus hoog tijd om deze sport — die wat weg heeft van petanque¹ op ijs — wat beter te leren kennen.

In curling schuiven twee teams van vier spelers (team rood en team geel) om beurt zware, gepolijste granieten stenen op een ijsvlak naar het huis: een doelgebied dat onderverdeeld is in vier concentrische ringen. Elk team heeft acht stenen die ze om beurt mogen schuiven. De bedoeling is om tijdens een wedstrijd zoveel mogelijk punten te scoren. Een wedstrijd bestaat meestal uit acht of tien ends, die voltooid worden nadat beide teams al hun stenen gespeeld hebben.

Bij het beëindigen van een end worden punten gescoord voor stenen die het dichtst bij de dolly (het middelpunt van het huis) liggen. Voor elke steen die dichter bij de dolly ligt dan de dichtst bij de dolly liggende steen van de tegenpartij scoort men één punt. Enkel stenen die in het huis liggen, worden in rekening gebracht bij het bepalen van de score. Een steen ligt in het huis als hij — ook al is het maar een fractie — overlapt met de cirkel die gevormd wordt door de buitenste rand van de buitenste ring van het huis. Hieronder zie je enkele voorbeelden van scores bij het beëindigen van een end.

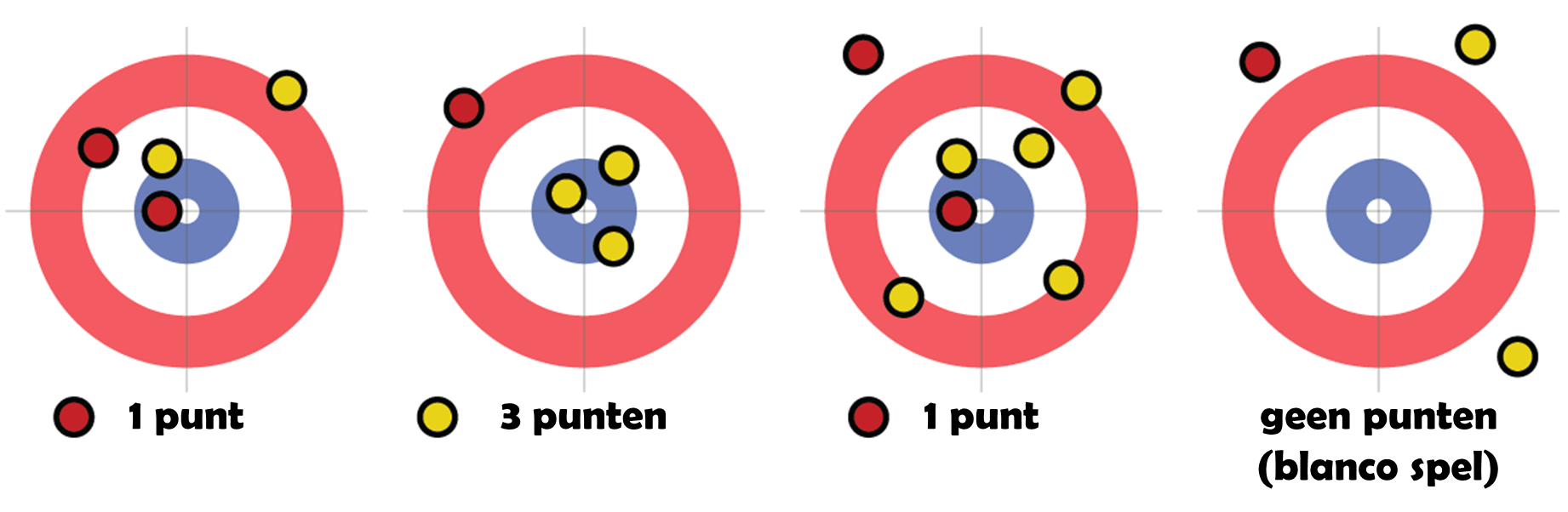
De kleuren van de ringen hebben geen betekenis. Ze worden alleen gebruikt om makkelijker te kunnen inschatten hoe de stenen zich ten opzichte van de dolly en van elkaar bevinden. In curling komt het immers vaak op fracties aan en is het met het blote oog niet altijd makkelijk om te bepalen welke stenen dichter bij de dolly liggen. Het gebeurt dan ook vaak dat teams tijdens een end strategische beslissingen nemen die gebaseerd zijn op verkeerde inschattingen van de onderlinge posities van de stenen. Er bestaan zeer nauwkeurige en zeer gespecialiseerde apparaten om de afstand van de stenen tot de dolly te bepalen, maar die mogen enkel gebruikt worden als een end beëindigd is. Hierdoor eindigt een end ook nooit op een gelijkspel, behalve als er geen enkele steen in het huis ligt.

Opgave

Bepaal de score van de twee teams, gegeven de posities van de stenen op het einde van een end in een curlingwedstrijd. De posities van de stenen worden voorgesteld als een reeks (een lijst of een tuple) met beschrijvingen van $$r + g$$ stenen, waarbij $$r$$ staat voor het aantal rode stenen ($$0 \leq r \leq 8$$) en $$g$$ voor het aantal gele stenen ($$0 \leq g \leq 8$$).

Elke steen wordt beschreven door een tuple $$(x, y, t)$$, waarbij $$(x, y)$$ de coördinaten zijn van het middelpunt van de steen in een assenstelsel met oorsprong in de dolly ($$x, y \in \mathbb{R}$$) en $$t$$ een string is die de kleur van de steen aangeeft (R voor rood en G voor geel).

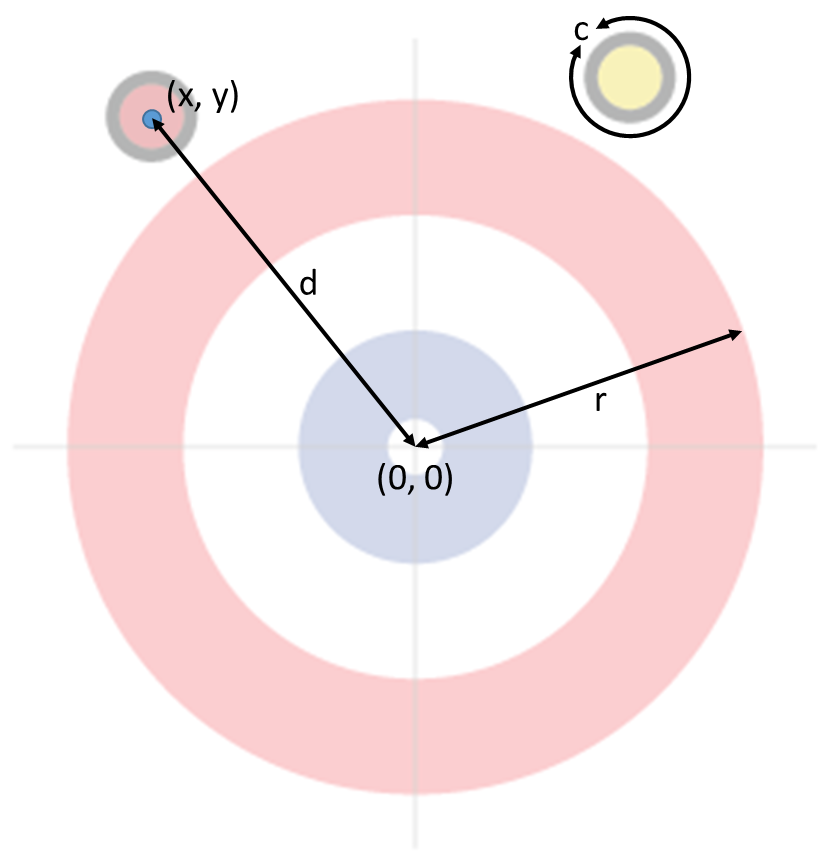
In curling draait alles om cirkels: om de score te bepalen moet je weten of een cirkelvormige steen al dan niet in het cirkelvormige huis ligt en moet je ook de afstand van een steen tot de dolly kunnen bepalen. We helpen je op weg door wat afmetingen uit de curlingsport op te lijsten, en brengen meteen ook nog wat cirkelmaten in herinnering (zie bovenstaande figuur als referentie):

• het huis is een cirkel (buitenste rand van buitenste ring) met een straal $$r$$ van 6 voet

• de stenen zijn cirkels met een omtrek $$c$$ van 36 inch

• voor de omtrek $$c$$ van een cirkel met straal $$r$$ geldt dat $$c = 2\pi r$$

• de afstand $$d$$ van de dolly tot een steen met middelpunt op positie $$(x, y)$$ is $$\sqrt{x^2 + y^2}$$

• 1 voet = 12 inch
  

• 1 inch = 0.0254 meter

Gevraagd wordt:

• Schrijf een functie binnenhuis waaraan de $$x$$- en de $$y$$-coördinaat van het middelpunt van een steen moeten doorgegeven worden in een assenstelsel met oorsprong in de dolly ($$x, y \in \mathbb{R}$$). De functie heeft ook nog een optionele derde parameter inch waaraan een Booleaanse waarde kan doorgegeven worden (standaardwaarde: True). De parameter inch geeft aan of de coördinaten van de steen worden uitgedrukt in inch (True) of in meter (False). De functie moet een Booleaanse waarde teruggeven die aangeeft of de steen in het huis ligt.

• Schrijf een functie geldigePosities waaraan de posities van de stenen op het einde van een end moeten doorgegeven worden. De functie heeft ook nog een optionele tweede parameter inch, die dezelfde betekenis heeft als bij de functie binnenhuis. De functie geldigeStenen moet een Booleaanse waarde teruggeven, die aangeeft of de gegeven posities van de stenen geldig is. Dat is het geval als er niet meer dan acht stenen zijn van elke kleur en als er geen stenen zijn die overlappen (wat fysisch gezien niet kan).

• Schrijf een functie score waaraan de posities van de stenen op het einde van een end moeten doorgegeven worden. De functie heeft ook nog een optionele tweede parameter inch, die dezelfde betekenis heeft als bij de functie binnenhuis. De functie score moet de score op het einde van die end teruggeven onder de vorm van een tuple $$(s_r, s_g)$$. Hierbij is $$s_r$$ de score van team rood en $$s_g$$ de score van team geel. Als de gegeven posities van de stenen niet geldig zijn (in de betekenis van de functie geldigePosities), dan moet een AssertionError opgeworpen worden met de boodschap ongeldige posities van stenen.

Voorbeeld

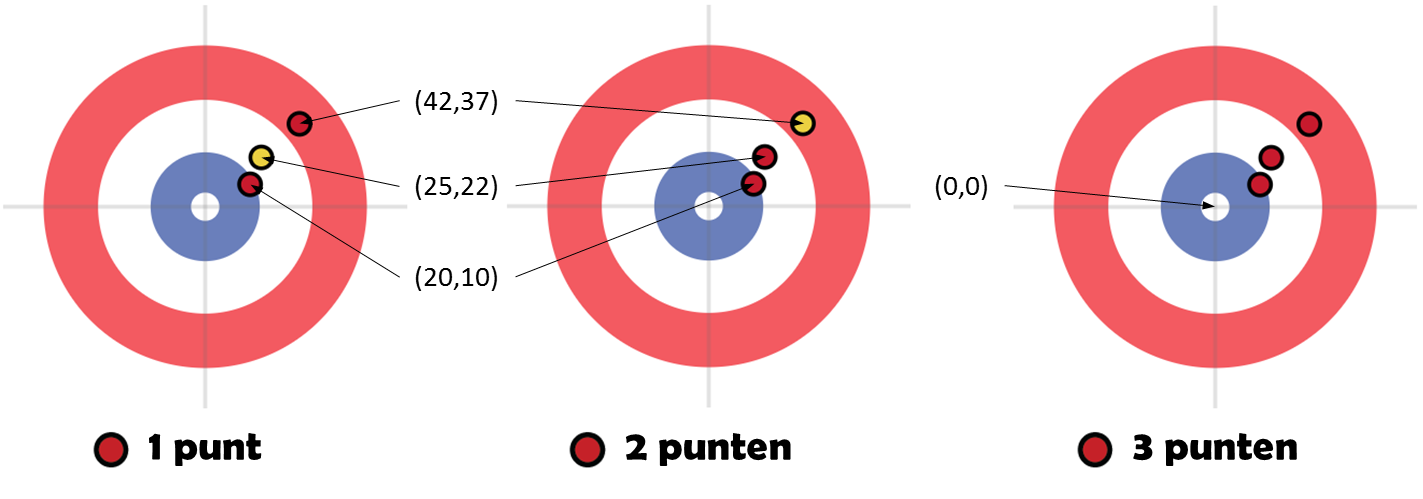
>>> binnenhuis(70.0, 0.0)
True
>>> binnenhuis(70.0, 0.0, inch=False)
False
>>> binnenhuis(78.0, 0.0)
False

>>> geldigePosities([(20.0, 10.0, 'R'), (25.0, 22.0, 'G'), (42.0, 37.0, 'R')])
True
>>> geldigePosities([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'G')])
True
>>> geldigePosities([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'R')])
True

>>> score([(20.0, 10.0, 'R'), (25.0, 22.0, 'G'), (42.0, 37.0, 'R')])
(1, 0)
>>> score([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'G')])
(2, 0)
>>> score([(20.0, 10.0, 'R'), (25.0, 22.0, 'R'), (42.0, 37.0, 'R')])
(3, 0)
>>> score([(0.508, 0.254, 'R'), (0.635, 0.5588, 'G'), (1.0668, 0.9398, 'R')], False)
(1, 0)
>>> score([(0.508, 0.254, 'R'), (0.635, 0.5588, 'R'), (1.0668, 0.9398, 'G')], inch=False)
(2, 0)
>>> score([(0.508, 0.254, 'R'), (0.635, 0.5588, 'R'), (1.0668, 0.9398, 'R')], False)
(3, 0)

Alle voorbeelden voor de functie score gebruiken stenen op dezelfde posities (de eerste drie uitgedrukt in inch de laatste drie in meter), maar met een verschillende kleur. Hieronder hebben we deze posities van de stenen grafisch voorgesteld, met hun coördinaten uitgedrukt in inch.