Steden zijn al duizenden jaren een manifestatie van de kunstzinnigheid en verbeeldingskracht van de mensheid. Ze belichamen onze sterke sociale begeerte en hunkering naar het realiseren van grootse meesterwerken. Londen, Constantinopel, Parijs, New York, het oude Rome en Tokio zijn slechts enkele van de schitterende parels die de mensheid heeft opgebouwd. Maar er zijn ook evenveel voorbeelden te vinden van iemand's visie op een betere, efficiëntere en meer indrukwekkende stad die niet verder geraakt zijn dan een hoop gebroken dromen.

Zo was Buckminster Fuller¹ bijvoorbeeld een briljante visionair, architect, wetenschapper, milieudeskundige en filosoof die in jaren 1960 met een gedurfd ontwerp voor een drijvende stad op de proppen kwam. De stad — die hij Triton City doopte — zou opgebouwd worden uit tetraëdervormige² modules, te beginnen met een drijvende buurt van 5000 inwoners met een basisschool, een supermarkt en een paar speciaalzaken. Uiteindelijk zouden drie tot vijf buurten een dorp vormen, en drie tot zeven dorpen een stad. Tijdens elke fase van de bouw zou er bijhorende infrastructuur worden toegevoegd: scholen, maatschappelijke voorzieningen, overheidsgebouwen en industrie. Een volledig opgebouwde stad zou plaats bieden aan 100.000 mensen in één enkel bouwwerk.

Fuller kreeg in eerste instantie een opdracht van een rijke Japanse beschermheer om een drijvende stad te ontwikkelen voor Tokyo Bay. De patron stierf echter in 1966, maar verassend genoeg kreeg Fuller een opdracht van het Amerikaanse ministerie van stedelijke ontwikkeling³ (HUD) voor de verdere ontwikkeling en analyse van zijn ontwerp. Fullers ontwerpen hielden onder andere rekening met het feit dat de steden bestand moesten zijn tegen tsunami's, zoveel mogelijk uitnodigden tot een buitenleven, zeewater konden ontzilten zodat het voor menselijke consumptie kon gebruikt worden, woningen zoveel mogelijk privacy moesten hebben, en gebruikgemaakt werd van tetraëdervormige modules omdat ze de grootst mogelijke oppervlakte aanbieden met het kleinst mogelijke volume. Alles — van opleiding over amusement tot ontspanning — zou deel uitmaken van de stad. Fuller beweerde ook dat de lage operationele kosten aanleiding zouden geven tot een hogere levensstandaard. Dit is een deel van het document waarmee Fuller de overheid kon overtuigen:

In the early 1960s I was commissioned by a Japanese patron to design one of my tetrahedronal floating cities for Tokyo Bay. Three-quarters of our planet Earth is covered with water, most of which may float organic cities. Floating cities pay no rent to landlords. They are situated on the water, which they desalinate and recirculate in many usefuland non-polluting ways. They are ships with all an ocean ship's technical autonomy, but they are also ships that will always be anchored. They don't have to go anywhere. Their shape and its human-life accommodations are not compromised, as must be the shape of the living quarters of ships whose hull shapes are constructed so that they may slip, fishlike, at high speed through the water and high seas with maximum economy. Floating cities are designed with the most buoyantly stable conformation of deep-sea bell-buoys. Their omni-surface-terraced, slop-faced, tetrahedronal structuring is employed to avoid the lethal threat of precipitous falls by humans from vertically sheer high-rising buildings.

Uiteindelijk stuurde de HUD de plannen door naar de Amerikaanse marine, waar ze grondig werden ontleed en verder werden geanalayseerd. Toen de eerste geruchten over Triton City zich begonnen te verspreiden, raakte de stad Baltimore geïnteresseerd in het project en startte het een petitie om de stad te laten aanleggen aan de kust voor Chesapeake Bay. Veranderingen in het federale bestuur en dat van Baltimore zorgen er echter voor dat de plannen langzaam in de vergetelheid raakten en uiteindelijk nooit gerealiseerd werden. Vandaag de dag vinden we hier en daar flauwe afkooksels van Triton City — zoals het kunstmatige eiland Kansai (Japan) dat de luchthaven van Osaka⁴ huisvest — maar die verdwijnen in het niets bij de vooropgestelde omvang van het oorspronkelijke ontwerp.

Opgave

De faculteit $$n!$$ van een getal $$n \in \mathbb{N}$$ wordt berekend als het product van alle strikt positieve natuurlijke getallen die kleiner zijn dan of gelijk aan $$n$$. \[n! = \prod_{k=1}^{n}k = 1 \times 2 \times 3 \times \cdots \times n\] Hierbij geldt dat $$0! = 1$$. De binomiaalcoëfficiënt $$\binom{n}{k}$$ is een grootheid uit de combinatoriek die aangeeft op hoeveel verschillende manieren men uit $$n \in \mathbb{N}$$ verschillende objecten er zonder terugleggen $$k \in \mathbb{N}$$ kan kiezen. \[\binom{n}{k} = \begin{cases}\frac{n!}{k!(n-k)!} & \mbox{als } 0 \leq k \leq n \\ 0 & \mbox{als } k \lt 0 \mbox{ of } k \gt n \end{cases}\] Het driehoeksgetal $$T_n$$ stelt het aantal cirkels voor die een gelijkzijdige driehoek vormen met $$n \in \mathbb{N}$$ cirkels aan elke zijde.

Grafische voorstelling van de eerste zes driehoeksgetallen. Hierbij rekenen we $$T_0 = 0$$ niet mee, omdat dit driehoeksgetal niet grafisch kan voorgesteld worden.

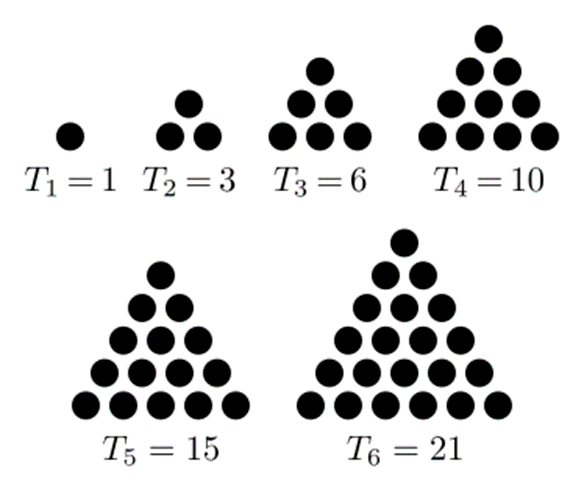
Een driehoeksgetal is dus gelijk aan de som van alle natuurlijke getallen die kleiner zijn dan of gelijk aan $$n$$. \[T_n = \sum_{k=1}^{n}k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} = \binom{n+1}{2}\] Het tetraëdergetal $$P_n$$ stelt het aantal bollen voor die een tetraëder vormen (een piramide met een driehoekige basis en drie zijden) met $$n \in \mathbb{N}$$ bollen aan elke zijde.

Een tetraëdervormige piramide met 5 bollen aan elke zijde bevat in totaal 35 bollen. Als we de lagen van boven naar onder nummeren als $$n = 1,2,\ldots,5$$ dan telt elke laag $$T_n$$ bollen.

Het $$n$$-de tetraëdergetal is gelijk aan de som van de eerste $$n$$ driehoeksgetallen. \[P_n = \sum_{k=1}^{n}T_k = \frac{n(n+1)(n+2)}{6} = \binom{n+2}{3}\] Gevraagd wordt:

Schrijf een functie faculteit waaraan een getal $$n \in \mathbb{N}$$ (int) moet doorgegeven worden. De functie moet $$n!$$ (int) teruggeven.
Schrijf een functie binomiaal waaraan twee getallen $$n, k \in \mathbb{N}$$ (int) moeten doorgegeven worden, waarvoor geldt dat $$n \geq k$$. De functie moet de binomiaalcoëfficiënt $$\binom{n}{k}$$ (int) teruggeven.
Schrijf een functie driehoeksgetal waaraan een getal $$n \in \mathbb{N}$$ (int) moet doorgegeven worden. De functie moet het $$n$$-de driehoeksgetal $$T_n$$ (int) teruggeven.
Schrijf een functie tetraedergetal waaraan een getal $$n \in \mathbb{N}$$ (int) moet doorgegeven worden. De functie moet het $$n$$-de tetraëdergetal $$P_n$$ (int) teruggeven.

Opmerking

Voor deze en alle volgende opgaven is het belangrijk dat je zoekt om bij de implementatie van functies zoveel mogelijk gebruik te proberen maken van andere functies die reeds geïmplementeerd werden. Het is ook toegelaten om bijkomende functies te definiëren om daarmee het verdeel-en-heers-principe⁵ toe te passen.

Voorbeeld

>>> faculteit(10)
3628800
>>> faculteit(32)
263130836933693530167218012160000000

>>> binomiaal(7, 3)
35
>>> binomiaal(12, 4)
495

>>> driehoeksgetal(10)
55
>>> driehoeksgetal(32)
528

>>> tetraedergetal(10)
220
>>> tetraedergetal(32)
5984

Opgave

Opmerking

Voorbeeld

Epiloog