Programmeer de gevectoriseerde periodieke "zaagtand"-functie $$z(x), x \in \mathbb{R}$$, met als voorschrift:

$$ \vdots $$
$$ z(x) = x + 2a, -2a \le x \lt -a $$
$$ z(x) = x + a, -a \le x \lt 0 $$
$$ z(x) = x , 0 \le x \lt a $$
$$ z(x) = x - a , a \le x \lt 2a $$
$$ z(x) = x - 2a , 2a \le x \lt 3a $$
$$ \vdots $$

Deze functie neemt dus de waarde $$x$$ aan in het interval $$[0, a[$$, en is periodiek met periode $$a$$.

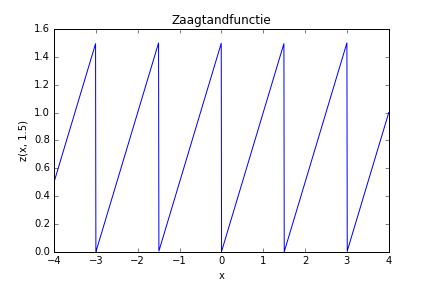
Noem de Python-functie $$\verb!zaagtand()!$$, en voorzie 2 argumenten, repectievelijk $$x$$ en $$a$$. Zorg dat ze inderdaad gevectoriseerd is: indien het eerste argument een NumPy-rij is, is het resultaat een NumPy-rij, en indien het eerste argument een reëel getal is, is het resultaat ook een reëel getal. Het tweede argument is steeds een strikt positief reëel getal. Je mag hierbij aannemen dat het eerste argument geen sprongpunten van de functie bevat.

TIP : denk aan de gehele deling.

Voorbeeld

 
zaagtand(np.array([0.1, 0.5, 1.0, 1.6, 2.0, 2.5, 3.1]), 1.5) = [0.1 0.5 1.0 0.1 0.5 1.0 0.1]
zaagtand(5.0, 1.5) = 0.5