De koning van een kleine dwergstaat nodigt 1000 senatoren uit op zijn jaarlijkse feest dat morgen plaatsvindt. Zoals de traditie het voorschrijft, brengt elke senator een fles wijn mee voor de koning. Uit goede bron verneemt de koningin echter dat één van de senatoren probeert om de koning te vermoorden door hem een vergiftigde fles wijn te schenken. Spijtig genoeg is de identiteit van de senator onbekend, en blijkt het onmogelijk om via chemische analyse te achterhalen welke fles een gifstof bevat.

In de kerker van het koninklijk paleis zitten echter 10 gevangenen die op het punt staan om geëxecuteerd te worden. De koning besluit om ze als proefpersonen te gebruiken om de vergiftigde fles wijn op te sporen. Helaas heeft het gif geen enkele effect op de gevangenen tot 24 uur na inname, waarna een gevange die vergiftigd werd onmiddellijk sterft. De koning moet tegen morgen zien te achterhalen welke fles wijn vergiftigd werd, zodat de festiviteiten kunnen doorgaan zoals gepland. Daardoor heeft hij slechts tijd om de gevangenen één keer te laten proeven. Hoe kan de koning de wijn aan de gevangenen serveren om over 24 uur zekerheid te hebben welke fles vergiftigd werd?

Hier is een mogelijke oplossing. Er zijn 1000 flessen wijn, waarvan er één vergiftigd werd en op de een of andere manier moeten we alle flessen wijn zien te testen met slechts 10 proefpersonen. Hoe we de flessen wijn ook toedienen aan de gevangenen, we moeten ervoor zorgen dat we de informatie over de gevangenen die sterven door vergiftiging gebruiken als een code om de vergiftigde fles wijn op te sporen.

Aangezien we slechts 24 uur de tijd hebben om de wijn te testen, weten we dat er niet genoeg tijd en/of genoeg gevangen zijn om hen de wijn één per één te laten proeven. Vermoedelijk was je zelf ook al tot deze vaststelling gekomen en slaat hier dus de verwarring toe.

Hoe krijgen we in hemelsnaam alle flessen getest? Wel, we zullen op de ene of andere manier de gevangenen dronken moeten voeren. Dat kan ik je nu al verzekeren. Nee, serieus, we zijn op zoek naar een systematische manier om de wijn aan de gevangenen te geven zodat er 1000 verschillende combinaties zijn! Laat ons eerst de flessen wijn nummeren van 0-999 zodat we ze van elkaar kunnen onderscheiden. Daarna zetten we ook de gevangen op een rij en labelen ze met de letters A-J.

We laten gevangene A nu een beetje wijn drinken van elke andere fles, te beginnen met de tweede fles (de fles met #1). Met andere woorden, gevangene A laten we drinken van de flessen #1, #3, #5, …

Vervolgens laten we gevangene B drinken om het andere paar flessen. Met andere woorden, we slaan de flessen #0 en #1 over en laten gevange B drinken van de flessen #2 en #3. Daarna slaan we opnieuw de flessen #4 en #5 over en laten hem drinken van de flessen #6 en #7. We blijven dit patroon herhalen.

Gevangene C laten we om de andere reeks van vier flessen drinken. Dit komt neer op het feit dat gevangene C drinkt van de flessen #4-7 (#0-3 slaan we over), #12-15 (#8-11 slaan we over), #20-23, …

Begin je het patroon te zien? Verdubbel telkens het aantal flessen in de reeks die elke gevange moet overslaan en daarna drinken. Gevangene D drinkt om de acht flessen, gevangene E om de 16 flessen, gevangene F om de 32 flessen, gevangene G om de 64 flessen, gevangene H om de 128 flessen, gevangene I om de 256 flessen en ten slotte drinkt gevangene J niet van de eerste 512 flessen.

Op dit punt valt je waarschijnlijk iets op waarmee je vertrouwd bent. Het toekennen van de flessen aan de gevangen gebeurt volgens de machten van 2.

We hebben nu dus een manier gevonden waarmee we de wijn uit de flessen aan de gevangen kunnen toedienen zodat er voldoende combinaties mogelijk zijn. Het volstaat nu om 24 uur te wachten om te zien welke gevangenen het loodje leggen.

Maar hoe kunnen we daarmee achterhalen welke fles wijn vergiftigd was? Wel, we beschouwen het patroon van de vergiftigde gevangenen als een binair getal van 10 cijfers. We doen dit door boven elke gevangene die overleden is een 1 te schrijven, en boven elke gevangene die nog leeft een 0. Vooraleer we het resultaat decoderen, keren we eerst de volgorde van de gevangenen om, zodat ze overeenkomen met hun plaats in het binair talstelsel.

Daar gaan we. Beschouw eerst en vooral het geval waarbij blijkt dat geen enkele gevangene na 24 uur is overleden. Welke fles was er dan vergiftigd? In dat geval moet het de eerste fles (fles #0) geweest zijn, aangezien dit de enige fles is waarvan geen enkele gevangene heeft gedronken. We kunnen dit ook afleiden uit ons diagram: aangezien er geen enkele gevangene is overleden, plaatsen we een 0 boven elk van de gevangenen. Het binaire getal $$(0000000000)_2$$ is gelijk aan $$(0)_{10}$$ in het decimale talstelsel.

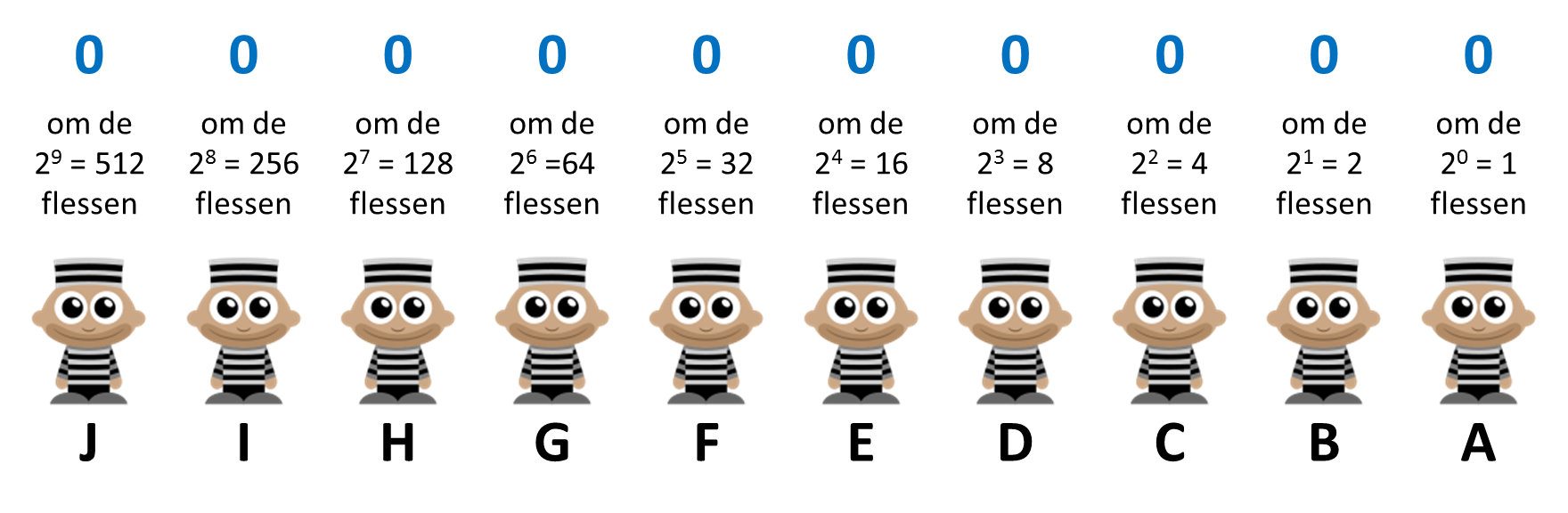
Veronderstel nu dat enkel gevangene A is overleden door vergiftiging. In dit geval plaatsen we een 1 boven gevangene A en een 0 boven alle andere gevangenen.

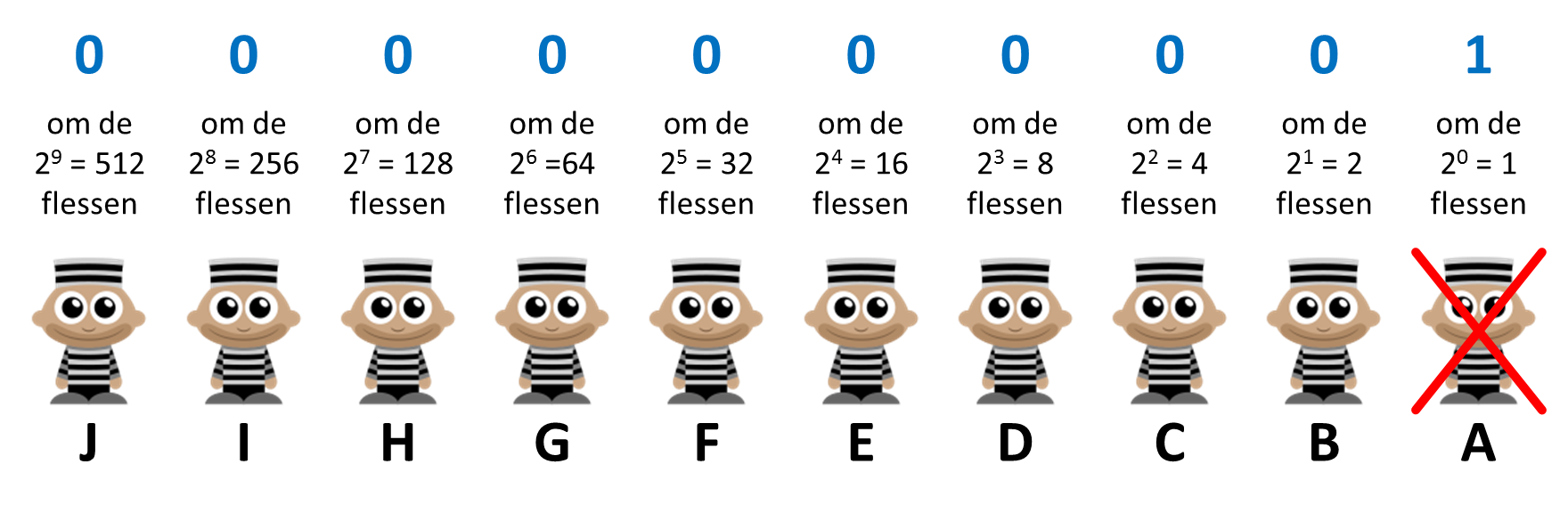
Als we het binaire getal $$(0000000001)_2$$ vertalen naar het decimale talstelsel, dan krijgen we $$(1)_{10}$$. Daaruit leiden we af dat fles #1 vergiftigd was. Dit bevestigt wat we eigenlijk al wisten, omdat gevangene A de enige is die van fles #1 heeft gedronken (onthoud dat gevange A heeft gedronken van de flessen #1, #3, #5, …).

Was als de gevangenen A, C, E, G en I vergiftigd blijken te zijn?

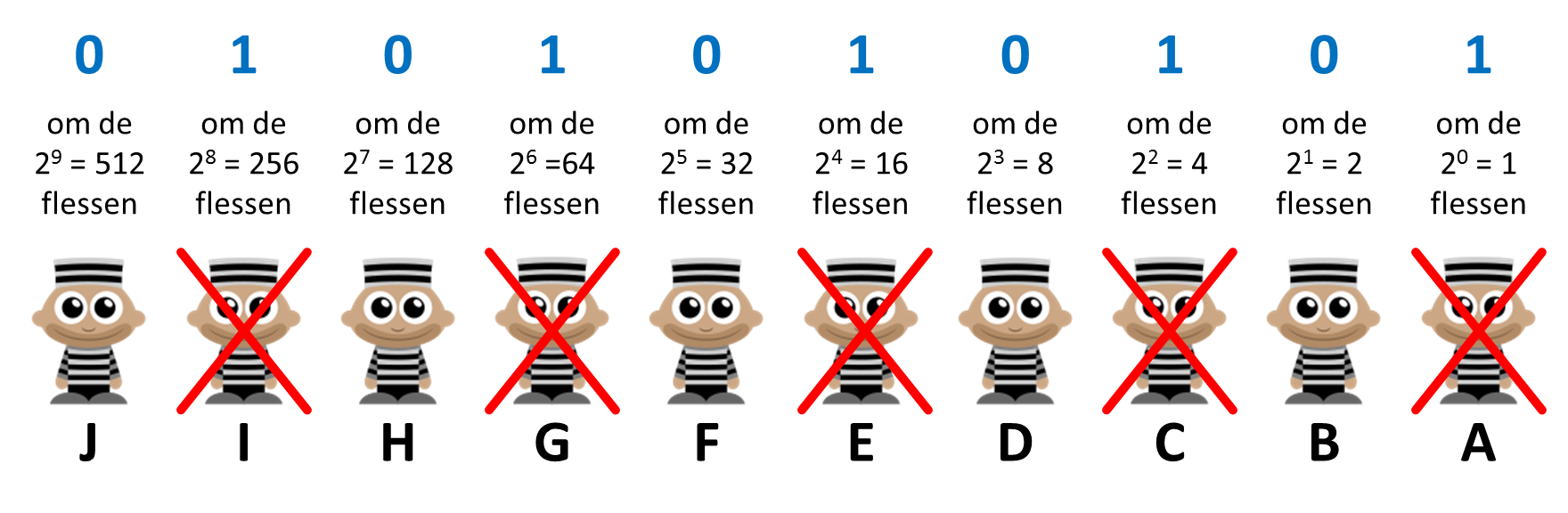
Vertaal het binaire getal $$(0101010101)_2$$ naar het decimaal talstelsel om te achterhalen welke fles er vergiftigd werd. \[(0101010101)_2 = 2^8 + 2^6 + 2^4 + 2^2 + 2^0 = 256 + 64 + 16 + 4 + 1 = 341\] Daaruit volgt dus dat fles #341 vergiftigd is.

Vrij vernuftig, niet? Omdat er 10 gevangenen zijn en elke gevange heeft twee toestanden (levend of dood), levert dit systeem ons in totaal $$2^{10} = 1024$$ verschillende combinaties op. Dat is meer dan voldoende combinaties aangezien er slechts 1000 flessen wijn zijn.

Invoer

De eerste regel van de invoer bevat een getal $$n \in \mathbb{N}$$ dat aangeeft hoeveel gevangenen er gestorven zijn na 24 uur. Daarna volgen de $$n$$ hoofdletters waarmee de overleden gevangenen gelabeld werden, elk op een afzonderlijke regel. Deze hoofdletters staan niet noodzakelijk in alfabetische volgorde.

Uitvoer

De uitvoer bestaat uit de tekst Fles #n is vergiftigd., waarbij n moet ingevuld worden met het nummer van de vergiftigde fles.

Voorbeeld

Invoer:

5
A
C
E
G
I

Uitvoer:

Fles #341 is vergiftigd.