Bereken de oppervlakte van een driehoek op basis van de coördinaten van de hoekpunten. Je mag er van uitgaan dat alleen correct invoer ingegeven wordt. Gebruik hiervoor de formule van Heron:
\[oppervlakte = \sqrt{s(s-a)(s-b)(s-c)}\] \[s = \frac{a + b + c}{2}\]Hierbij zijn:
- \(a\), \(b\) en \(c\): de zijden van de driehoek.
- \(s\): de halve omtrek.
Afstand tussen twee punten
De afstand tussen twee punten \(A (x_1,y_1)\) en \(B (x_2,y_2)\) kan je berekenen met de formule voor de euclidische afstand:
\[afstand = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\]
Invoer
De coördinaten worden in deze volgord ingegeven:
x-coördinaat punt A:
y-coördinaat punt A:
x-coördinaat punt B:
y-coördinaat punt B:
x-coördinaat punt C:
y-coördinaat punt C:
Uitvoer
Print bij de uitvoer op deze manier "De oppervlakte van de driehoek is {oppervlakte}.
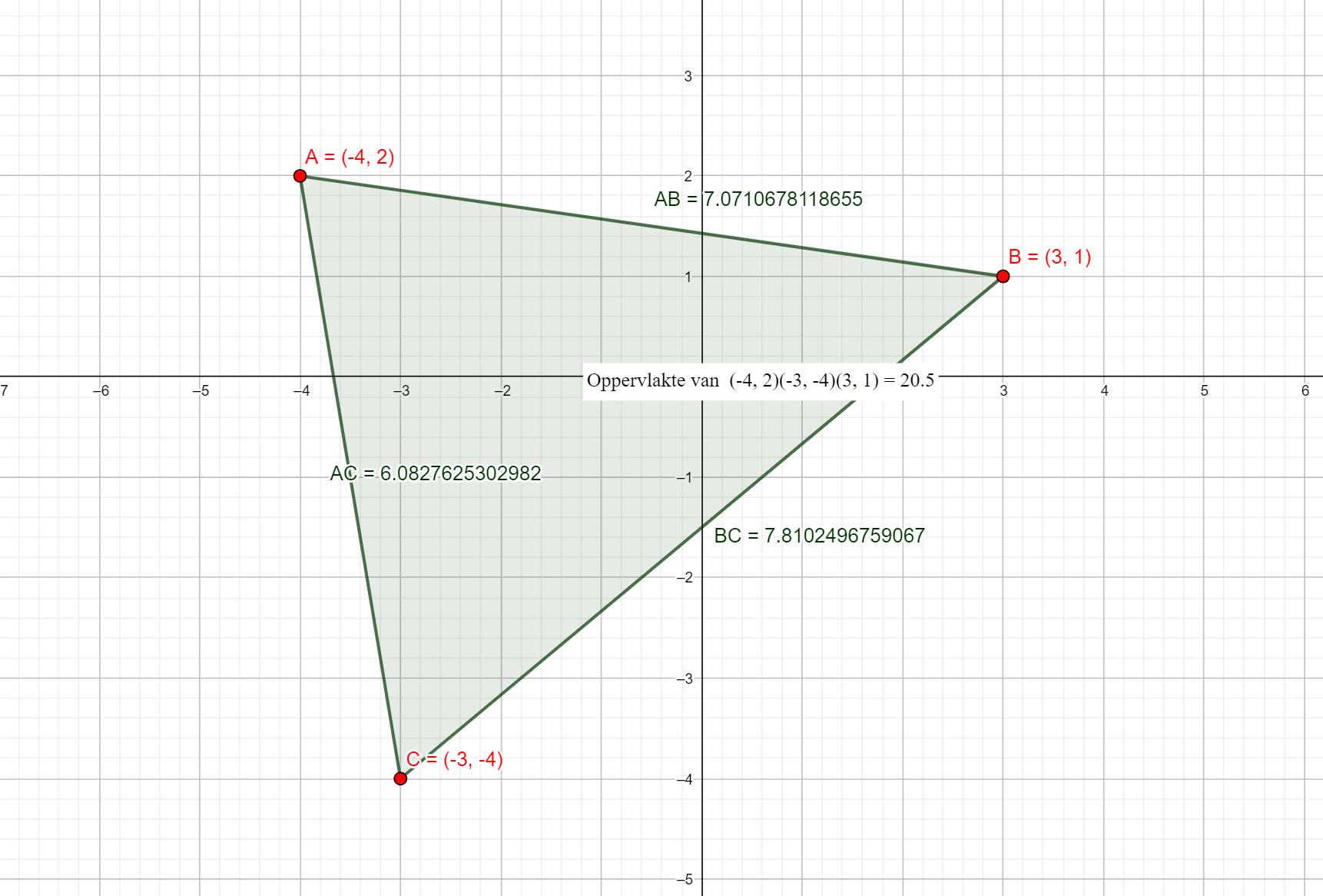
Voorbeeld1
Invoer
x-coördinaat eerste hoekpunt: -4
y-coördinaat eerste hoekpunt: 2
x-coördinaat tweede hoekpunt: 3
y-coördinaat tweede hoekpunt: 1
x-coördinaat derde hoekpunt: -3
y-coördinaat derde hoekpunt: -4
Uitvoer
De oppervlakte van de driehoek is 20.499999999999993