Vergeet alles wat je dacht te weten over het vereenvoudigen van breuken — onderstaande voorbeelden tonen aan dat je breuken simpelweg kunt vereenvoudigen door alle gemeenschappelijk cijfers in de teller en de noemer te schrappen:

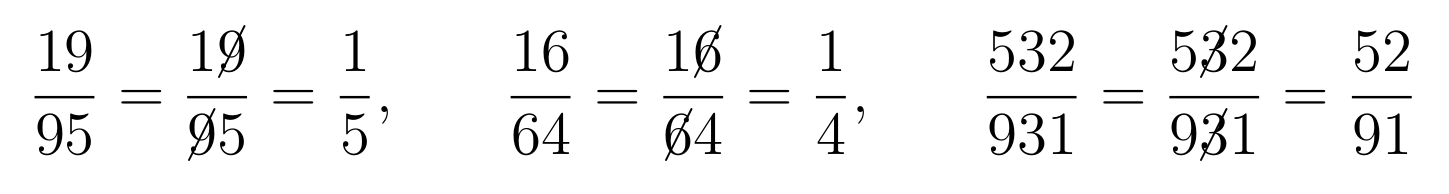
Niet overtuigd? Dan heeft je buikgevoel het inderdaad bij het rechte eind! Bovenstaande breuken zijn enkel maar speciale gevallen waarvoor de reductio ad absurdum methode op een geldige manier kan toegepast worden, maar voor de meeste andere breuken levert de methode een verschillend resultaat op. Probeer het bijvoorbeeld maar eens uit op de breuk $$\frac{12}{13}$$.

Opgave

Voor deze opgave moet moet je nagaan of het toegelaten is om de techniek van reductio ad absurdum toe te passen op een gegeven breuk. Hiervoor ga je als volgt te werk:

• Schrijf een functie gelijkeBreuk waaraan vier getallen $$t_1, n_1, t_2, n_2 \in \mathbb{N}_0$$ moeten doorgegeven worden. De functie moet een Booleaanse waarde teruggeven die aangeeft of de breuken $$\frac{t_1}{n_1}$$ en $$\frac{t_2}{n_2}$$ al dan niet gelijk zijn. Merk op dat het omwille van afrondingsfouten onveilig is om de gelijkheid te testen door reële delingen uit te voeren. In plaats daarvan kan je best eerst de breuken op gelijke noemer plaatsen alvorens ze met elkaar te vergelijken.

• Schrijf een functie reductie waaraan twee getallen $$t, n \in \mathbb{N}_0$$ moeten doorgegeven worden die respectievelijk de teller en de noemer van een breuk voorstellen. Voor elk cijfer uit de teller dat ook in de noemer voorkomt, moet de functie het meest links voorkomen van dat cijfer schrappen uit zowel de teller als de noemer, en dit totdat de teller en de noemer geen gemeenschappelijke cijfers meer hebben. De functie moeten als resultaat twee integers teruggeven die respectievelijk de teller en de noemer voorstellen na het schrappen van de gemeenschappelijke cijfers. Indien alle cijfers uit de teller geschrapt werden, dan moet de eerste waarde die teruggegeven wordt -1 zijn. Hetzelfde geldt voor de tweede waarde die wordt teruggegeven indien alle cijfers uit de noemer geschrapt werden.

• Gebruik de functies gelijkeBreuk en reductie om een functie geldigeReductie te schrijven. Aan deze functie moeten twee getallen $$t, n \in \mathbb{N}_0$$ doorgegeven worden die respectievelijk de teller en de noemer van een breuk voorstellen. De functie geldigeReductie moet hetzelfde resultaat teruggeven als de functie reductie indien de gereduceerde breuk geldig blijkt te zijn. Dit laatste is het geval als de volgende voorwaarden voldaan zijn:

• na reductie blijven er nog cijfers over in de teller en de noemer

• na reductie mag de noemer niet nul zijn (de noemer van een breuk mag niet nul zijn)

• de waarde van de breuk na reductie is dezelfde als de waarde van de breuk voor reductie (conform de definitie van gelijkheid zoals geïmplementeerd door de functie gelijkeBreuk)

Wanneer reductie een ongeldige breuk zou opleveren, dan moet de functie geldigeReductie de oorspronkelijke teller en noemer teruggeven zoals die aan de functie doorgegeven werden.

Voorbeeld

>>> gelijkeBreuk(19, 95, 1, 5)
True
>>> gelijkeBreuk(532, 931, 52, 91)
True
>>> gelijkeBreuk(12, 13, 2, 3)
False

>>> reductie(19, 95)
(1, 5)
>>> reductie(532, 931)
(52, 91)
>>> reductie(2349, 9396)
(24, 96)
>>> reductie(12, 13)
(2, 3)
>>> reductie(11, 10)
(1, 0)
>>> reductie(123, 3214)
(-1, 4)

>>> geldigeReductie(19, 95)
(1, 5)
>>> geldigeReductie(532, 931)
(52, 91)
>>> geldigeReductie(2349, 9396)
(24, 96)
>>> geldigeReductie(12, 13)
(12, 13)
>>> geldigeReductie(11, 10)
(11, 10)
>>> geldigeReductie(123, 3214)
(123, 3214)