Neem een willekeurige bitstring bestaande uit $$m \in \mathbb{N}_0$$ opeenvolgende enen en nullen. Schrijf de enen en nullen van de bitstring in wijzerzin langs een cirkel. Reproduceer de bitstring door de enen en nullen nogmaals in wijzerzin langs een cirkel te schrijven, concentrisch met de overeenkomstige enen en nullen van de eerste cirkel. Roteer de binnenste cirkel over $$n \in \mathbb{Z}$$ posities. Als $$n > 0$$ dan roteren we over $$n$$ posities in wijzerzin. Als $$n < 0$$ dan roteren we over $$|n|$$ posities in tegenwijzerzin.
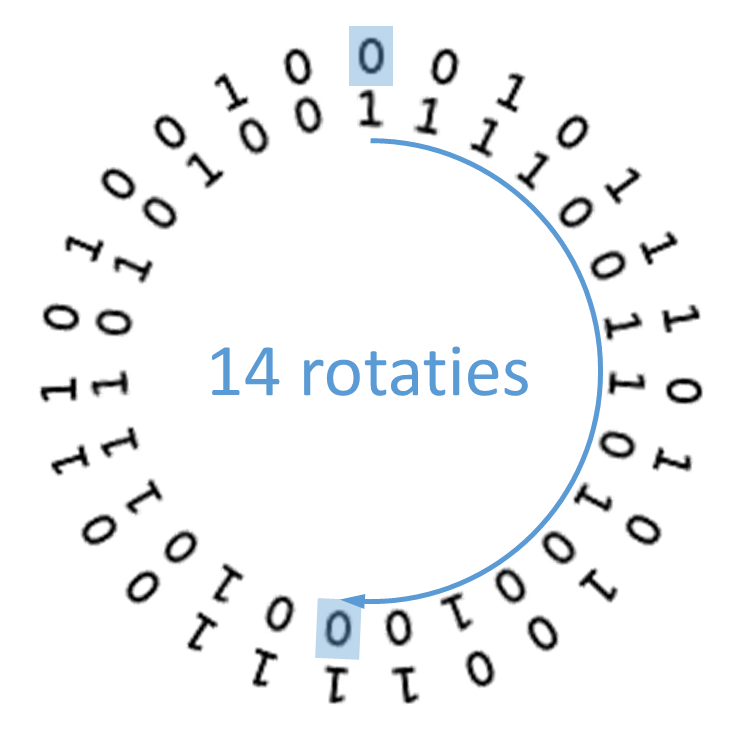
Tel nu het aantal posities waarbij er een 0 tegenover een 1 staat.

Dit aantal zal altijd even zijn.
Invoer
Een regel met een bitstring bestaande uit $$m \in \mathbb{N}_0$$ opeenvolgende enen en nullen, gevolgd door een regel met een getal $$n \in \mathbb{Z}$$.
Uitvoer
Een regel met de gegeven bitstring gevolgd door een regel met de gegeven bitstring geroteerd over $$n$$ posities. Tussen die twee regels staat nog een regel die voor elk van de $$m$$ overeenkomstige bitparen van de twee bitstrings aangeeft met een verticale streep (|) dat er een 0 tegenover een 1 staat, of met een spatie dat dit niet het geval is. Na die $$m$$ verticale strepen en spaties volgt nog een spatie en tussen ronde haakjes het aantal posities waarbij er een 0 tegenover een 1 staat.
Voorbeeld
Invoer:
001011101010011110011010010
14Uitvoer:
001011101010011110011010010
|| ||| |||| |||| | || (16)
111100110100100010111010100