Toen Matt Parker1 een tandheelkundige operatie moest ondergaan, vroeg hij op Twitter naar een raadsel waarmee hij zichzelf wat afleiding kon bezorgen. Een van zijn vrienden tweette hem de volgende uitdaging:
Rangschik alle cijfers van 1 tot en met 9 in een bepaalde volgorde zodat de eerste twee cijfers van het bekomen getal een veelvoud van 2 vormen, de eerste drie cijfers een veelvoud van 3, de eerste vier cijfers een veelvoud van 4, enzoverder, en ten slotte ook het volledige getal een veelvoud van 9 is.
Als je de cijfers in hun conventionele volgorde laat staan, dan bekom je het getal 123456789. Maar dat is geen geldige oplossing: 12 is deelbaar door 2 en 123 is deelbaar door 3, maar 1234 is niet deelbaar door 4. Matt Parker zei hierover:
Tegen het einde van mijn ingreep had ik al enkele cijfers van de oplossing gevonden, maar zeker nog niet allemaal. En blijkbaar mag je dus niet in de stoel van de tandarts blijven zitten als de operatie afgelopen is.
Thuis werkte hij de rest van de oplossing uit, die bovendien ook uniek bleek te zijn. Wat is die oplossing?
Opgave
Bovenstaand raadsel kan veralgemeend worden door de voorwaarde te laten vallen dat alle cijfers van 1 tot en met 9 juist één keer moeten voorkomen. We zeggen dat een natuurlijk getal met cijfers abcde… polydeelbaar is, als het voldoet aan de volgende voorwaarden:
-
het eerste cijfer a is niet 0 (het getal heeft met andere woorden geen voorloopnullen)
-
het getal dat gevormd wordt door de eerste twee cijfers ab is een veelvoud van 2
-
het getal dat gevormd wordt door de eerste drie cijfers abc is een veelvoud van 3
-
het getal dat gevormd wordt door de eerste vier cijfers abcd is een veelvoud van 4
-
enzoverder
Zo is 345654 bijvoorbeeld een polydeelbaar getal, maar 123456 is niet polydeelbaar omdat 1234 geen veelvoud is van 4. Er zijn in totaal 2492 polydeelbare getallen met 9 cijfers, maar slechts één daarvan voldoet aan de bijkomende voorwaarde van het raadsel: 381654729. Gevraagd wordt:
-
Schrijf een functie langste_polydeelbare_prefix waaraan een natuurlijk getal $$n \in \mathbb{N}_0$$ (int) moet doorgegeven worden. De functie moet de langste polydeelbare prefix van $$n$$ teruggeven (int). Hierbij bestaat een prefix van een getal uit een reeks opeenvolgende cijfers aan het begin van het getal: 12345 is een prefix van het getal 123456789, maar 4567 of 789 niet.
-
Schrijf een functie ispolydeelbaar waaraan een natuurlijk getal $$n \in \mathbb{N}_0$$ (int) moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of $$n$$ polydeelbaar is.
-
Schrijf een functie polydeelbare_uitbreidingen waaraan een natuurlijk getal $$n \in \mathbb{N}_0$$ (int) moet doorgegeven worden. De functie moet teruggeven hoeveel (int) polydeelbare getallen we bekomen door op het einde van $$n$$ nog een extra cijfer (0 tot en met 9) toe te voegen. Zo heeft 12 bijvoorbeeld 4 polydeelbare uitbreidingen: 120, 123, 126 en 129.
Voorbeeld
>>> langste_polydeelbare_prefix(1234356789)
123
>>> langste_polydeelbare_prefix(381654729)
381654729
>>> langste_polydeelbare_prefix(381654728)
38165472
>>> ispolydeelbaar(1234356789)
False
>>> ispolydeelbaar(381654729)
True
>>> ispolydeelbaar(381654728)
False
>>> polydeelbare_uitbreidingen(12)
4
>>> polydeelbare_uitbreidingen(23)
0
>>> polydeelbare_uitbreidingen(381654729)
1
Epiloog
Hoeveel polydeelbare getallen zijn er? Als $$n$$ een polydeelbaar getal is met $$k - 1$$ cijfers, dan kunnen we het uitbreiden tot een polydeelbaar getal van $$k$$ cijfers als er een getal tussen $$10n$$ en $$10n + 9$$ bestaat dat deelbaar is door $$k$$. Als $$k$$ kleiner dan of gelijk is aan 10, dan is het altijd mogelijk om een polydeelbaar getal van $$k - 1$$ cijfers op deze manier uit te breiden tot een polydeelbaar getal van $$k$$ cijfers, en is het goed mogelijk dat er zelfs meer dan één polydeelbare uitbreiding is. Als $$k$$ groter is dan 10, dan is het niet altijd mogelijk om $$n$$ op deze manier uit te breiden tot een polydeelbaar getal, en naarmate $$k$$ groter wordt daalt ook de kans dat een gegeven polydeelbaar getal van $$k$$ cijfers uitbreidbaar is.
Gemiddeld kan elk polydeelbaar getal van $$k - 1$$ cijfers op $$\frac{10}{k}$$ verschillende manieren uitgebreid worden tot een polydeelbaar getal van $$k$$ cijfers. Dit geeft ons de volgende schatting van het aantal polydeelbare getallen van $$k$$ cijfers, dat we aanduiden door $$F(k)$$: \[ F(k) \approx \frac{9 \times 10^{k - 1}}{k!} \] Als we dit optellen over alle waarden van $$k$$, dan suggereert deze schatting dat het totaal aantal polydeelbare getallen bij benadering gelijk is aan \[ \frac{9 \times (e^{10} - 1)}{10} \approx 19823 \] Blijkt dat dit een onderschatting is met ongeveer 3% van het werkelijk aantal polydeelbare getallen. We kunnen de werkelijke waarden van $$F(k)$$ bepalen door het aantal polydeelbare getallen met een gegeven lengte te tellen:
| $$k$$ | $$F(k)$$ | schatting van $$F(k)$$ |
|---|---|---|
| 1 | 9 | 9 |
| 2 | 45 | 45 |
| 3 | 150 | 150 |
| 4 | 375 | 375 |
| 5 | 750 | 750 |
| 6 | 1200 | 1250 |
| 7 | 1713 | 1786 |
| 8 | 2227 | 2232 |
| 9 | 2492 | 2480 |
| $$k$$ | $$F(k)$$ | schatting van $$F(k)$$ |
|---|---|---|
| 10 | 2492 | 2480 |
| 11 | 2225 | 2255 |
| 12 | 2041 | 1879 |
| 13 | 1575 | 1445 |
| 14 | 1132 | 1032 |
| 15 | 770 | 688 |
| 16 | 571 | 430 |
| 17 | 335 | 253 |
| 18 | 180 | 141 |
| $$k$$ | $$F(k)$$ | schatting van $$F(k)$$ |
|---|---|---|
| 19 | 90 | 74 |
| 20 | 44 | 37 |
| 21 | 18 | 17 |
| 22 | 12 | 8 |
| 23 | 6 | 3 |
| 24 | 3 | 1 |
| 25 | 1 | 1 |
De verdeling van polydeelbare getallen kan ook op een grafische manier voorgesteld worden:
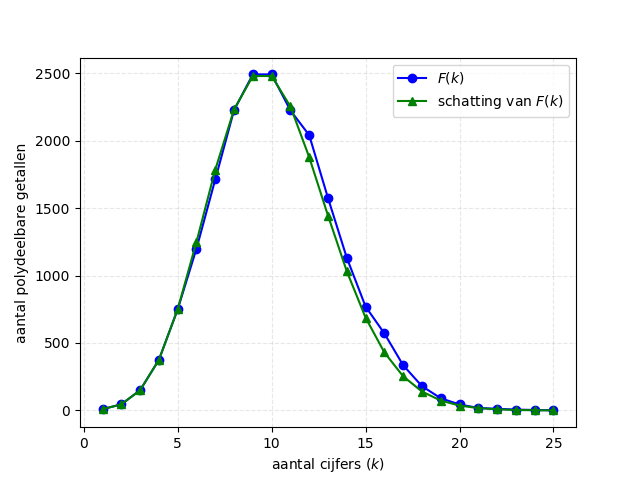
In totaal zijn er 20456 polydeelbare getallen. Het langste polydeelbare getal heeft 25 cijfers:
3608528850368400786036725
Naast de voorwaarde die wordt opgelegd in het raadsel uit de inleiding van deze opgave, kunnen we ook nog polydeelbare getallen zoeken die voldoen aan andere bijkomende voorwaarden. Zo is het langste polydeelbare getal dat enkel bestaat uit even cijfers bijvoorbeeld gelijk aan
48000688208466084040
We kunnen ook op zoek gaan naar polydeelbare getallen die palindromen zijn. Het langste palindromische polydeelbare getal is
30000600003