Game of Life is een spel dat in 1970 werd uitgevonden door de Britse wiskundige John Conway. Het werd gepubliceerd in Scientific American¹ onder de rubriek Mathematical Games van Martin Gardner. Deze spelvorm is een voorbeeld van een cellulaire automaat en wijkt af van andere spelletjes zoals monopoly, risk of schaken, in die zin dat er geen spelers zijn en dat men niet echt kan winnen of verliezen.

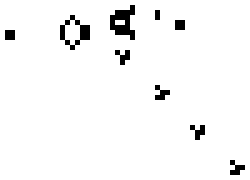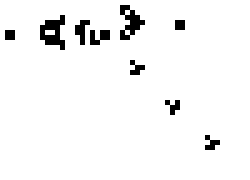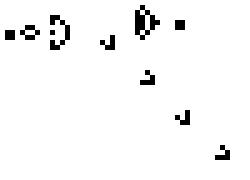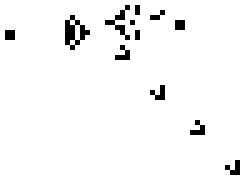
Het spelbord bestaat uit een rechthoekig rooster, en kan dus in een computerprogramma worden voorgesteld door een lijst van lijsten. Nadat een aantal cellen van het rooster is ingekleurd, begint het spel. Game of Life doorloopt verschillende 'generaties'. Om te bepalen of een cel in de volgende generatie gekleurd is of juist niet, wordt er een aantal regels toegepast aan de hand van de status (levend of dood) die de buurcellen hebben. Hierbij heeft elke cel in het rooster maximaal 8 buurcellen, behalve de cellen op de rand van het rooster die minder dan 8 buren hebben. Conway heeft veel geëxperimenteerd met verschillende reeksen regels om een goede balans te vinden. Met de verkeerde regels zouden namelijk meer velden (in Game of Life 'cellen' genoemd) gekleurd ('geboren') dan wit ('dood') worden, waardoor het hele hokjesveld ('rooster') gekleurd wordt. Of andersom: er gaan zoveel velden dood dat het hele gebied wit wordt. De meest gebruikte regels zijn de volgende:

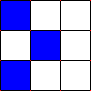
Als een levende cel door 2 of 3 levende buurcellen omgeven wordt, blijft deze cel ook in de volgende generatie levend, zoals de middelste cel in de onderstaande afbeelding. In dit voorbeeld blijft de middelste cel gekleurd, want de cel wordt omgeven door 2 andere gekleurde cellen.
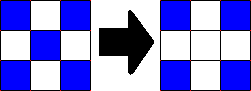
Als een levende cel door 4 of meer levende buurcellen omgeven wordt, dan gaat deze cel dood door overbevolking (dat wil zeggen, de cel wordt wit). Als een levende cel door minder dan twee levende buurcellen omgeven wordt, gaat deze cel ook dood, maar dan door eenzaamheid. Dit wordt geïllustreerd in de onderstaande afbeelding. In dit voorbeeld gaat de middelste cel dood, want de cel wordt door meer dan 3 of minder dan 2 gekleurde cellen omgeven.
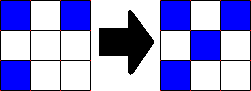
Als een dode cel wordt omgeven door precies 3 levende buurcellen, dan wordt deze dode cel in de volgende generatie levend ('geboren'), zoals aangegeven in de afbeelding hieronder. In dit voorbeeld wordt de middelste cel gekleurd, want de cel wordt door exact 3 gekleurde cellen omgeven.

Al deze transformaties geschieden gelijktijdig voor alle cellen. De kunst van het spel is patronen te bedenken die bijzonder gedrag vertonen. Er zijn stabiele patronen (eenvoudigste voorbeeld: een blokje van vier). Er zijn patronen die heen en weer gaan tussen twee of meer standen. Er zijn patronen die op den duur verdwijnen of veranderen in een stabiel patroon. Interessant zijn de patronen die zich verplaatsen, zoals de glider en de glider gun.

Opgave

Schrijf een functie toonGeneratie die de toestand van een gegeven generatie afdrukt. Deze functie heeft één verplicht argument: een lijst van lijsten die een rechthoekig rooster voorstelt. De geneste lijsten hebben allemaal dezelfde lengte en bevatten enkel Booleaanse waarden. Een generatie wordt dus voorgesteld door een lijst van rijen, waarbij elke rij zelf ook door een lijst wordt voorgesteld. Op positie $$n$$ staat er True als de cel op kolom $$n$$ in die rij leeft. Anders staat er False. De levende cellen worden bij het afdrukken voorgesteld door de letter X en de dode cellen worden voorgesteld door de letter O (niet het cijfer nul!!).
Schrijf een functie aantalBuren die voor een gegeven generatie en een gegeven cel teruggeeft hoeveel levende buren die cel heeft. Deze functie heeft drie verplichte argumenten: het eerste argument is de gegeven generatie, het tweede argument de rij en het derde argument de kolom van de cel waarvan de buren worden opgevraagd.
Gebruik de functie aantalBuren om een functie volgendeGeneratie te schrijven, dat de volgende generatie teruggeeft voor een gegeven generatie. Deze nieuwe generatie wordt op dezelfde manier voorgesteld als de gegeven generatie, namelijk als een lijst van lijsten. De gegeven generatie wordt als argument aan de functie doorgegeven, en wordt door de functie ook niet gewijzigd.

Onderstaand voorbeeld illustreert hoe deze functie moeten kunnen gebruikt worden.

Voorbeeld

>>> generatie = [[True] + [False] * 7 for _ in range(6)]
>>> toonGeneratie(generatie)
X O O O O O O O
X O O O O O O O
X O O O O O O O
X O O O O O O O
X O O O O O O O
X O O O O O O O

>>> aantalBuren(generatie, 0, 0)
1
>>> aantalBuren(generatie, 1, 1)
3
>>> aantalBuren(generatie, 2, 2)
0

>>> volgende = volgendeGeneratie(generatie)
>>> toonGeneratie(volgende)
O O O O O O O O
X X O O O O O O
X X O O O O O O
X X O O O O O O
X X O O O O O O
O O O O O O O O
>>> volgende = volgendeGeneratie(volgende)
>>> toonGeneratie(volgende)
O O O O O O O O
X X O O O O O O
O O X O O O O O
O O X O O O O O
X X O O O O O O
O O O O O O O O
>>> volgende = volgendeGeneratie(volgende)
>>> toonGeneratie(volgende)
O O O O O O O O
O X O O O O O O
O O X O O O O O
O O X O O O O O
O X O O O O O O
O O O O O O O O
>>> volgende = volgendeGeneratie(volgende)
>>> toonGeneratie(volgende)
O O O O O O O O
O O O O O O O O
O X X O O O O O
O X X O O O O O
O O O O O O O O
O O O O O O O O