Het algoritme van Floyd gebruikt dynamisch programmeren om de kortste paden tussen elk paar toppen in een graaf tegelijk te berekenen. We starten van een adjacentiematrix adj, die het gewicht bevat van de bogen tussen elk paar toppen. Het gewicht van ontbrekende bogen wordt als oneindig genoteerd. Het algoritme van Floyd gaat dan als volgt:

dist ← adj
for k from 1 to |dist|
   for i from 1 to |dist|
      for j from 1 to |dist|
         if dist[i][j] > dist[i][k] + dist[k][j] 
            dist[i][j] ← dist[i][k] + dist[k][j]
         end if

Implementeer dit algoritme. Zorg ervoor dat niet enkel de lengte van de kortste paden berekend wordt, maar dat je ook de paden zelf kan reconstrueren door extra hulpdata op te slaan.

Schrijf hiervoor drie Python-functies:

• floyd(adj: str) geeft de volledige berekende matrix terug.
• floyddist(adj: str, van: int, naar: int) geeft de kortste afstand van van naar naar terug.
• floydpath(adj: str, van: int, naar: int) geeft het kortste pad van van naar naar terug. Indien er meerdere kortste paden zijn, moet het pad met het minste aantal bezochte paden teruggegeven worden.

Alledrie deze functies krijgen de stringvoorstelling van een adjacentiematrix als input.

Voorbeeldinput:

"
- 4 - -
3 - 7 4
- - - 1
5 6 7 -
"

stelt een adjacentiematrix voor die equivalent is aan deze gewogen adjacentielijst:

{
0:[(4,1)],
1:[(3,0),(7,2),(4,3)],
2:[(1,3)],
3:[(5,0),(6,1),(7,2)]
}

en is ook gelijk aan deze graaf:

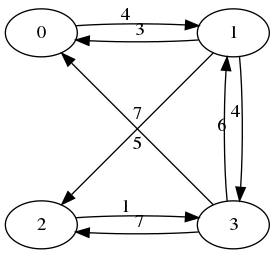
Voorbeeld:

 >>> floyd(open("graaf.in").read())
[[7, 4, 11, 8], [3, 7, 7, 4], [6, 7, 8, 1], [5, 6, 7, 8]]
>>> floyddist(open("graaf.in").read())
8
>>> floydpad(open("graaf.in").read())
[0, 1, 3]

Opmerking

Voor de gegeven doctest moet graaf.in¹ in de huidige directory staan.