Voor een slalomwedstrijd wordt de skipiste opgedeeld in een rechthoekig rooster. Verspreid over dit rooster zijn een aantal poortjes gestoken, waaraan telkens een score wordt toegekend. De rijen van het rooster worden van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf nul. Hierdoor kunnen we een poortje voorstellen als een tuple $$(r, k, s)$$. Daarbij geven het rijnummer $$r$$ en het kolomnummer $$k$$ aan waar het poortje zich bevindt, en geeft $$s \in \mathbb{N}_0$$ de score van het poortje aan.
Een skiër vertrekt bovenaan (boven rij 0 van het rooster) en kan de positie (kolom) waar hij vertrekt vrij kiezen. Bij elke stap verplaatst de skiër zich altijd
-
één rij naar beneden
-
maximaal één kolom naar links of naar rechts
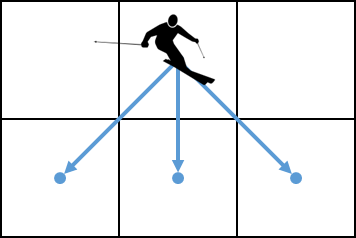
De bewegingsvrijheden van de skiër kunnen dus als volgt weergegeven worden.
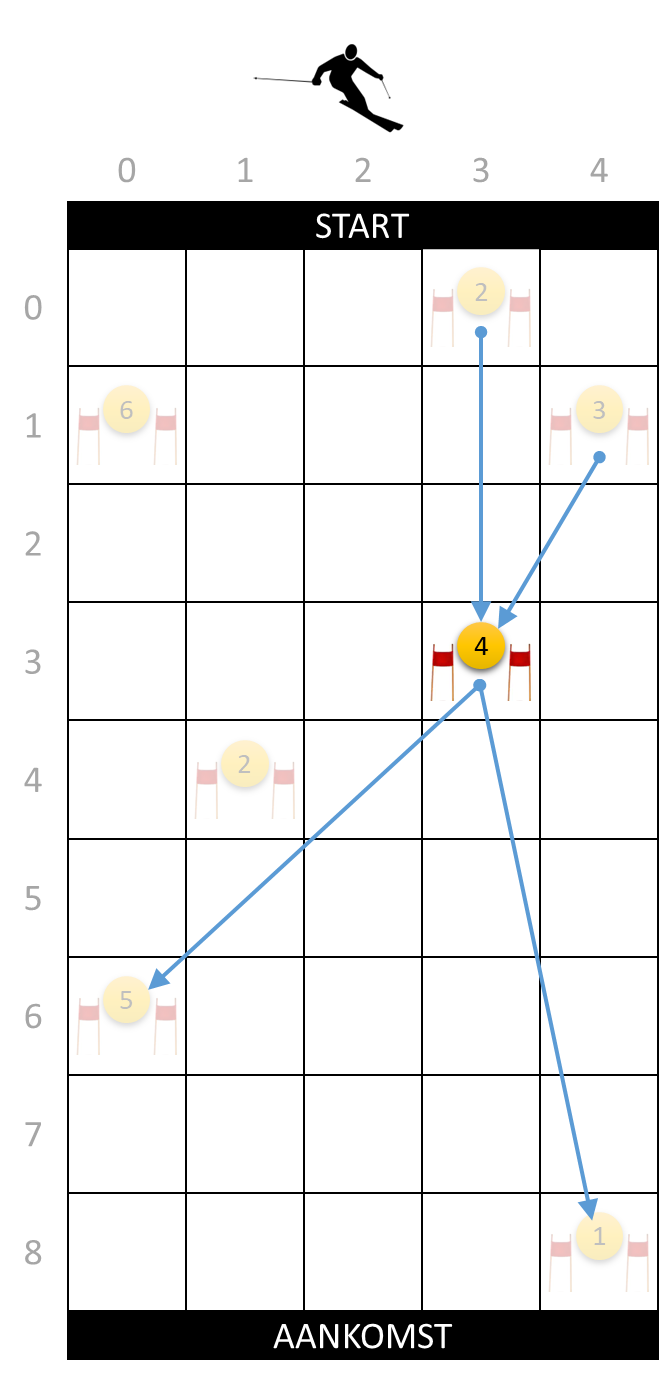
Door zijn beperkte bewegingsvrijheid kan de skiër dus niet altijd een parcours afleggen dat langs alle poortjes van de skipiste loopt. Door zijn vrije keuze van de startpositie is elk poortje wel bereikbaar vanaf de start, maar hij kan niet noodzakelijk van elk poortje naar elk ander poortje skiën. In de linker figuur hieronder zie je bijvoorbeeld dat het poortje op positie $$(3, 3)$$ bereikbaar is vanaf twee hoger gelegen poortjes op posities $$(0, 3)$$ en $$(1, 4)$$, en dat vanaf dit poortje maar twee van de lager gelegen poortjes op posities $$(6, 0)$$ en $$(8, 4)$$ kunnen bereikt worden.
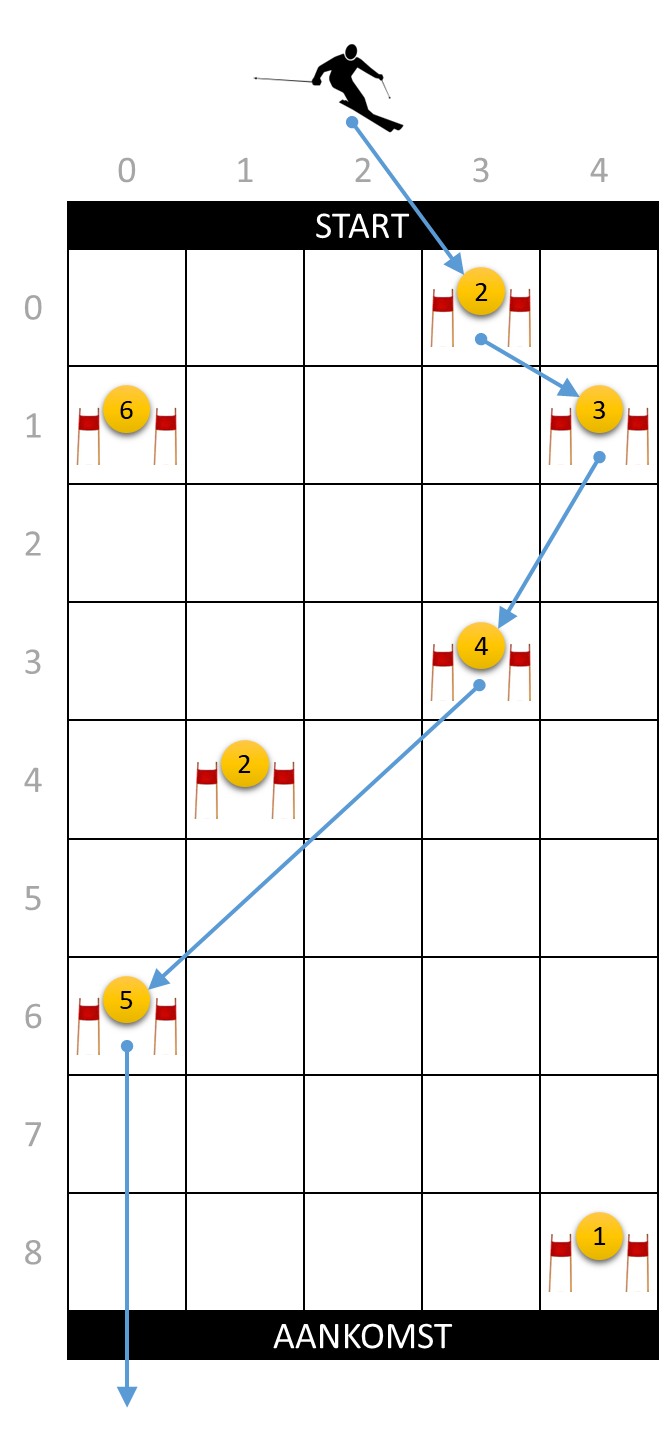
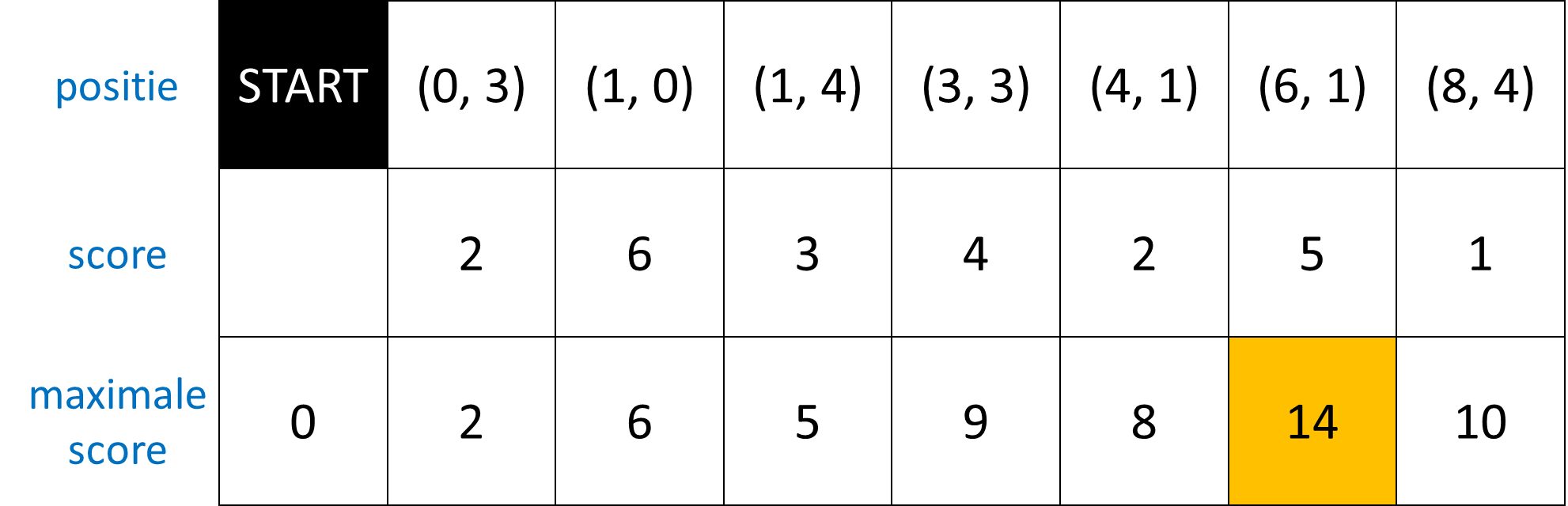
De som van de scores van alle poortjes langs het parcours dat een skiër heeft afgelegd, noemen we de totaalscore van het parcours. Voor een gegeven configuratie van een skipiste kunnen we ons dus afvragen wat de maximale totaalscore is die een skiër kan behalen. Voor de skipiste die we hierboven als voorbeeld gebruikt hebben, is de maximale totaalscore gelijk aan 14. In de rechter figuur hierboven zie je het parcours dat de skiër moet afleggen om die totaalscore te behalen.
Opgave
Het volgende algoritme kan gebruikt worden om de maximale totaalscore te vinden die een skiër op een gegeven skipiste kan behalen:
-
Sorteer de poortjes van boven naar onder en van links naar rechts: $$p_1, p_2, \ldots, p_n$$
-
Bereken de maximale score bij de start en bij elk poortje (in de volgorde zoals bepaald in stap 1).
-
De maximale score bij de start is per definitie gelijk aan nul.
-
De maximale score bij poortje $$p_i$$ is gelijk aan de score van poortje $$p_i$$ plus het maximum van de maximale scores bij de start en bij alle voorgaande poortjes ($$p_1, p_2, \ldots, p_{i-1}$$) waarvan het poortje $$p_i$$ bereikbaar is.
-
-
De maximale totaalscore is gelijk aan het maximum van de maximale scores bij de start en bij alle poortjes.
Hieronder zie je bijvoorbeeld hoe dit algoritme wordt toegepast op de skipiste die we hierboven als voorbeeld gebruikt hebben.
Gevraagd wordt:
-
Schrijf een functie isbereikbaar waaraan de posities van twee poortjes $$p$$ en $$q$$ moeten doorgegeven worden. Hierbij wordt de positie van een poortje voorgesteld als een tuple $$(r, k)$$ met $$r$$ het nummer van de rij en $$k$$ het nummer van de kolom waar het poortje zich in het rooster bevindt. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of $$p$$ bereikbaar is vanaf $$q$$, of omgekeerd.
-
Schrijf een functie max_score_poort waarmee de maximale score bij een poortje kan berekend worden (stap 2 uit het algoritme). Aan de functie moeten twee argumenten doorgegeven worden: i) het poortje waarvoor de maximale score moet berekend worden (een tuple $$(r, k, s)$$) en ii) de maximale scores bij alle voorgaande poortjes. Het tweede argument wordt gegeven als een reeks (list of tuple) van tuples $$(r, k, s_{\text{max}})$$ met het rijnummer $$r$$ en het kolomnummer $$k$$ van een voorgaand poortje, en de maximale score $$s_{\text{max}}$$ bij dat poortje.
-
Schrijf een functie max_totaalscore waaraan een reeks (list of tuple) moet doorgegeven worden met de poortjes op een skipiste. De functie moet de maximale totaalscore teruggeven die een skiër op de gegeven skipiste kan behalen.
Voorbeeld
>>> isbereikbaar((0, 0), (1, 0))
True
>>> isbereikbaar((0, 5), (2, 1))
False
>>> isbereikbaar((0, 0), (3, 3))
True
>>> isbereikbaar((0, 0), (3, 4))
False
>>> max_score_poort((0, 3, 2), [])
2
>>> max_score_poort((1, 0, 6), [(0, 3, 2)])
6
>>> max_score_poort((1, 4, 3), [(1, 0, 6), (0, 3, 2)])
5
>>> max_score_poort((3, 3, 4), [(1, 4, 5), (0, 3, 2), (1, 0, 6)])
9
>>> max_score_poort((4, 1, 2), [(0, 3, 2), (1, 0, 6), (3, 3, 9), (1, 4, 5)])
8
>>> max_score_poort((6, 1, 5), [(3, 3, 9), (1, 4, 5), (0, 3, 2), (1, 0, 6), (4, 1, 8)])
14
>>> max_score_poort((8, 4, 1), [(6, 1, 14), (4, 1, 8), (1, 0, 6), (1, 4, 5), (3, 3, 9), (0, 3, 2)])
10
>>> max_totaalscore([(1, 0, 6), (4, 1, 2), (1, 4, 3), (0, 3, 2), (6, 1, 5), (3, 3, 4), (8, 4, 1)])
14
>>> max_totaalscore([(0, 1, 1), (2, 0, 2), (3, 2, 4)])
5