Piet Mondriaan was een Nederlandse schilder die beschouwd wordt als een van de grote kunstenaars van de 20e eeuw. Sommige van Mondriaans kunstwerken hebben een unieke, geometrische stijl.

Bij een Mondriaanse kunstpuzzel moet je een vierkant $$n \times n$$ rooster ($$n$$ rijen en $$n$$ kolommen) betegelen met niet-overlappende rechthoeken die elk een aantal vakjes van het rooster bedekken.

De afmetingen van een $$h \times b$$ rechthoek worden beschreven met twee natuurlijke getallen: het aantal rijen $$h$$ en het aantal kolommen $$b$$ van het rooster die door de rechthoek bedekt worden. De oppervlakte van een $$h \times b$$ rechthoek is gelijk aan het aantal bedekte vakjes: $$h \times b$$. Het is niet toegelaten om twee rechthoeken met dezelfde afmetingen te gebruiken: als je een deel van het rooster bedekt met een $$h \times b$$ rechthoek, dan mag de betegeling geen andere $$h \times b$$ of $$b \times h$$ rechthoeken meer gebruiken. Een betegeling mag wel twee rechthoeken met dezelfde oppervlakte hebben.

De score van een betegeling is gelijk aan de oppervlakte van de grootste rechthoek min de oppervlakte van de kleinste rechthoek. Het doel is om een betegeling te vinden met een zo klein mogelijke score.

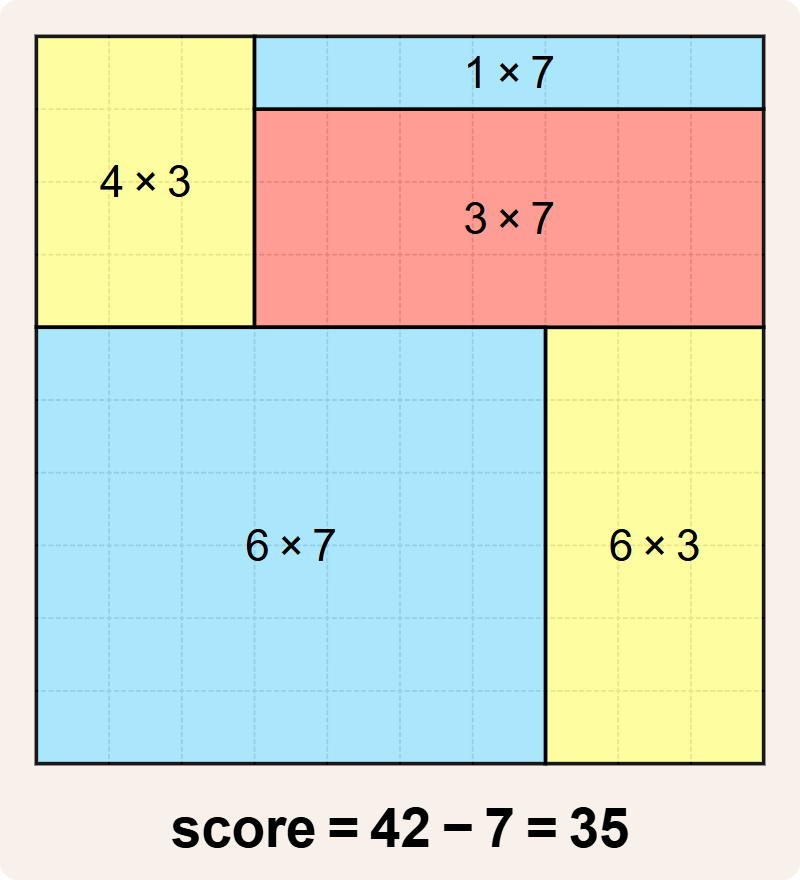
Dit is bijvoorbeeld een betegeling van een $$10 \times 10$$ rooster met score $$42 - 7 = 35$$.

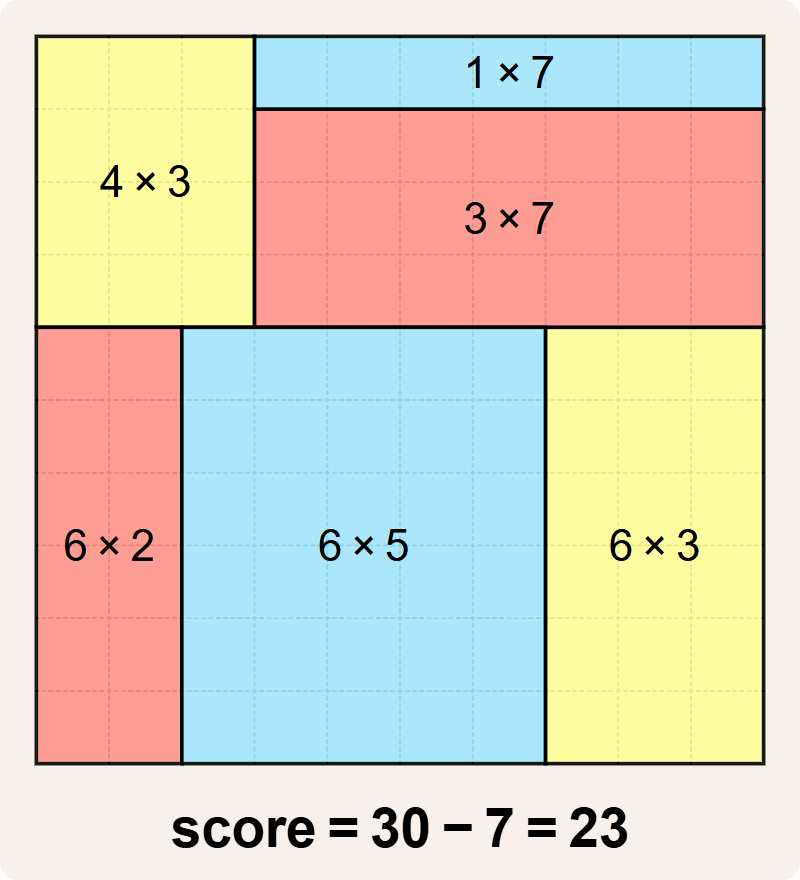
Er zijn echter betere betegelingen mogelijk. Dit is bijvoorbeeld een betegeling met score $$30 - 7 = 23$$. Dat is nog steeds suboptimaal, maar al beter dan wat we hadden.

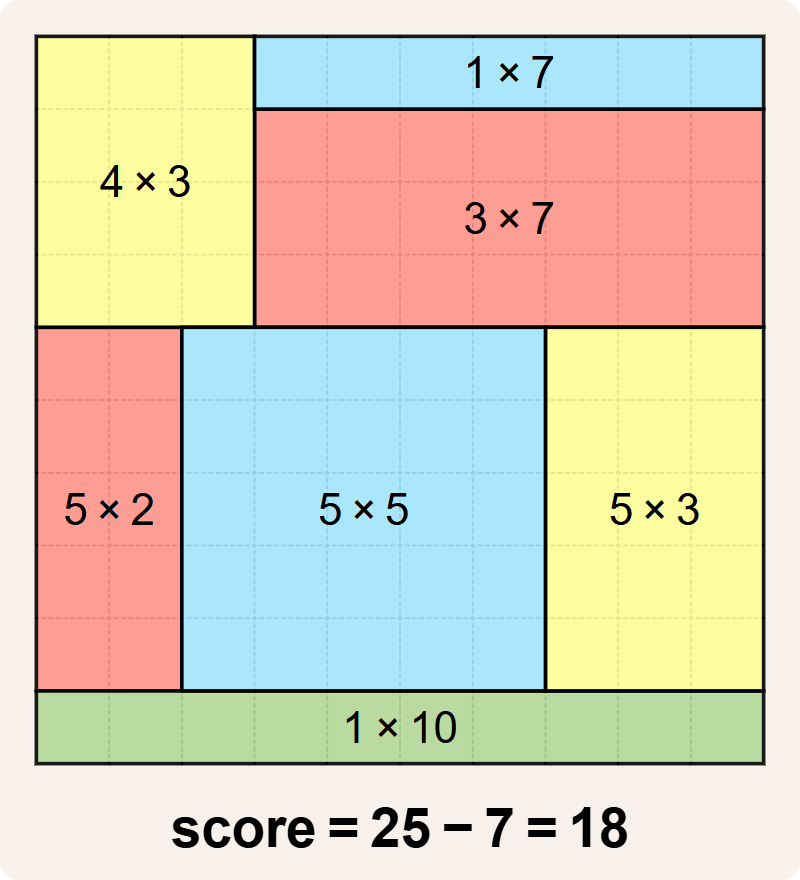
Merk op dat de $$4 \times 3$$ rechthoek en de $$6 \times 2$$ rechthoek weliswaar dezelfde oppervlakte hebben ($$12$$), maar dit is een geldige betegeling omdat ze verschillende afmetingen hebben. Er is echter nog een betere betegeling met score $$25 - 7 = 18$$.

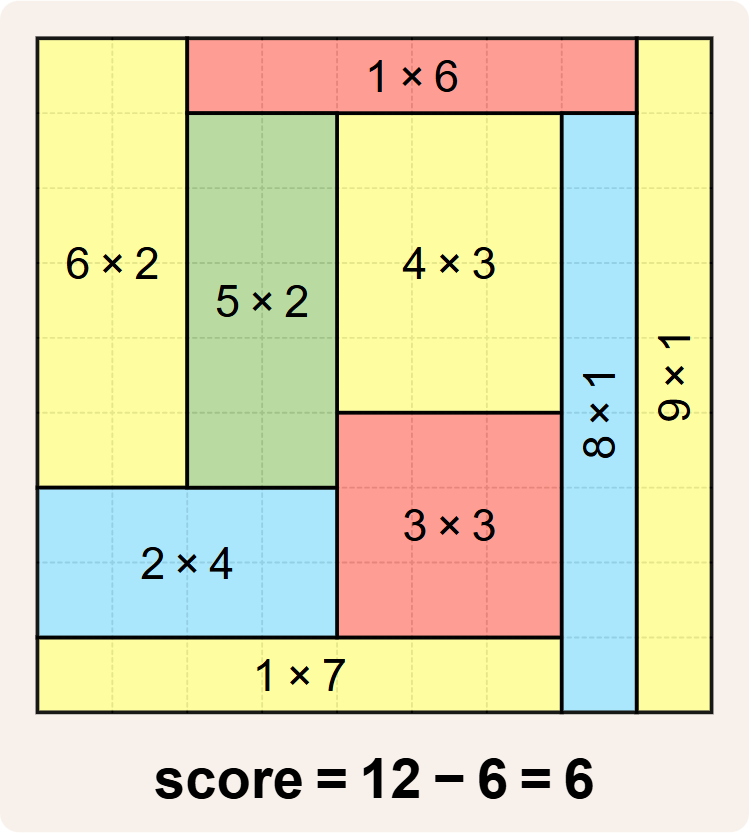
Onderstaande betegeling lijkt de beste die we tot nu toe gevonden hebben, maar dat is ze niet. Ze voldoet immers niet aan de regel dat een betegeling geen rechthoeken met dezelfde afmetingen mag hebben. De betegeling heeft een $$4 \times 3$$ rechthoek en een $$3 \times 4$$ rechthoek, en dat is niet toegelaten. De $$5 \times 2$$ rechthoek en de $$1 \times 10$$ rechthoek hebben dezelfde oppervlakte ($$10$$), maar omdat ze verschillende afmetingen hebben is dat geen inbreuk tegen de regels voor betegelingen.

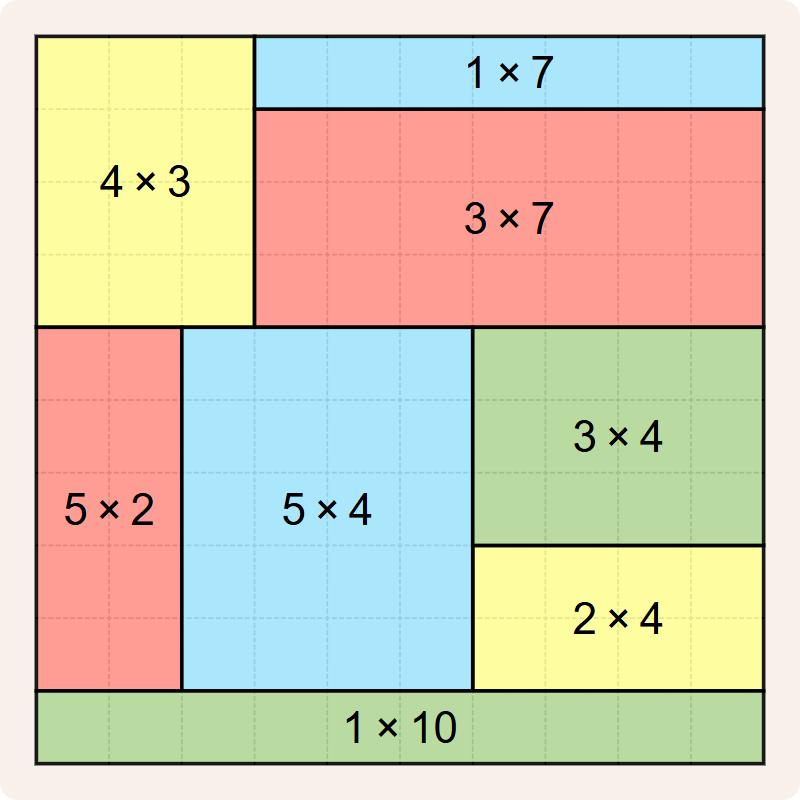
Als bonus hebben we alle rechthoeken ingekleurd met zo weinig mogelijk kleuren, zodat twee rechthoeken met dezelfde kleur nooit een gemeenschappelijk zijde of een gemeenschappelijk hoekpunt hebben.

Opgave

Definieer een klasse Mondriaan waarmee we vierkante $$n \times n$$ roosters ($$n$$ rijen en $$n$$ kolommen) kunnen betegelen volgens de regels van een Mondriaanse kunstpuzzel. Bij het aanmaken van een nieuwe betegeling (Mondriaan) moet de dimensie $$n$$ (int) van het rooster doorgegeven worden.

Om naar de vakjes in het rooster te kunnen verwijzen, nummeren we de rijen van het rooster van boven naar onder en de kolommen van links naar rechts, telkens vanaf nul. Op die manier kunnen we de positie van een vakje voorstellen als een tuple $$(r, k)$$, met $$r$$ het nummer van de rij ($$0 \leq r < n$$) en $$k$$ het nummer van de kolom ($$0 \leq k < n$$) waarop het vakje gelegen is in het rooster.

Het moet mogelijk zijn om rechthoeken toe te voegen aan en te verwijderen uit een betegeling. Bij het toevoegen van een rechthoek aan een betegeling, wordt die rechthoek aangeduid met de eerste niet-gebruikte hoofdletter van het alfabet. Op een betegeling $$\mathcal{M}$$ (Mondriaan) moet je minstens de volgende methoden kunnen aanroepen:

• Een methode volgende_letter waaraan geen argumenten moeten doorgegeven worden. De methode moet de eerste hoofdletter (str) van het alfabet teruggeven die geen rechthoek aanduidt in betegeling $$\mathcal{M}$$.

• Een methode vakjes waaraan vier argumenten moeten doorgegeven worden: i) een rijnummer $$r$$ (int; parameter rij), ii) een kolomnummer $$k$$ (int; parameter kolom), iii) een hoogte $$h$$ (int; parameter hoogte), en iv) een breedte $$b$$ (int; parameter breedte). Deze argumenten beschrijven een $$h \times b$$ rechthoek die met zijn linkerbovenhoek het vakje op rij $$r$$ en kolom $$k$$ in het rooster van betegeling $$\mathcal{M}$$ zou bedekken. Als de rechthoek niet volledig binnen het rooster van betegeling $$\mathcal{M}$$ ligt, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige rechthoek. Anders moet de methode een verzameling (set) teruggeven met de posities (tuple) van alle vakjes in het rooster van betegeling $$\mathcal{M}$$ die door de rechthoek zouden bedekt worden.

• Een methode rechthoek_toevoegen waaraan vier argumenten moeten doorgegeven worden: i) een rijnummer $$r$$ (int; parameter rij), ii) een kolomnummer $$k$$ (int; parameter kolom), iii) een hoogte $$h$$ (int; parameter hoogte), en iv) een breedte $$b$$ (int; parameter breedte). Deze argumenten beschrijven een $$h \times b$$ rechthoek die met zijn linkerbovenhoek het vakje op rij $$r$$ en kolom $$k$$ in het rooster van betegeling $$\mathcal{M}$$ bedekt. Voor deze rechthoek moet gelden dat:

  • de rechthoek ligt volledig binnen het rooster van betegeling $$\mathcal{M}$$

  • betegeling $$\mathcal{M}$$ heeft geen andere rechthoek met dezelfde afmetingen (geen $$h \times b$$ rechthoek en ook geen $$b \times h$$ rechthoek)

  • de rechthoek overlapt niet met een andere rechthoek in betegeling $$\mathcal{M}$$

  Als minstens één van deze voorwaarden niet voldaan is, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige rechthoek en mag er geen rechthoek toegevoegd worden aan betegeling $$\mathcal{M}$$. Anders moet de rechthoek toegevoegd worden aan betegeling $$\mathcal{M}$$ (aangeduid met de eerste hoofdletter van het alfabet die niet is toegekend aan een rechthoek in betegeling $$\mathcal{M}$$) en moet de methode een verwijzing teruggeven naar betegeling $$\mathcal{M}$$.

• Een methode rechthoek_verwijderen waaraan een hoofdletter $$R$$ (str) moet doorgegeven worden. Als hoofdletter $$R$$ geen rechthoek aanduidt in betegeling $$\mathcal{M}$$, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige rechthoek en mag er geen rechthoek verwijderd worden uit betegeling $$\mathcal{M}$$. Anders moet de rechthoek aangeduid met hoofdletter $$R$$ verwijderd worden uit betegeling $$\mathcal{M}$$, en moet de methode een verwijzing teruggeven naar betegeling $$\mathcal{M}$$. Bij het verwijderen van een rechthoek uit betegeling $$\mathcal{M}$$, komt de hoofdletter waarmee de rechthoek aangeduid werd terug vrij om een nieuwe rechthoek aan te duiden die later aan $$\mathcal{M}$$ toegevoegd wordt.

• Een methode bedekking waaraan geen argumenten moeten doorgegeven worden. De methode moet de bedekkingsgraad (int) van betegeling $$\mathcal{M}$$ teruggeven: het aantal vakjes in het rooster die door een rechthoek bedekt worden.

• Een methode score waaraan geen argumenten moeten doorgegeven worden. De methode moet de score (int) van betegeling $$\mathcal{M}$$ teruggeven. Als betegeling $$\mathcal{M}$$ niet alle vakjes in het rooster bedekt, dan is de score per definitie gelijk aan -1.

Als er een betegeling $$\mathcal{M}$$ (Mondriaan) wordt doorgegeven aan de ingebouwde functie str, dan moet die een stringvoorstelling (str) van het rooster van betegeling $$\mathcal{M}$$ teruggeven. Daarin is elke rij van het rooster een afzonderlijke regel, en wordt elk vakje op de rij voorgesteld door de hoofdletter waarmee de rechthoek die het vakje bedekt wordt aangeduid in betegeling $$\mathcal{M}$$, of een onderstrepingsteken (_) als het vakje niet door een rechthoek bedekt wordt in betegeling $$\mathcal{M}$$.

Voorbeeld

In deze interactieve sessie gebruiken we de optimale betegeling van een $$10 \times 10$$ rooster met score 18 uit de inleiding als voorbeeld om te illustreren hoe de klasse Mondriaan moet kunnen gebruikt worden.

>>> puzzel = Mondriaan(10)
>>> print(puzzel)
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
>>> puzzel.bedekking()
0
>>> puzzel.score()
-1
>>> puzzel.volgende_letter()
'A'
>>> puzzel.vakjes(rij=4, kolom=0, hoogte=5, breedte=2)
{(4, 0), (4, 1), (5, 0), (5, 1), (6, 0), (6, 1), (7, 0), (7, 1), (8, 0), (8, 1)}
>>> print(puzzel.rechthoek_toevoegen(rij=4, kolom=0, hoogte=5, breedte=2))
__________
__________
__________
__________
AA________
AA________
AA________
AA________
AA________
__________
>>> puzzel.bedekking()
10
>>> puzzel.score()
-1
>>> puzzel.volgende_letter()
'B'
>>> puzzel.vakjes(rij=1, kolom=3, hoogte=3, breedte=7)
{(1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9), (2, 3), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (2, 9), (3, 3), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (3, 9)}
>>> print(puzzel.rechthoek_toevoegen(rij=1, kolom=3, hoogte=3, breedte=7))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA________
AA________
AA________
__________
>>> puzzel.bedekking()
31
>>> puzzel.score()
-1
>>> puzzel.vakjes(rij=8, kolom=8, hoogte=3, breedte=3)                # rechthoek niet ingesloten in vierkant
Traceback (most recent call last):
AssertionError: ongeldige rechthoek
>>> puzzel.rechthoek_toevoegen(rij=8, kolom=8, hoogte=3, breedte=3)   # rechthoek niet ingesloten in vierkant
Traceback (most recent call last):
AssertionError: ongeldige rechthoek
>>> puzzel.rechthoek_toevoegen(rij=5, kolom=4, hoogte=2, breedte=5)   # andere rechthoek heeft dezelfde afmetingen
Traceback (most recent call last):
AssertionError: ongeldige rechthoek
>>> puzzel.rechthoek_toevoegen(rij=2, kolom=1, hoogte=3, breedte=3)   # rechthoek overlapt met andere rechthoek
Traceback (most recent call last):
AssertionError: ongeldige rechthoek
>>> print(puzzel)
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA________
AA________
AA________
__________
>>> puzzel.volgende_letter()
'C'
>>> print(puzzel.rechthoek_toevoegen(rij=6, kolom=7, hoogte=3, breedte=3))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA_____CCC
AA_____CCC
AA_____CCC
__________
>>> puzzel.volgende_letter()
'D'
>>> print(puzzel.rechthoek_toevoegen(rij=9, kolom=0, hoogte=1, breedte=10))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA_____CCC
AA_____CCC
AA_____CCC
DDDDDDDDDD
>>> puzzel.rechthoek_verwijderen('X')
Traceback (most recent call last):
AssertionError: ongeldige rechthoek
>>> puzzel.volgende_letter()
'E'
>>> print(puzzel.rechthoek_verwijderen('C'))
__________
___BBBBBBB
___BBBBBBB
___BBBBBBB
AA________
AA________
AA________
AA________
AA________
DDDDDDDDDD
>>> puzzel.volgende_letter()
'C'
>>> print(puzzel.rechthoek_toevoegen(rij=0, kolom=0, hoogte=4, breedte=3))
CCC_______
CCCBBBBBBB
CCCBBBBBBB
CCCBBBBBBB
AA________
AA________
AA________
AA________
AA________
DDDDDDDDDD
>>> puzzel.bedekking()
53
>>> puzzel.score()
-1
>>> print(puzzel.rechthoek_toevoegen(0, 3, 1, 7).rechthoek_toevoegen(4, 7, 5, 3).rechthoek_toevoegen(4, 2, 5, 5))
CCCEEEEEEE
CCCBBBBBBB
CCCBBBBBBB
CCCBBBBBBB
AAGGGGGFFF
AAGGGGGFFF
AAGGGGGFFF
AAGGGGGFFF
AAGGGGGFFF
DDDDDDDDDD
>>> puzzel.bedekking()
100
>>> puzzel.score()
18

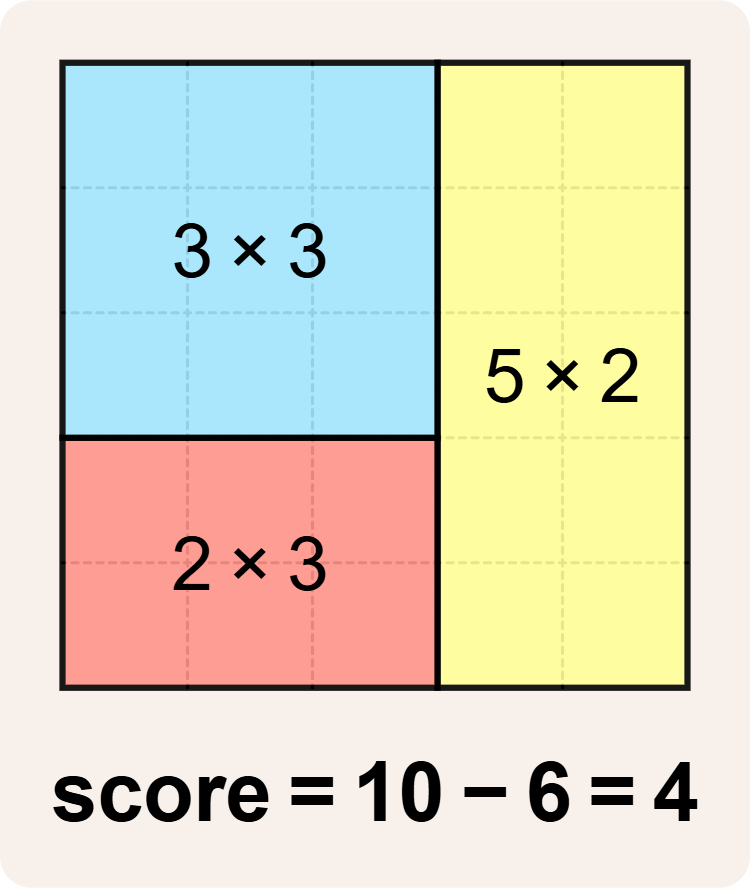
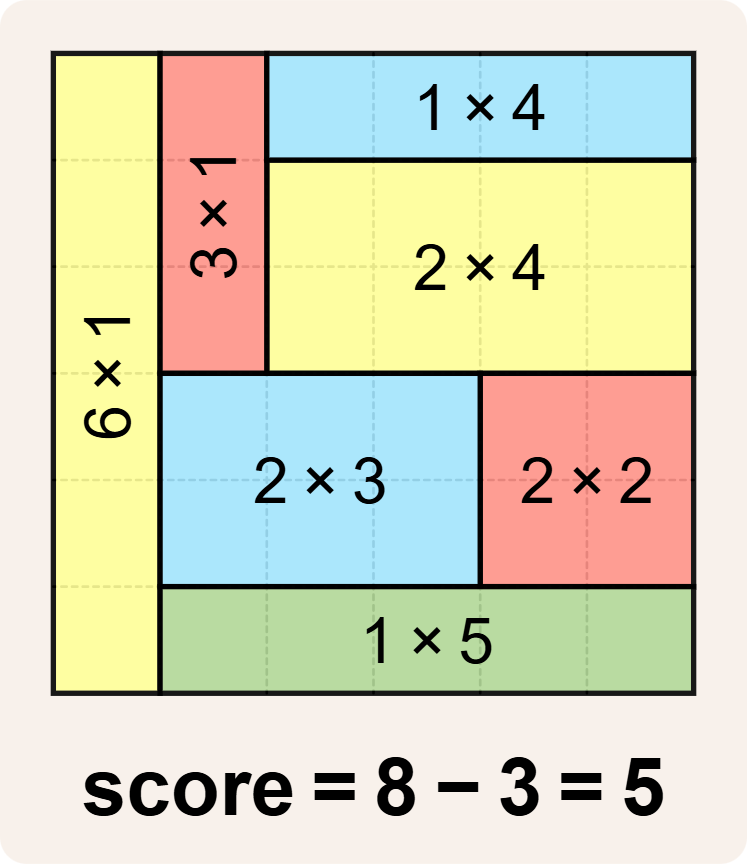
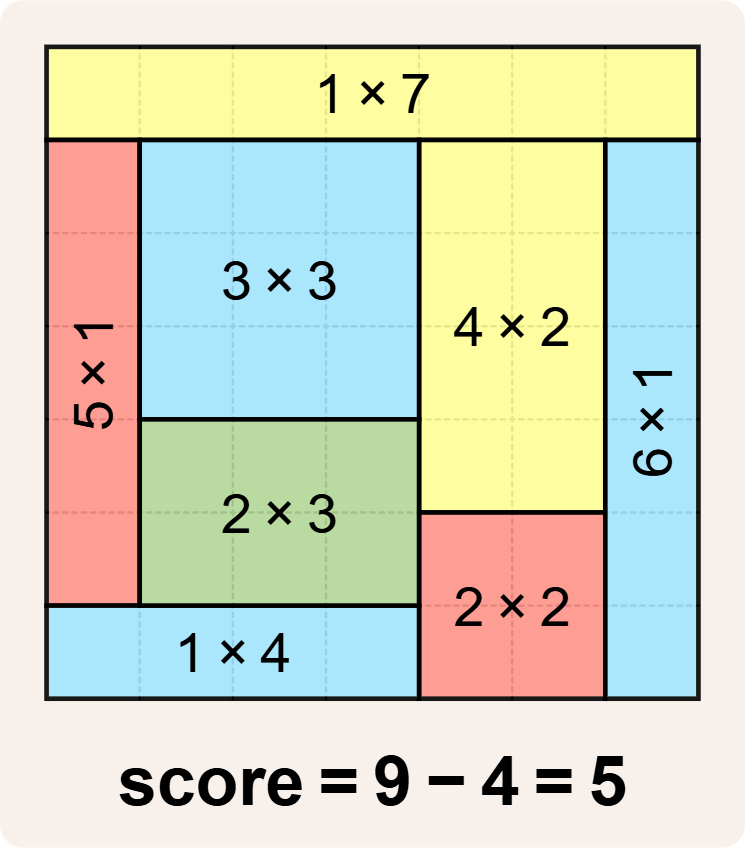
De oplossingen die je indient, worden ook getest aan de hand van deze betegelingen.