DNA bestaat uit vier verschillende basen, die voorgesteld worden door de hoofdletters A, C, G en T. Biologisch gezien hebben deze basen een specifieke betekenis: binnen het coderende deel van een gen coderen drie opeenvolgende basen voor een aminozuur.

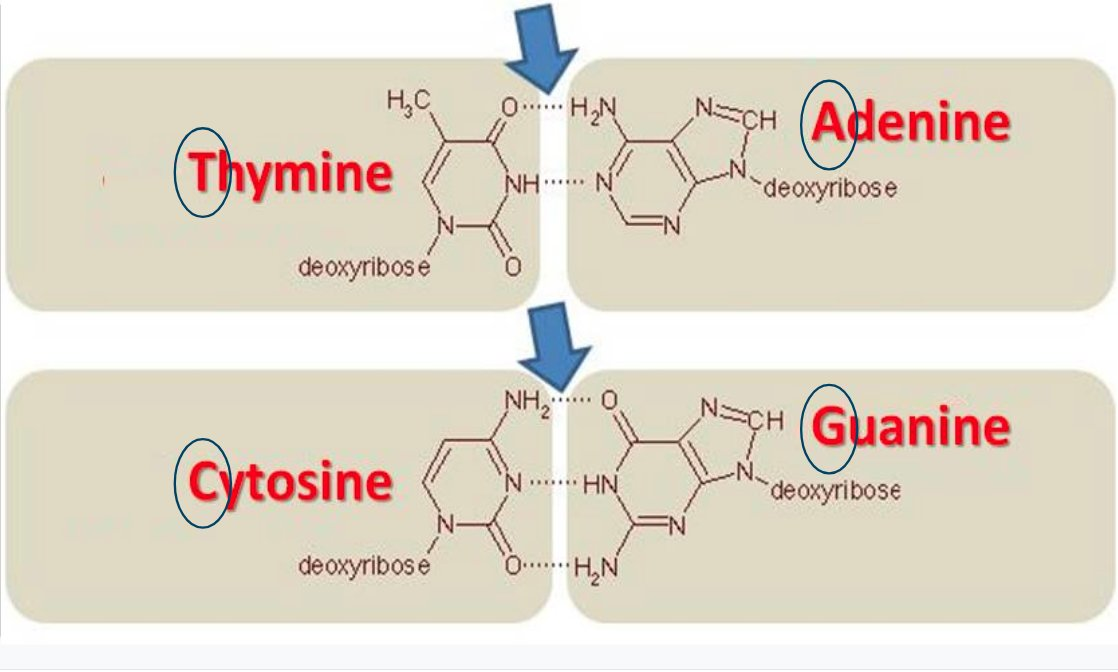
Het meeste DNA wordt redundant opgeslagen in twee met elkaar verbonden strengen. Overal waar er een A staat op de ene streng, vind je een T op de andere streng (en omgekeerd). Op dezelfde manier zijn ook C en G complementair met elkaar.

T G T C A G T
A C A G T C A

Merk ook op hoe de letters van één van de twee strengen doorgaans ondersteboven getekend worden: dat is belangrijk! De ene streng wordt immers van links naar rechts uitgelezen, en de andere van rechts naar links. Als we een DNA-streng hebben, dan is de andere streng het omgekeerd complement¹ dat we bekomen door de DNA-streng om te keren en daarna elke base te vervangen door zijn complement (A door T en vice versa, en C door G en vice versa).

Als je al het DNA van een organisme neemt (beide strengen), dan zal dat evenveel A's en T's bevatten, en ook evenveel C's en G's. Dat is per definitie zo door de complementariteit van de basen tussen de twee strengen, en wordt de eerste pariteitsregel van Chargaff² genoemd.

Vreemd genoeg geldt deze regel ook voor één afzonderlijke DNA-streng. Dus zelfs als je de redundantie weghaalt, dan krijg je per DNA-streng nog altijd ongeveer een gelijk aantal A/T en G/C. Dit wordt de tweede pariteitsregel van Chargaff³ genoemd.

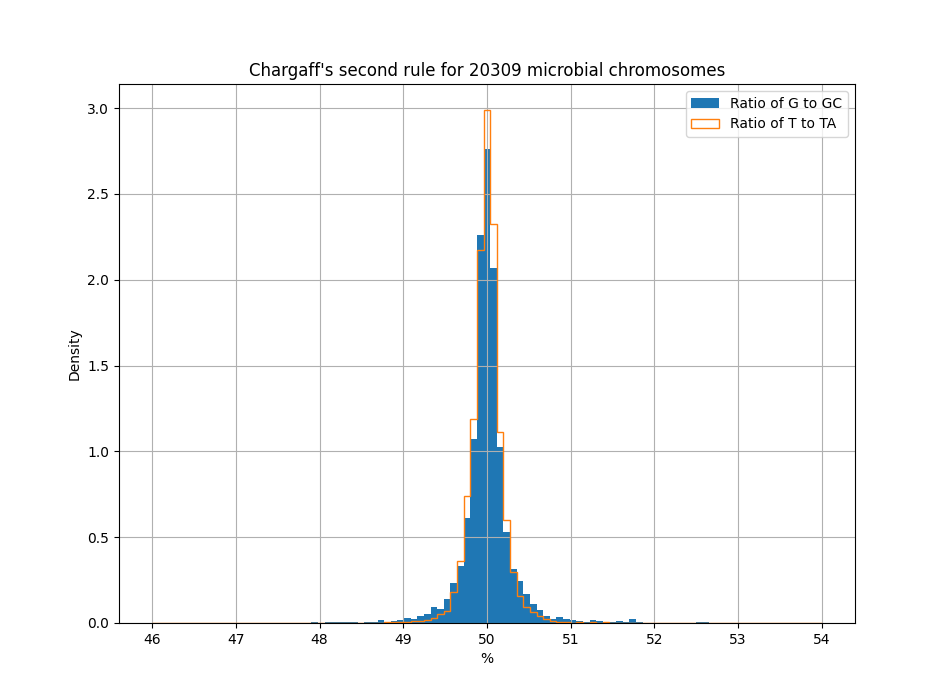
Wetenschappers hebben verschillende theorieën aangevoerd om te verklaren waarom een DNA-streng ongeveer evenveel complementaire basen heeft — de ene al geavanceerder dan de andere⁴ — maar eigenlijk moeten we toegeven dat we op dit moment niet zo goed weten waarom dat zo is. Maar hou je vast, want het wordt nog vreemder.

Deze regel blijkt ook te gelden voor zogenaamde $$k$$-meren, zolang we het aantal voorkomens van een $$k$$-mer vergelijken met zijn omgekeerd complement. Een $$k$$-mer is niets anders dan $$k$$ opeenvolgende basen in een DNA-streng. Voor $$k > 1$$ overlappen opeenvolgende $$k$$-meren met elkaar. Een DNA-streng ACGCTAG heeft bijvoorbeeld zes 2-meren (AC, CG, GC, CT, TA en AG) en vijf 3-meren (ACG, CGC, GCT, CTA en TAG). Voor $$k=1$$ zegt de regel dus dat er ongeveer evenveel C's als G's zijn. Voor $$k=2$$ zijn er bijvoorbeeld ongeveer evenveel CC's als GG's, ongeveer evenveel AG's als CT's (omgekeerd complement), enzoverder.

Voor DNA-tripletten ($$k=3$$) zoals AAA ziet de analyse er bijvoorbeeld uit zoals in onderstaande grafiek. Daarbij zetten we telkens het aantal voorkomens van twee complementaire tripletten naast elkaar. Aan de linkerkant staat een blauwe balk die bijvoorbeeld het aantal voorkomens van AAA aanduidt en aan de rechterkant een oranje balk die het aantal voorkomens van het omgekeerd complement TTT aanduidt. Dit doen we voor de 32 paren tripletten. De overeenkomst tussen het aantal voorkomens van elk paar is verbluffend:

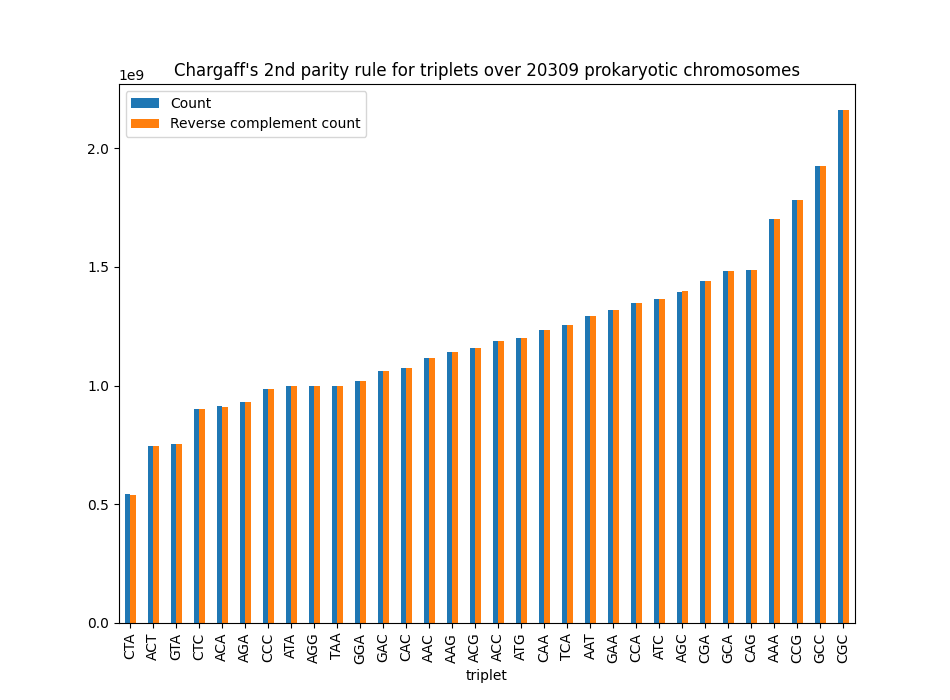
Dus opnieuw: waarom is dat zo? Daarvoor circuleren de wildste theorieën, maar er is bijlange nog geen consensus. En dat maakt het net zo interessant! In de kern van het leven schuilt een mysterie dat we eenvoudig kunnen analyseren aan de hand van een computer. Op die manier hopen we op een dag het mysterie te kunnen ontrafelen.

Opgave

We vragen je om een klasse DNA te definiëren om DNA-strengen voor te stellen, een functie lees_fasta om een DNA-streng uit een FASTA-bestand te lezen, en een klasse Analyse om $$k$$-mer analyses uit te voeren op een DNA-streng.

DNA-strengen

Definieer een klasse DNA waarmee DNA-strengen kunnen voorgesteld worden. Bij het aanmaken van een DNA-streng (DNA) moet een string (str) doorgegeven worden met de opeenvolgende basen van de DNA-streng. Als de string een karakter bevat dat geen A, C, G of T is, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige DNA-streng. DNA-strengen (DNA) zijn onveranderlijk (immutable).

• Als er een DNA-streng (DNA) wordt doorgegeven aan de ingebouwde functie len, dan moet de lengte van de DNA-streng teruggegeven worden. Dit is een getal (int) dat aangeeft hoeveel basen er in de DNA-streng voorkomen.

• Als er een DNA-streng (DNA) wordt doorgegeven aan de ingebouwde functie repr, dan moet een stringvoorstelling (str) teruggegeven worden die leest als een Python-expressie waarmee een nieuwe DNA-streng (DNA) aangemaakt wordt met dezelfde basen als de DNA-streng die aan de functie repr werd doorgegeven.

• Als er een DNA-streng (DNA) wordt doorgegeven aan de ingebouwde functie str, dan moet een string (str) teruggegeven worden met de voorstellingen van de opeenvolgende basen van de DNA-streng.

• Voor twee DNA-strengen $$s_1$$ en $$s_2$$ (DNA) moet de uitdrukking $$s_1 + s_2$$ een nieuwe DNA-streng (DNA) opleveren, met de basen van $$s_1$$ gevolgd door de basen van $$s_2$$.

• DNA-strengen moeten ook een methode omgekeerd_complement hebben, waaraan geen argumenten moeten doorgegeven worden. De methode moet een DNA-streng (DNA) teruggeven waarvan de basen het omgekeerd complement vormen van de DNA-streng waarop de methode wordt aangeroepen.

FASTA-bestanden

Definieer een functie lees_fasta waaraan de locatie (str) van een FASTA-bestand moet doorgegeven worden. De functie moet de DNA-streng (DNA) uit het bestand teruggeven.

>seq
AGCTGCATGACTACGACTAC
TAGTCGGATTAGGCATGCTA
CT

$$k$$-mer analyses

Definieer een klasse Analyse waarmee $$k$$-mer analyses kunnen uitgevoerd worden op een DNA-streng. Bij het aanmaken van een $$k$$-mer analyse (Analyse) moeten twee argumenten doorgegeven worden: i) een DNA-streng $$\delta$$ (DNA) en ii) een getal $$k \in \mathbb{N}_0$$ (int). Een $$k$$-mer analyse (Analysis) moet minstens de volgende methoden ondersteunen:

• Een methode kmeren waaraan geen argumenten moeten doorgegeven worden. De methode moet een lijst (list) teruggeven met de opeenvolgende $$k$$-meren in DNA-streng $$\delta$$. Hierbij worden de $$k$$-meren als strings (str) voorgesteld.

• Een methode aantal waaraan een string $$\kappa$$ (str) moet doorgegeven worden. Als $$\kappa$$ niet bestaat uit $$k$$ letters of als minstens één van die letters geen DNA-base voorstelt (A, C, G of T), dan moet een AssertionError opgeworpen worden met de boodschap ongeldig k-mer. Anders moet de methode een tuple teruggeven met twee getallen (int): i) het aantal keer dat $$k$$-mer $$\kappa$$ voorkomt in DNA-streng $$\delta$$ en ii) het aantal keer dat het omgekeerd complement van $$k$$-mer $$\kappa$$ voorkomt in DNA-streng $$\delta$$.

Voorbeeld

Onderstaande voorbeeldsessie gaat ervan uit dat de FASTA-bestanden seq.fasta⁶ en mitochondrion.fasta⁷ in de huidige directory staan.

>>> dna1 = DNA('AGCTTTTCATTCTGACTGCATGATAGCAGC')
>>> dna1
DNA('AGCTTTTCATTCTGACTGCATGATAGCAGC')
>>> print(dna1)
AGCTTTTCATTCTGACTGCATGATAGCAGC
>>> len(dna1)
30
>>> dna1.omgekeerd_complement()
DNA('GCTGCTATCATGCAGTCAGAATGAAAAGCT')

>>> DNA('XYZ')
Traceback (most recent call last):
AssertionError: ongeldige DNA-streng

>>> dna2 = lees_fasta('seq.fasta8')
>>> dna2
DNA('AGCTGCATGACTACGACTACTAGTCGGATTAGGCATGCTACT')
>>> len(dna2)
42
>>> dna2.omgekeerd_complement()
DNA('AGTAGCATGCCTAATCCGACTAGTAGTCGTAGTCATGCAGCT')

>>> dna3 = dna1 + dna2
>>> dna3
DNA('AGCTTTTCATTCTGACTGCATGATAGCAGCAGCTGCATGACTACGACTACTAGTCGGATTAGGCATGCTACT')
>>> len(dna3)
72

>>> analyse = Analyse(dna1, 2)
>>> analyse.kmeren()
['AG', 'GC', 'CT', 'TT', 'TT', 'TT', 'TC', 'CA', 'AT', 'TT', 'TC', 'CT', 'TG', 'GA', 'AC', 'CT', 'TG', 'GC', 'CA', 'AT', 'TG', 'GA', 'AT', 'TA', 'AG', 'GC', 'CA', 'AG', 'GC']
>>> analyse.aantal('TT')
(4, 0)
>>> analyse.aantal('GA')
(2, 2)
>>> analyse.aantal('ACT')
Traceback (most recent call last):
AssertionError: ongeldig k-mer

>>> mitochondrion = lees_fasta('mitochondrion.fasta9')
>>> len(mitochondrion)
16569
>>> analyse = Analyse(mitochondrion, 3)
>>> analyse.aantal('TT')
Traceback (most recent call last):
AssertionError: ongeldig k-mer
>>> analyse.aantal('GTA')
(154, 377)
>>> analyse.aantal('CTG')
(180, 199)

Bronnen

• Fariselli P, Taccioli C, Pagani L, Maritan A (2021). DNA sequence symmetries from randomness: the origin of the Chargaff's second parity rule. Briefings in bioinformatics 22(2), 2172–2181. ¹⁰