Een schaakbord bestaat uit 64 vierkanten die gerangschikt zijn in een rooster van 8 rijen en 8 kolommen. De vierkanten hebben afwisselend een lichte en een donkere kleur. De rijen van het bord worden van onder naar boven aangeduid met de cijfers 1–8. De kolommen worden van links naar rechts aangeduid met de letters a–h. Op die manier kan elk vierkant op het bord aangeduid worden met de letter van de kolom en het cijfer van de rij waarop het vierkant gelegen is.
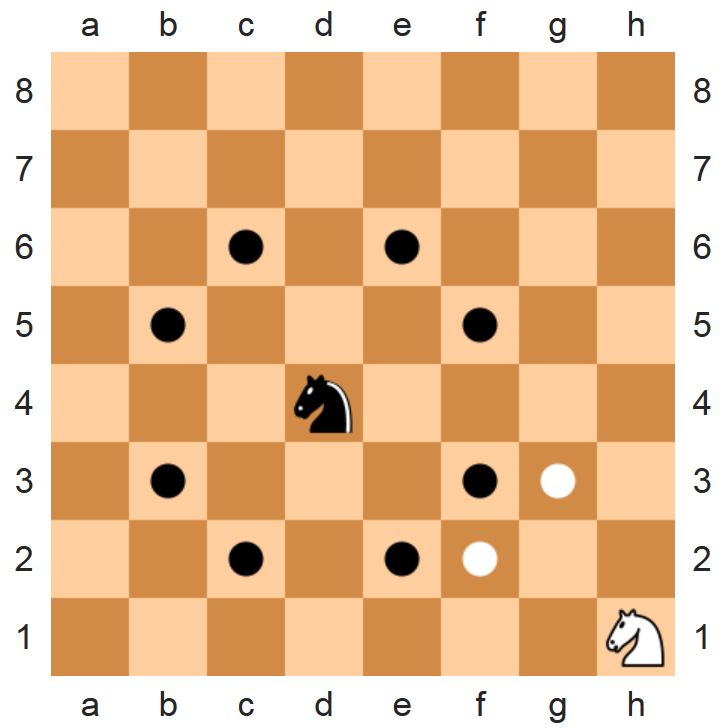
Het paard is één van de zes verschillende stukken van het schaakspel. De manier waarop een paard kan bewegen over het schaakbord — de paardensprong — is ongebruikelijk onder de schaakstukken. Als het paard beweegt, dan verplaatst het zich naar een positie die twee vierkanten horizontaal en één vierkant verticaal, of één vierkant horizontaal en twee vierkanten verticaal verwijderd is van zijn oorspronkelijke positie. Daardoor heeft de volledige beweging van het paard de vorm van de letter L en springt het paard afwisselend naar lichte en donkere vierkanten.
In tegenstelling tot de andere schaakstukken kan een paard over alle andere schaakstukken springen naar een nieuwe positie, ongeacht hun kleur. Het vangt een vijandelijk stuk door het te vervangen op zijn nieuwe positie. Het vermogen van het paard om over andere stukken te springen, betekent dat het meest tot zijn recht komt in ingesloten posities, in tegenstelling tot bijvoorbeeld de loper.
De paardensprong is al meer dan zeven eeuwen een vast onderdeel van het schaakspel, en is daarmee één van de langst overlevende bewegingen in het spel. Daardoor komt het ook voor in de meeste lokale varianten van het schaakspel.
Invoer
Twee regels die elk een vierkant op het schaakbord aanduiden.
Uitvoer
Een regel die aangeeft of het paard van het eerste vierkant naar het tweede vierkant op het schaakbord kan springen. Bekijk onderstaande voorbeelden om te zien in welk formaat de uitvoer moet opgemaakt worden.
Voorbeeld
Invoer:
d4
e6Uitvoer:
het paard kan springen van d4 naar e6Voorbeeld
Invoer:
h1
c2Uitvoer:
het paard kan niet springen van h1 naar c2Epiloog
Het Lo Shu vierkant1 is het $$3 \times 3$$ vierkant dat ingesloten wordt door de stippellijnen in het midden van onderstaand diagram. Het is "magisch": de som van de drie getallen op elke rij, kolom en diagonaal (aangeduid met rode lijnen) is gelijk aan 15.
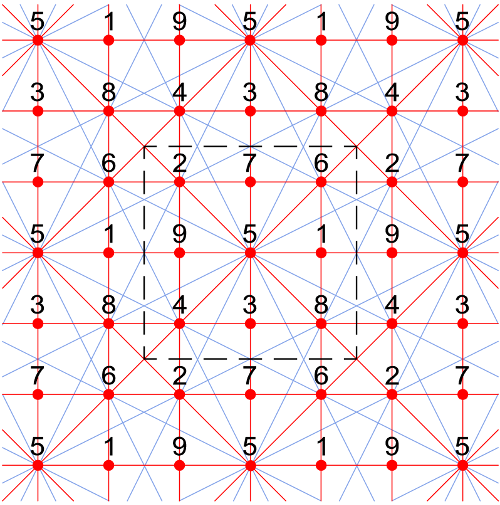
William Walkington heeft een nieuwe magische eigenschap2 ontdekt. Stel je voor dat je een buis betegelt met het vierkant en dat je de buis vervolgens ombuigt tot een torus3. Stel je nu voor dat je op de torus met een paardenspong van cel naar cel springt — twee cellen in één richting en één in een richting loodrecht daarop. Het uitgebreide diagram hierboven helpt je om je dit voor te stellen — volg de blauwe lijnen. Nu blijkt dat de som van drie opeenvolgende cellen op een dergelijk pad ook telkens 15 is. Het vierkant is dus nog magischer dan dat we eerst dachten.