Valknut is een geheimschrift waarbij elk symbool (een letter, een cijfer, een leesteken of een spatie) voorgesteld wordt als een unieke combinatie van twee cijfers (1–9). Omgekeerd correspondeert elk cijferpaar (1–9) met een uniek symbool. Omdat het cijfer nul niet gebruikt wordt, zijn er in totaal 81 verschillende cijferparen en dus ook 81 verschillende symbolen.

Een sleutel voor het valknut-geheimschrift legt voor elk symbool $$\alpha$$ (een letter, een cijfer, een leesteken of een spatie) het corresponderende cijferpaar $$ij$$ ($$1 \leq i, j \leq 9$$) vast. Dat gebeurt in een tekstbestand dat uit 81 regels bestaat. Elke regel bevat één symbool $$\alpha$$, gevolgd door het corresponderende cijfer $$i$$ en het corresponderende cijfer $$j$$, telkens van elkaar gescheiden door een tab. Merk op dat een tab nooit als symbool gebruikt wordt in het valknut-geheimschrift. Een dergelijk bestand kan er bijvoorbeeld als volgt uitzien (valknut.txt¹):

Volgens deze sleutel wordt hoofdletter W bijvoorbeeld voorgesteld als cijferpaar 26, kleine letter e als cijferpaar 63, cijfer 4 als cijferpaar 86, een spatie als cijferpaar 68, en een punt (.) als cijferpaar 27.

Om voor een cijferpaar $$ij$$ ($$1 \leq i, j \leq 9$$) snel het corresponderende symbool $$\alpha$$ te kunnen opzoeken, worden de 81 symbolen van een valknut-sleutel in een $$9 \times 9$$ rooster met 9 rijen en 9 kolommen geplaatst. De rijen van dit rooster worden van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf 1. Het cijferpaar $$ij$$ is dan niets anders dan het rijnummer $$i$$ en het kolomnummer $$j$$ van de cel in het rooster waar het corresponderende symbool $$\alpha$$ kan gevonden worden. Dit is het rooster voor de sleutel die we hierboven als voorbeeld gebruikt hebben:

In de roostervoorstelling van een valknut-sleutel worden de 81 symbolen in een $$9 \times 9$$ rooster met 9 rijen en 9 kolommen geplaatst. De rijen van dit rooster worden van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf 1. Het cijferpaar $$ij$$ is dan niets anders dan het rijnummer $$i$$ en het kolomnummer $$j$$ van de cel in het rooster waar het corresponderende symbool kan gevonden worden.

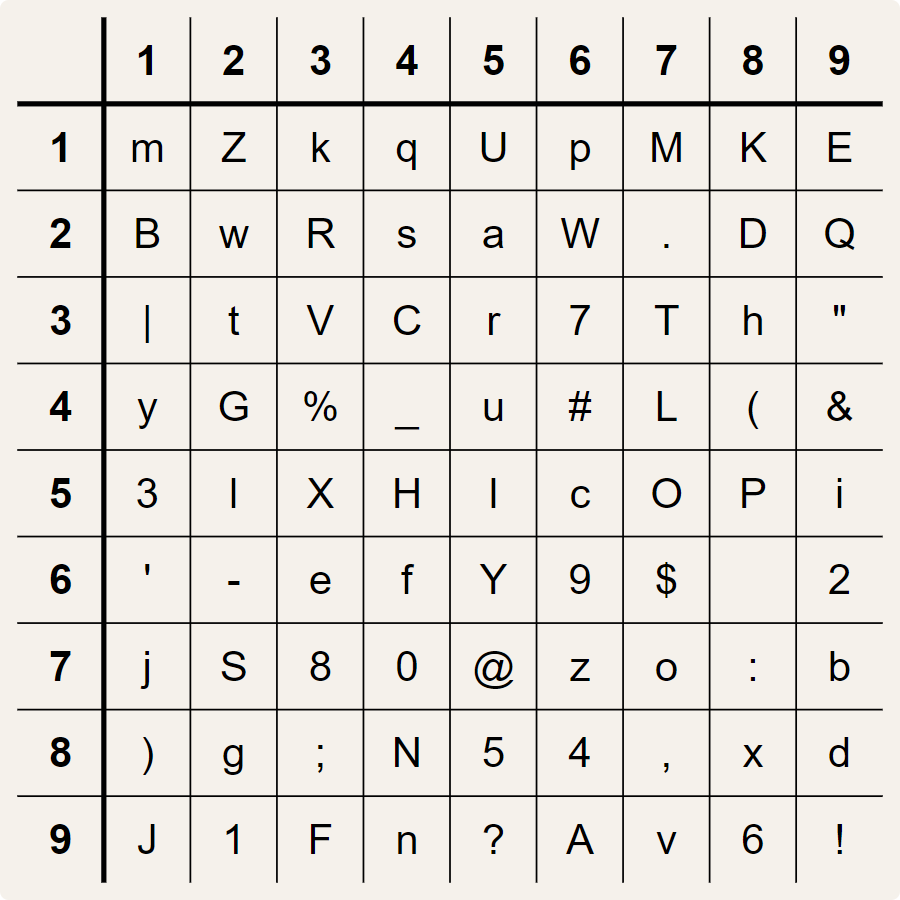
Voor cijferpaar 26 vinden we in dit rooster op rij 2 en kolom 6 de hoofdletter W. Analoog correspondeert cijferpaar 63 met kleine letter e, cijferpaar 86 met cijfer 4, cijferpaar 68 met een spatie (lege cel op rij 6 en kolom 8), en cijferpaar 27 met een punt (.).

Coderen en decoderen

Vikingen zijn vooral gekend als geduchte krijgers die uitblonken in fysieke kracht. Ze waren echter ook bijzonder intelligent en spiritueel aangelegd. Dit is een van hun belangrijke levenslessen:

Where wolf's ears are, wolf's teeth are near.

We gebruiken de sleutel uit de inleiding (valknut.txt²) om te illustreren hoe deze klare tekst gecodeerd wordt volgens het valknut-geheimschrift. Eerst zetten we elk symbool van de klare tekst om naar het corresponderende cijferpaar (W→ 26, h → 38, e → 63, …, . → 27). Als we al deze cijferparen achter elkaar zetten, dan krijgen we de cijferreeks:

263863356368227752646124686325352468253563876822775264612468326363323868253563689463253527

Als we elk cijferpaar van deze reeks zouden omzetten naar het corresponderende symbool, dan krijgen we uiteraard terug de oorspronkelijke klare tekst. Maar eerst wisselen we nog de volgorde van de twee cijfers van elk cijferpaar om. We krijgen dan de cijferreeks:

628336533686227725461642863652534286525336788622772546164286233636238386525336864936525372

Als we nu elk cijferpaar van deze reeks terug omzetten naar het corresponderende symbool, dan krijgen we de cijfertekst:

-;7X74woa#pG47lXG4lX7:4woa#pG4R77R;4lX74&7lXS

Het is heel eenvoudig om deze cijfertekst te decoderen: dat werkt op exact dezelfde manier als het coderen van de klare tekst.

Opgave

Schrijf een functie lees_sleutel waaraan de locatie (str) moet doorgegeven worden van een tekstbestand met een valknut-sleutel $$\mathcal{V}$$. De functie moet de dictionaryvoorstelling van valknut-sleutel $$\mathcal{V}$$ teruggeven: een dictionary (dict) die elk symbool $$\alpha$$ (str) van de sleutel afbeeldt op een tuple $$(i, j)$$, waarbij $$i$$ (int) en $$j$$ (int) samen het cijferpaar $$ij$$ ($$1 \leq i, j \leq 9$$) vormen dat volgens de sleutel correspondeert met symbool $$\alpha$$.
Schrijf een functie symbolen2cijfers waaraan twee argumenten moeten doorgegeven worden: i) een reeks symbolen $$s$$ (str) en ii) de dictionaryvoorstelling (dict) van een valknut-sleutel $$\mathcal{V}$$. De functie mag ervan uitgaan dat alle symbolen van $$s$$ voorkomen in sleutel $$\mathcal{V}$$, zonder dat dit expliciet moet gecontroleerd worden. De functie moet de cijferreeks $$c$$ (str) teruggeven die volgens sleutel $$\mathcal{V}$$ correspondeert met de reeks symbolen $$s$$. De functie heeft ook nog een derde optionele parameter wisselen waaraan een Booleaanse waarde (bool) kan doorgegeven worden (standaardwaarde: False). Als de waarde True wordt doorgegeven aan de parameter wisselen, dan moet elke cijferpaar omgewisseld worden in de cijferreeks $$c$$ die door de functie wordt teruggeven.
Schrijf een functie maak_rooster waaraan de dictionaryvoorstelling (dict) van een valknut-sleutel $$\mathcal{V}$$ moet doorgeven worden. De functie moet de roostervoorstelling van valknut-sleutel $$\mathcal{V}$$ teruggeven: een nieuwe dictionary (dict) die elk van de cijfers 1–9 (int) afbeeldt op een string (str) met de symbolen op de corresponderende rij in de roostervoorstelling van de sleutel (opgelijst van links naar rechts).
Schrijf een functie cijfers2symbolen waaraan twee argumenten moeten doorgegeven worden: i) een cijferreeks $$c$$ (str) en ii) de roostervoorstelling van een valknut-sleutel $$\mathcal{V}$$. De functie mag ervan uitgaan dat reeks $$c$$ bestaat uit een even aantal cijfers 1–9, zonder dat dit expliciet moet gecontroleerd worden. De functie moet de reeks symbolen $$s$$ (str) teruggeven die volgens sleutel $$\mathcal{V}$$ correspondeert met cijferreeks $$c$$. De functie heeft ook nog een derde optionele parameter wisselen waaraan een Booleaanse waarde (bool) kan doorgegeven worden (standaardwaarde: False). Als de waarde True wordt doorgegeven aan de parameter wisselen, dan moet elke cijferpaar in cijferreeks $$c$$ eerst omgewisseld worden, voordat de functie het corresponderende symbool voor reeks $$s$$ bepaalt.
Schrijf een functie codeer waaraan twee argumenten moeten doorgegeven worden: i) een klare tekst $$t$$ (str) en ii) de dictionaryvoorstelling (dict) van een valknut-sleutel $$\mathcal{V}$$. De functie moet de cijfertekst (str) teruggeven die men bekomt door klare tekst $$t$$ te coderen volgens het valknut-geheimschrift met sleutel $$\mathcal{V}$$.
Schrijf een functie decodeer waaraan twee argumenten moeten doorgegeven worden: i) een cijfertekst (str) die bekomen werd door een klare tekst $$t$$ te coderen volgens het valknut-geheimschrift en ii) de dictionaryvoorstelling (dict) van de valknut-sleutel $$\mathcal{V}$$ die bij het coderen gebruikt werd. De functie moet klare tekst $$t$$ teruggeven.

Voorbeeld

In onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand valknut.txt³ zich in de huidige directory bevindt.

        >>> sleutel = lees_sleutel('valknut.txt4')
>>> sleutel['W']
(2, 6)
>>> sleutel['h']
(3, 8)
>>> sleutel[' ']
(6, 8)
>>> sleutel['.']
(2, 7)

>>> symbolen2cijfers("Where wolf's ears are, wolf's teeth are near.", sleutel)
'263863356368227752646124686325352468253563876822775264612468326363323868253563689463253527'
>>> symbolen2cijfers("Where wolf's ears are, wolf's teeth are near.", sleutel, wisselen=True)
'628336533686227725461642863652534286525336788622772546164286233636238386525336864936525372'

>>> rooster = maak_rooster(sleutel)
>>> rooster
{1: 'mZkqUpMKE', 2: 'BwRsaW.DQ', 3: '|tVCr7Th"', 4: 'yG%_u#L(&', 5: '3lXHIcOPi', 6: "'-efY9$ 2", 7: 'jS80@zo:b', 8: ')g;N54,xd', 9: 'J1Fn?Av6!'}

>>> cijfers2symbolen('263863356368227752646124686325352468253563876822775264612468326363323868253563689463253527', rooster)
"Where wolf's ears are, wolf's teeth are near."
>>> cijfers2symbolen('628336533686227725461642863652534286525336788622772546164286233636238386525336864936525372', rooster, wisselen=True)
"Where wolf's ears are, wolf's teeth are near."

>>> codeer("Where wolf's ears are, wolf's teeth are near.", sleutel)
'-;7X74woa#pG47lXG4lX7:4woa#pG4R77R;4lX74&7lXS'

>>> decodeer('-;7X74woa#pG47lXG4lX7:4woa#pG4R77R;4lX74&7lXS', sleutel)
"Where wolf's ears are, wolf's teeth are near."

Epiloog

Het valknut-geheimschrift dankt haar naam aan de vorm waarin de sleutel van het geheimschrift normaal gezien weergegeven wordt. De valknut (Oudnoords; valr: gesneuvelde krijgers + knut: knoop) is een symbool dat bestaat uit drie in elkaar gestrengelde driehoeken. Het staat op oude Germaanse artefacten gegraveerd, meestal samen met verwijzingen naar de god Odin⁵. Daarom wordt het ook wel de Odins- of Wodansknoop genoemd. De valknut werd teruggevonden in Gotland⁶ op de 8e-eeuwse Steen van Tängelgarda⁷ en de Steen van Stora Hammar⁸. Maar ook op een ring die gevonden werd in de Engelse rivier Nene⁹ en op het Oseberg vikingschip¹⁰ dat je in het Noorse Vikingskipshuset museum¹¹ kunt bezichtigen.

De valknut (Oudnoords; valr: gesneuvelde krijgers + knut: knoop) is een symbool dat bestaat uit drie in elkaar gestrengelde driehoeken. Het staat op oude Germaanse artefacten gegraveerd, meestal samen met verwijzingen naar de god Odin. Daarom wordt het ook wel de Odins- of Wodansknoop genoemd.

De valknut-voorstelling van een sleutel heeft in het midden een driehoek met daarin de negen cijfers 1–9. Daarrond staan drie trapezia met daarin de 81 symbolen. Elk trapezium bestaat zelf uit drie driehoeken met daarin telkens negen symbolen, goed voor 27 symbolen per trapezium.

Een sleutel van het valknut-geheimschrift wordt voorgesteld in de vorm van het gelijknamige symbool. In het midden staat een driehoek met daarin de negen cijfers 1–9. Daarrond staan drie trapezia met daarin 81 symbolen (letters, cijfers, leestekens en een spatie). Elk trapezium bestaat zelf uit drie driehoeken met daarin telkens negen symbolen.

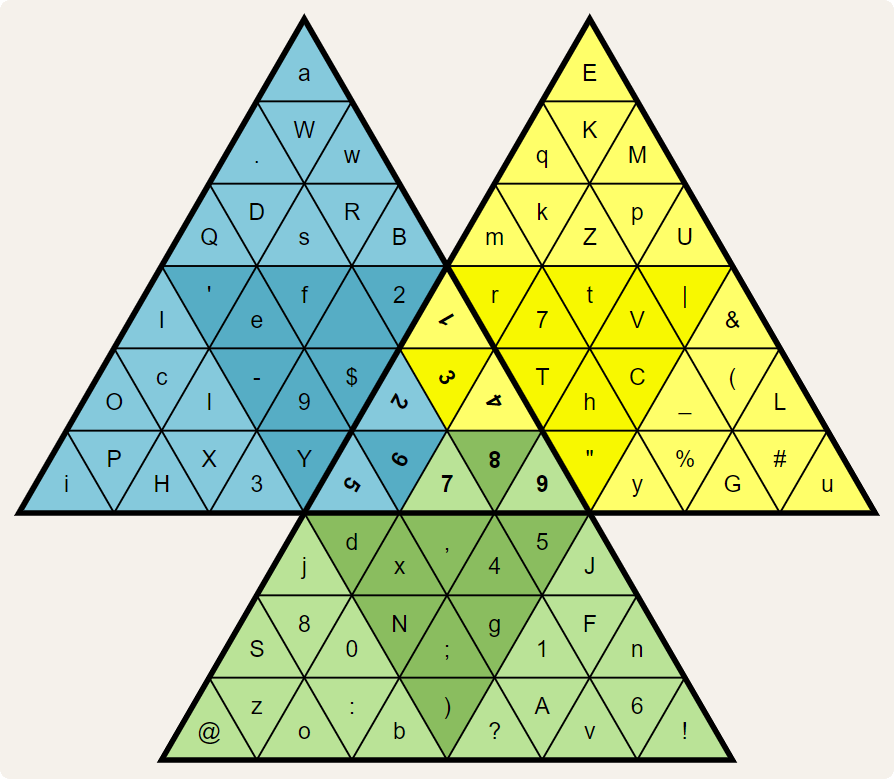
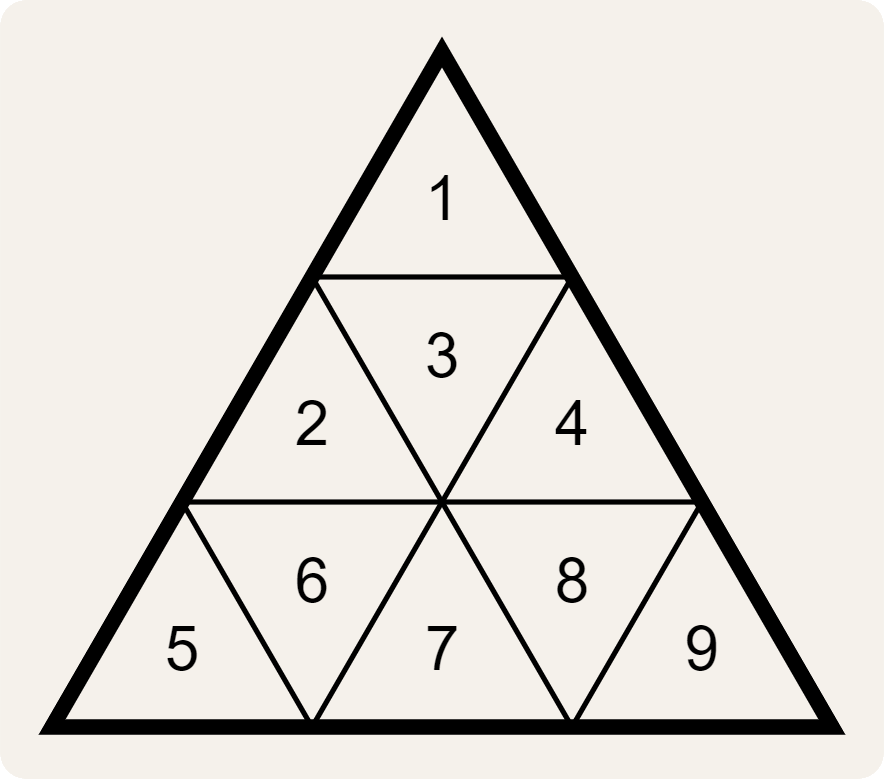
De valknut-voorstelling van een sleutel bestaat dus uit 10 driehoeken: 1 driehoek met cijfers in het midden en 9 driehoeken met symbolen die per drie samen één trapezium vormen. Elk van deze driehoeken bevat negen cijfers/symbolen. De negen cijfers/symbolen in een driehoek worden in leesvolgorde (van links naar rechts, en van boven naar onder) genummerd met de negen cijfers 1–9.

De negen cijfers/symbolen in elke driehoek van een valknut-sleutel worden in leesvolgorde (van links naar rechts, en van boven naar onder) genummerd met de negen cijfers 1–9.

Elk cijferpaar $$ij$$ ($$1 \leq i, j \leq 9$$) correspondeert dan met één symbool $$\alpha$$ dat voorkomt in één van de trapezia van de sleutel. Daarvoor zoek je het cijfer $$i$$ op in de driehoek in het midden van de sleutel. Die cijfers geven aan met welke driehoek in de trapezia het cijfer $$i$$ correspondeert. Het blauwe trapezium met de cijfers 265 binnen de driehoek in het midden is gelijkvormig aan het blauwe trapezium linksboven. De rotatie van de cijfers 2, 6 en 5 geeft aan in welke richting de driehoeken in het blauwe trapezium moeten uitgelezen worden. Op dezelfde manier corresponderen de cijfer 7, 8 en 9 met de driehoeken in het groene trapezium onderaan, en de cijfers 1, 3 en 4 met de driehoeken in het gele trapezium linksboven.

Als we gevonden hebben met welke driehoek in de trapezia cijfer $$i$$ correspondeert — en in welke richting we die driehoek moeten uitlezen — dan duidt cijfer $$j$$ het volgnummer van symbool $$\alpha$$ aan in die driehoek. Op die manier corresponderen de twee cijfers 26 met symbool W. Het eerste cijfer $$i=2$$ leidt ons naar de bovenste lichtblauwe driehoek in het blauwe trapezium. Als we die driehoek uitlezen in dezelfde richting waarin het cijfer 2 geroteerd staat in de middelste driehoek van de sleutel, dan krijgen we de reeks symbolen BwRsaW.DQ. Op positie $$j=6$$ van die reeks staat het gezochte symbool W.

De valknut-voorstelling correspondeert dus met de roostervoorstelling van een valknut-sleutel, maar vraagt wel wat meer inspanning om voor een cijferpaar het corresponderende symbool terug te vinden.