Bij het diepte-eerst doorlopen van een graaf (depth-first search, afgekort DFS) worden de toppen van een graaf \(G\) op een systematische manier doorlopen. Bij deze doorloop wordt de top die momenteel bezocht wordt, de actieve top genoemd. DFS start vanuit een bepaalde top \(r\) van \(G\), ook de wortel genoemd. De wortel is dan de eerste actieve top. Elke stap van de doorloop kan als volgt beschreven worden. Zij \(k\) de huidige actieve top in de doorloop en veronderstel dat niet alle toppen in de component van \(G\) die \(k\) bevat, reeds bezocht zijn, dan vindt één van onderstaande acties plaats.

Deze algemene stap wordt herhaald totdat elke top in deze component van \(G\) bezocht is. Wanneer niet alle toppen van \(G\) bezocht werden, dan wordt een niet-bezochte top gekozen als de volgende actieve top, waarna de doorloop verdergaat. Dit proces eindigt wanneer alle bezochte toppen actief geweest zijn.

Voorbeeld

Voorbeeld

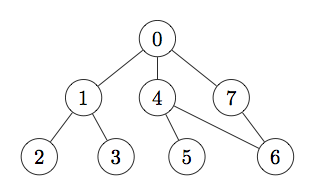
In onderstaande afbeelding wordt een DFS geïllustreerd. Er wordt hier gestart van top 0 (huidige actieve top). Vervolgens wordt een top adjacent met top 0 geselecteerd indien deze nog niet bezocht is. Hier zijn zowel top 1, top 4 en top 7 nog niet bezocht. We kiezen hier echter maar één top, bv. top 1. Deze wordt de volgende actieve top. Vervolgens wordt een top adjacent met top 1 bezocht. Ook hier zijn er meerdere mogelijkheden, maar we kiezen er één, bv. top 2. Top 2 is nu de nieuwe actieve top. Aangezien top 2 geen adjacente toppen heeft die nog niet bezocht zijn, wordt top 1 terug actief. Top 1 heeft nog één adjacente top die nog niet bezocht is, nl. top 3. Bijgevolg wordt top 3 actief. Deze heeft echter geen adjacente toppen die nog niet bezocht zijn. Bijgevolg wordt top 1 terug actief. Top 1 heeft ook geen adjacente toppen meer die nog niet bezocht zijn. Bijgevolg wordt top 0 terug actief. Analoog wordt vervolgens top 4 actief. Daarna kan top 5 actief worden, waarna terug top 4 actief wordt en vervolgens top 6 en top 7 actief kunnen worden. Bij deze DFS worden bijgevolg achtereenvolgens top 0, 1, 2, 3, 4, 5, 6 en 7 doorlopen.

Voorbeeld

In deze oefening is het de bedoeling om de volgende pseudocode te implementeren.

# De onbezochte toppen worden bijgehouden
toppen = {alle toppen}
# De oplossing wordt recursief opgebouwd.
dfs = []
Zolang er onbezochte toppen zijn:
    # Selecteer een onbezochte top
    top = een onbezochte top
    recursieDFS(top, dfs, toppen)
return dfs

recursieDFS(top, dfs, toppen)
  dfs.add(top);
  toppen.remove(top);
  Voor elke buur van top:
    Als buur in toppen:
      recursieDFS(buur, dfs, toppen);

Ontwerp en implementeer een algoritme dat een ongerichte graaf op een diepte-eerst manier doorloopt. Implementeer hiervoor een functie doorloop die als argument een ongerichte (mogelijks niet-samenhangede) graaf meekrijgt. De functie moet een lijst van toppen teruggeven in de volgorde waarin ze bij DFS doorlopen worden, startend bij een arbitraire top.

We maken bij deze oefening gebruik van een eenvoudige grafenbibliotheek graphlib. De API van de deze bibliotheek vind je hier1. Neem eerst en vooral eens de API en de bibliotheek zelf door en stel eventueel vragen hierover voor je begint te programmeren.

Belangrijke opmerking: om met de grafenbibliotheek te kunnen werken in PyCharm moet je het bestand graph_library.py2 toevoegen aan dezelfde directory als waarin je ze gebruikt. Dan kun je ze gebruiken door ze te importeren met

from graph_library import *

Dit import statement mag wel niet mee ingediend worden op dodona.

Opmerking

Het is niet toegestaan om de input van de methode doorloop aan te passen. Indien je dit wel doet, zal de test falen.

Voorbeeld

>>> DFS({0: [1, 4, 7], 1: [0, 2, 3], 2: [1], 3: [1], 4: [0, 5, 6], 5: [4], 6: [4, 7], 7: [0, 6]})
[0, 1, 2, 3, 4, 5, 6, 7]
>>> DFS({'Mike': ['Toon'], 'Toon': ['Gunnar', 'Mike'], 'Margo': ['Gunnar', 'Seppe', 'Yasmine'], 'Seppe': ['Margo'], 'Yasmine': ['Margo'], 'Gunnar': ['Margo', 'Toon']})
['Margo', 'Gunnar', 'Toon', 'Mike', 'Seppe', 'Yasmine']