Iedereen kent de methode om de nulpunten van een tweedegraadsvergelijking ($$ax^2 + bx + c = 0$$) exact te bepalen ($$\Delta = b^2 - 4 a c, \ldots$$). De berekeningen worden al een stuk ingewikkelder als men de nulpunten wil bepalen van een derde- of vierdegraadsvergelijking. Voor vergelijkingen van graad vijf of hoger bestaan er echter geen formules om de nulpunten exact te bepalen. Voor dergelijke gevallen kan zelfs bewezen¹ worden dat er geen algemene formules bestaan.

Laat je echter niet ontmoedigen omdat de wiskundig hier tekort schiet. Als de positie van de nulpunten niet exact kan bepaald worden, dan kunnen we nog altijd proberen om de positie te benaderen. Meer nog, door de beperkte nauwkeurigheid waarmee floating point getallen in een computer opgeslagen worden, is het mogelijk om nulpunten zo nauwkeurig te benaderen dat het verschil met de exacte positie kleiner wordt dan de nauwkeurigheid van de computer.

De bekendste methode om nulpunten te benaderen is de methode van Newton². Deze methode start met een initiële benadering $$x_1$$ van een nulpunt. Eenmaal een benadering $$x_n$$ ($$n = 1, 2, \ldots$$) gevonden is, kan men een nieuwe benadering $$x_{n+1}$$ bekomen die nauwkeuriger is dan de vorige door het snijpunt te bepalen van de raaklijn aan de functie in het punt $$x_n$$ met de $$X$$-as. Deze procedure kan men blijven herhalen, totdat uiteindelijk een benadering bekomen wordt die voldoende nauwkeurig is.

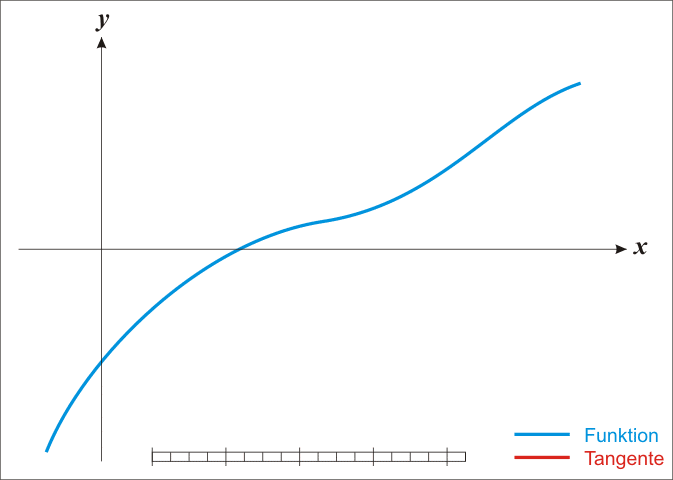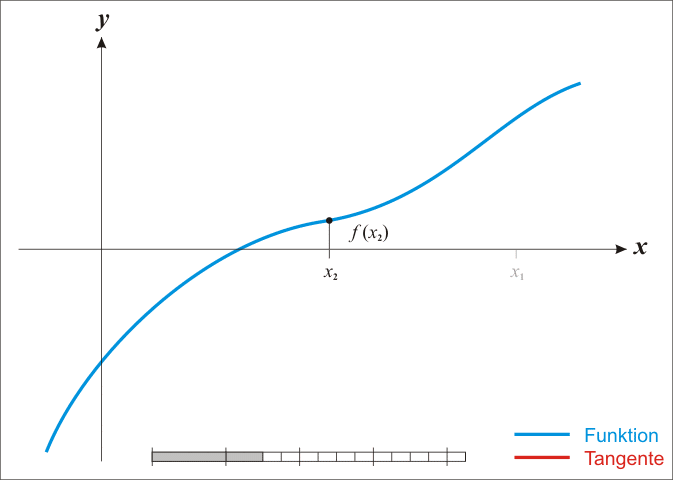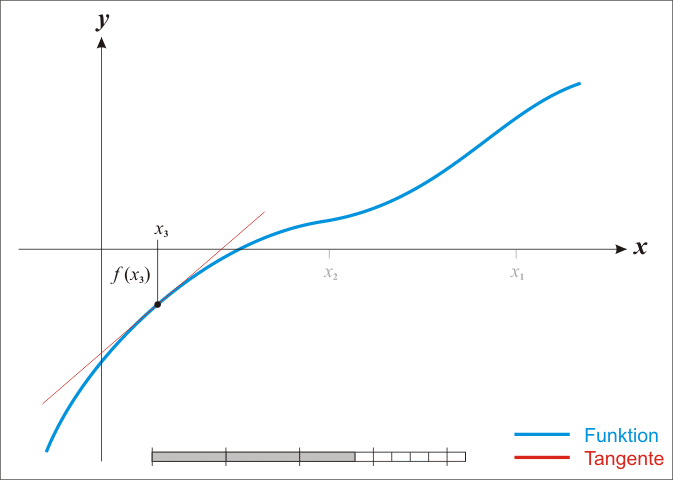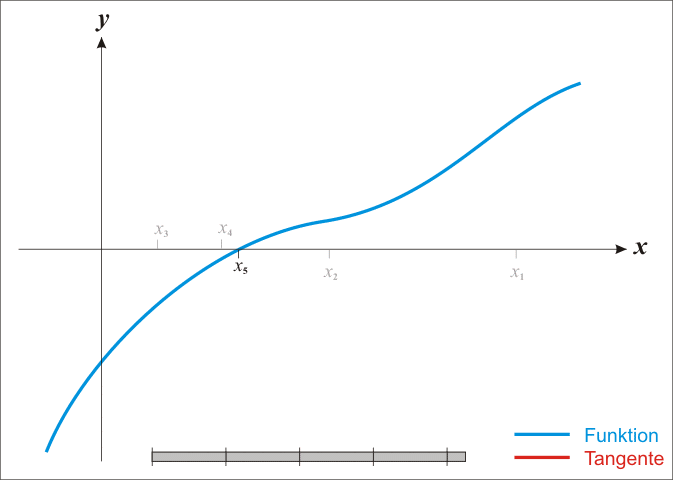
Indien een benadering $$x_n$$ gekend is, dan kan de volgende benadering bepaald worden als $$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$. Hierbij stelt $$f'$$ de afgeleide van de functie $$f$$ voor, zodat $$f'(x)$$ de richtingscoëfficiënt oplevert van de raaklijn aan de functie $$f$$ in het punt $$x$$. Om een goede benadering te kunnen vinden aan de hand van de methode van Newton, is het van belang om een initiële schatting $$x_1$$ te hebben die voldoende dicht bij het nulpunt gelegen is (hoe dicht hangt af van de functie zelf). De reeks benaderingen kan dan voortgezet worden totdat $$f(x_m)$$ voldoende dicht bij nul ligt.

Opgave

De Vanderwaalskracht³ $$E$$ tussen twee atomen in een inert gas kan geschreven worden in functie van de afstand $$r$$ van de atomen \[E(r) = \frac{A}{r^{12}} - \frac{B}{r^6}\] waarbij $$A$$ en $$B$$ twee gasconstanten zijn die experimenteel moeten bepaald worden. Voor deze opgave moet je de methode van Newton toepassen om de afstand tussen twee atomen te vinden waarbij $$E = 100$$. Je moet met andere woorden een nulpunt zoeken van de functie $$f(r) = E(r) - 100$$. We geven nog de afgeleide van deze functie mee: \[f'(r) = -\frac{12 A}{r^{13}} + \frac{6 B}{r^7}\]

Invoer

De invoer bestaat uit drie reële getallen, elk op een afzonderlijke regel. De eerste twee regels bevatten de experimenteel bepaalde waarden van de gasconstanten $$A$$ en $$B$$. De derde regel bevat een initiële benadering $$r_1$$ van een afstand waarvoor $$E(r_1) \approx 100$$.

Uitvoer

De eerste benadering $$r_m$$ die gevonden wordt op basis van de methode van Newton waarvoor $$|E(r_m) - 100| \le \epsilon$$, waarbij $$\epsilon = 10^{-8}$$. Deze benadering is dus nauwkeurig tot op acht cijfers na de komma.

Voorbeeld

Invoer:

1.5
7.12
0.5

Uitvoer:

0.6718209666720478