Gegeven een reeks punten in het vlak $$(x_0, y_0)$$, $$(x_1, y_1)$$, ..., $$(x_N, y_N)$$. Indien we een verband vermoeden $$y = f(x)$$, bestaan verschillende algoritmen om een dergelijke functie $$f(x)$$ te bepalen. Een dergelijke functie wordt een interpolatie-functie genoemd, omdat ze het mogelijk maakt ook $$y$$-waarden in tussenliggende $$x$$-waarden te bepalen.
We kunnen steeds een veelterm van graad $$N$$ construeren, een zogenaamde Lagrange-veelterm, die door alle punten $$(x_i, y_i)$$ ($$0 \le i \le N$$) gaat. Dit is een veelterm van graad $$N$$, gedefinieerd door:

$$ p(x) = \sum_{i = 0}^N y_i L_i(x) $$

met

$$ L_i(x) = \prod_{j = 0, j \neq i}^N \frac{x - x_j}{x_i - x_j} $$

Men ziet inderdaad gemakkelijk in dat $$L_i(x_k) = 0$$ voor $$i \neq k$$ en $$L_i(x_i) = 1$$.

Hieronder worden enkele voorbeelden getoond van Lagrange-veeltermfuncties voor resp. 2, 3, 4 en 5 gegeven punten.

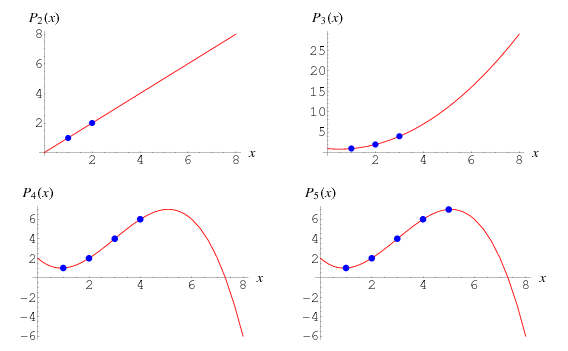
(bron: mathworld.wolfram.com/LagrangeInterpolatingPolynomial.html)

Schrijf een functieklasse LagrangePolynoom met:

• een constructor die een lijst van $$M$$ tuples $$(x_i, y_i)$$ bevat ($$M > 0$$) (Bemerk dat voor de formules hierboven weergegeven geldt $$M = N+1$$.)
• een methode value() bevat, met 1 argument, die als resultaat de functiewaarde in dit argument van de Lagrangeveelterm oplevert.

Voorbeeld

p1 = LagrangePolynoom([(1.0, 2.0), (3.0, 5.0), (7.0, 12.0)])
p1.value(1.0) = 2.0
p1.value(3.0) = 5.0
p1.value(7.0) = 12.0
p1.value(2.0) = 3.4583333333333335
p1.value(5.0) = 8.333333333333332

p2 = LagrangePolynoom([(1.0, -1.0), (2.0, 12.0), (-1.0, -15.0), (-2.0, -40.)])
p2.value(1.0) = -1.0
p2.value(2.0) = 12.0
p2.value(-1.0) = -15.0
p2.value(-2.0) = -40.0
p2.value(0.0) = -6.0
p2.value(3.0) = 45.0